二项分布的理论基础应用及Python实践
Posted Python圈子
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二项分布的理论基础应用及Python实践相关的知识,希望对你有一定的参考价值。
二项分布是概率统计中非常基础、非常实用的一种分布,可以说它在我们的生活中无所不在。它说明了这样一种现象:在给定的试验次数中,某一结果会发生多少次。
比如:
这个月有多少天会刮北风?
今年有多少天会下雨?
经过一个路口100次,有多少次会是绿灯?
一年之中会有多少次出门就见狗?
伯努利分布是二项分布的基础,它只有两种状态,比如抛硬币的时候,结果只有正面和反面两种情况,且两种情况的概率之和为1。也就是说,当我们给定正面朝上的概率的时候,这个分布的一切就都确定了。
我们以0和1来标识这两种可能的结果,那么其概率函数为:
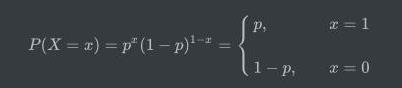
那么其期望值为:
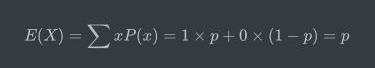
其方差为:
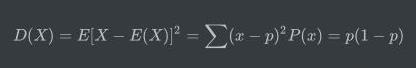
1. 排列
从n个对象中有序地挑选出r个对象,我们称之为排列,我们用以下公式统计其可能产生的排列数:
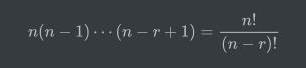
2. 组合
考虑另一种情况,仍然是从n个对象中抽取r个对象,但是这次我们不考虑其顺序,这种过程我们称之为组合。我们用以下公式统计其可能产生的组合数:
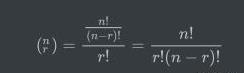
可以看出,这是n选r的排列数除以r的排列数。上述公式又被称作二项系数,通常用“n选r”表示。
3. Python计算
那么接下来我们用Python来写一个函数,用来计算不同参数下的排列与组合的数量。在排列组合的计算中,我们可能会输入两个参数:总样本量n、需要抽取的样本数k。
那么我们就定义如下函数:
from functools import reducedef PC(n, k):"""计算并返回排列组合数"""# 非法输入返回空if n <= 0 or k < 0 or n < k:print('Wrong Input!')return None# k为0时,排列组合的情况恒为1if k == 0:return 1, 1# 生成正序及倒序的序列series_asc = list(range(1, n+1))series_desc = sorted(series_asc, reverse=True)# 排列permutation = reduce(lambda x, y: x*y, series_desc[:k])# 组合perm2 = reduce(lambda x, y: x*y, series_asc[:k])combination = int(permutation / perm2)return permutation, combination
随手测试几个:
for n in range(1, 5):for k in range(1, 3):print('-'*10)print(n, k)print(PC(n, k))
结果是正确的:
----------1 11)----------1 2Wrong Input!None----------2 12)----------2 21)----------3 13)----------3 23)----------4 14)----------4 26)
回顾伯努利分布的情况:一次实验只有可能有两种结果,分别用0和1来表示,其中结果1发生的概率为p。那么在n次独立实验中,不考虑顺序的情况下,结果1出现k次的概率是多少?
首先,因为n次实验相互独立,所以根据乘法定律,任何一种结果1出现k次的场景发生的概率均为:
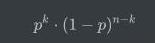
然后,我们需要考虑结果为1的次数刚好为k的情况有多少种。很明显,这就是一个伯努利试验的组合问题,n次实验中有k次结果为1的情况共有“n选k”种,两者相乘就是该事件发生的概率。
因此:
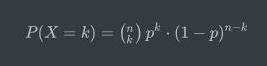
那么我们来用Python实现一个计算二项分布概率的小工具,在这里,我们的输入参数包含总试验次数n、正样本发生的次数k以及正样本发生的概率p:
def binominal_prob(n, k, p):"""计算并返回二项分布中某结果发生的概率"""# 任一k次成功的序列出现的概率p_base = p ** k * (1-p) ** (n-k)# n次试验中k次成功的组合数# 直接用上边我们编写的排列组合函数来求解combination = PC(n, k)[1]p_result = p_base * combinationreturn p_result
那么接下来,我们利用我们刚刚写好的小工具,来看一下在10次试验中,不同的概率对应的二项分布是什么样的。
probs = [binominal_prob(10, i, 0.5) for i in range(11)]我们将结果画出来看看:
%matplotlib inlineimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snssns.set()probs = [round(i/10,1) for i in range(1, 10)]n = 20plt.figure(figsize=(16, 6))for p in probs:dist_probs = [binominal_prob(n, i, p) for i in range(n+1)]plt.plot(range(n+1), dist_probs, label='p={0}'.format(p))plt.legend()plt.title('Binominal Distributions of Different P value')plt.savefig('binominal.jpg')plt.show()
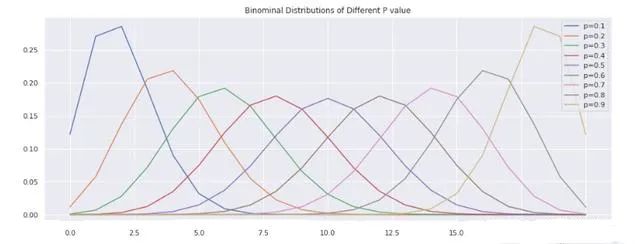
或者我们使用交互式的绘图库plotly来尝试同样的事情:
import plotly.graph_objects as goprobs = [round(i/10,1) for i in range(1, 10)]n = 20fig = go.Figure()for p in probs:dist_probs = [binominal_prob(n, i, p) for i in range(n+1)]fig.add_trace(go.Scatter(x=list(range(n+1)),y=dist_probs,name='p={0}'.format(p)))fig.show()
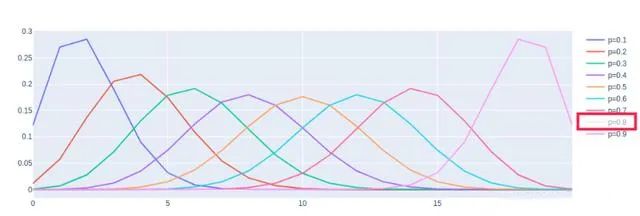
可以看到,plotly实现的效果更加靓丽,且额外支持了动态交互,在这里我就选择把p=0.8这条线隐藏了起来。
我们现在想象一种情况,有一枚分布不太均匀的硬币,每次抛向空中后,落地为正面的概率为p,任意两次实验之间相互独立。现在我们做了4次实验,其中有三次正面朝上,那么请问p的值为多少?
我们之前曾经提到过极大似然估计,在这里我们用同样的思路去估计p的取值。极大似然估计的思想就是寻找一个参数,使得当前结果发生的概率最大,那么我们先定义出来当前结果发生的概率公式:
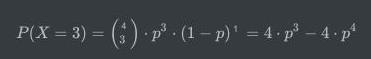
对其求导并使导数为0,有:

可得,当p=0.75时,P(X=3)=0.422达到最大(另一个解p=0显然不可能,因为硬币朝上已经发生了,并不是“不可能事件”;另外考虑不同区间导数的取值也可以得到答案)。
- END -
文源网络,仅供学习之用,如有侵权,联系删除。
◆
◆
◆
◆
◆
以上是关于二项分布的理论基础应用及Python实践的主要内容,如果未能解决你的问题,请参考以下文章