聚类算法中的四种距离及其python实现

Posted 2021-04-06 Hill的数据分析成长之路

欧氏距离

    欧式距离也就是欧几里得距离，是最常见也是最简单的一种距离，再n维空间下的公式为：

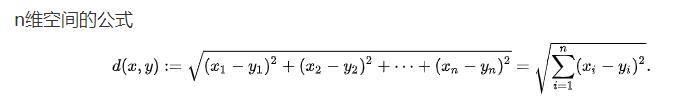
    在python中，可以运用scipy.spatial.distance中的pdist方法来实现，但需要调整其中参数为metric='euclidean'，具体代码如下：

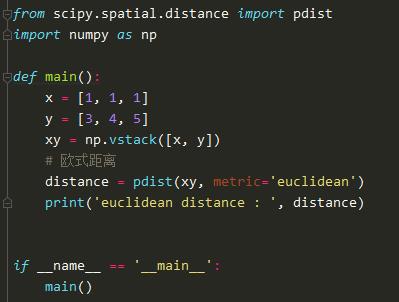
    运行程序之后结果如下：

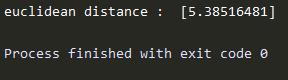
曼哈顿距离

    曼哈顿距离顾名思义，来自于计算城市的道路距离，由于实际城市中由一点到达另外一点的通过方式要通过道路来到达，此时两点间的距离不能直接使用欧式距离来计算（车辆行驶过程中不能穿越房屋），因此催生出曼哈顿距离。用数学语言描述就是使用再集合度量空间的几何学用语，用以表明两点在标准坐标系上的绝对轴距总和。

    在python中，可以运用scipy.spatial.distance中的pdist方法来实现，但需要调整其中参数为metric='cityblock'，具体代码如下：

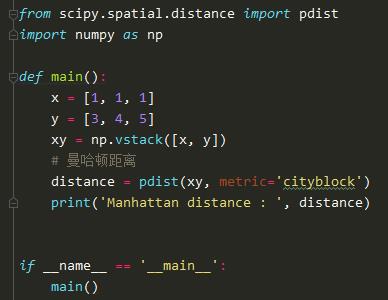
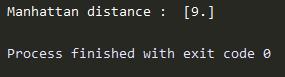
    运行程序之后结果如下：

切比雪夫距离

    切比雪夫距离是向量空间中的一种度量，两点之间的距离定义是其各坐标数值插值绝对值的最大值。切比雪夫距离用公式比较好理解，公式如下：

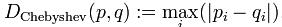
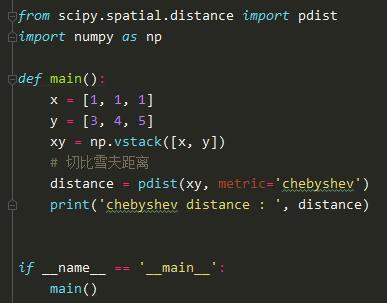
    在python中，可以运用scipy.spatial.distance中的pdist方法来实现，但需要调整其中参数为metric='chebyshev'，具体代码如下：

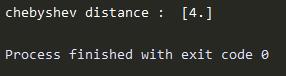
   运行程序之后结果如下：

闵可夫斯基距离

    闵可夫斯基距离不是一个距离，而是一组距离的定义，n维空间中的闵式距离公式如下：

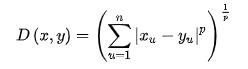
    由公式可以看出，上述三种距离是闵式距离的特殊情况：

    当p = 1时，上式是曼哈顿距离

    当p = 2时，上式是欧氏距离

    当p→∞时，上式是切比雪夫距离

    根据参数的同步，闵式距离可以表示一类的距离。

   在python中，可以运用scipy.spatial.distance中的pdist方法来实现，但需要调整其中参数为metric='minkowski'，p=4.（默认是p=2，是欧氏距离），具体代码如下：

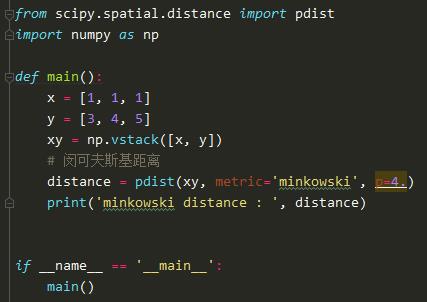
   运行程序之后结果如下：

    综上四种距离是聚类算法中常用的四类距离，各有各的特色，在不同环境下选择合适的距离最为恰当~