机器学习基础数学推导+纯Python实现机器学习算法17：XGBoost

Posted 2021-04-06 机器学习初学者

Python机器学习算法实现

Author：louwill

Machine Learning Lab

     

     自从陈天奇于2015年提出XGBoost以来，该模型就一直在各大数据竞赛中当作大杀器被频繁祭出。速度快、效果好是XGBoost的最大优点。XGBoost与GBDT同出一脉，都属于boosting集成学习算法，但XGBoost相较于GBDT要青出于蓝而胜于蓝。

     XGBoost的全程为eXtreme Gradient Boosting，即极端梯度提升树。要深入理解整个XGBoost模型系统，建议还是要认真研读陈天奇的 XGBoost: A Scalable Tree Boosting System 论文，深入损失函数的推导，这样才能更好的掌握XGBoost。本文仅对模型最重要的部分，即XGBoost损失函数的数学推导过程和结点分裂的增益计算方式进行阐述。

XGBoost原理推导

     既然XGBoost整体上仍然属于GBDT系统，那么XGBoost也一定是由多个基模型组成的一个加法模型，所以XGBoost可表示为：

     假设 第   次迭代要训练的树模型是   ，可得：

     下面进入正题，推导XGBoost损失函数：

     损失函数原始形式可表示为：

     其中，   为损失函数的正则化项，表示全部   棵树的复杂度之和，旨在防止模型过拟合。

     XGBoost来自于GBDT，同样也适用前向分步算法，以第   步的模型为例，模型对第   个样本   的预测值为：

     其中，   是由第     步的模型给出的预测值，作为一个已知常数存在，     是第   步树模型的预测值。所以，目标函数可以改写为：

     同时也可以对正则化项进行拆分，由于前  棵树的结构已经确定，因此前    棵树的复杂度之和也可以表示为常数：

     然后我们使用二阶泰勒公式(这里需要大家回顾微积分相关知识)，可以将损失函数改写为：

     其中，   为损失函数的一阶导，   为损失函数的二阶导，需要注意的是这里是对   求导。XGBoost相较于GBDT而言用到了二阶导数信息，所以如果要自定义损失函数，首要的要求是其二阶可导。

     以平方损失函数为例：

     则有：

     将该二阶泰勒展开式带入前述推导的XGBoost损失函数中，可得损失函数的近似表达式：

     对上式去除相关常数项，简化后的损失函数为：

     所以只需要求出每一步损失函数的一阶导和二阶导的值，然后最优化目标函数，就可以得到每一步的   ，最后根据加法模型得到一个boosting模型。

     然后重新定义一棵决策树，其包括两个部分：叶子结点的权重向量   和实例(样本)到叶子结点的映射关系   (本质是树的分支结构)；

     所以一颗树的数学表达为：

     再来看定义模型复杂度的正则化项。模型复杂度   可由单棵树的叶子结点数     和叶子权重     ，具体来说损失函数的复杂度由所有树的叶子结点数和叶子权重所决定。数学表达如下式所示：

     然后我们对所有叶子结点进行重新归组。将属于第   个叶子结点的所有样本   划入到一个叶子结点的样本集合中，即：   ，从而XGBoost的目标函数可以改写为：

定义   ，   简化一下表达，含义如下：

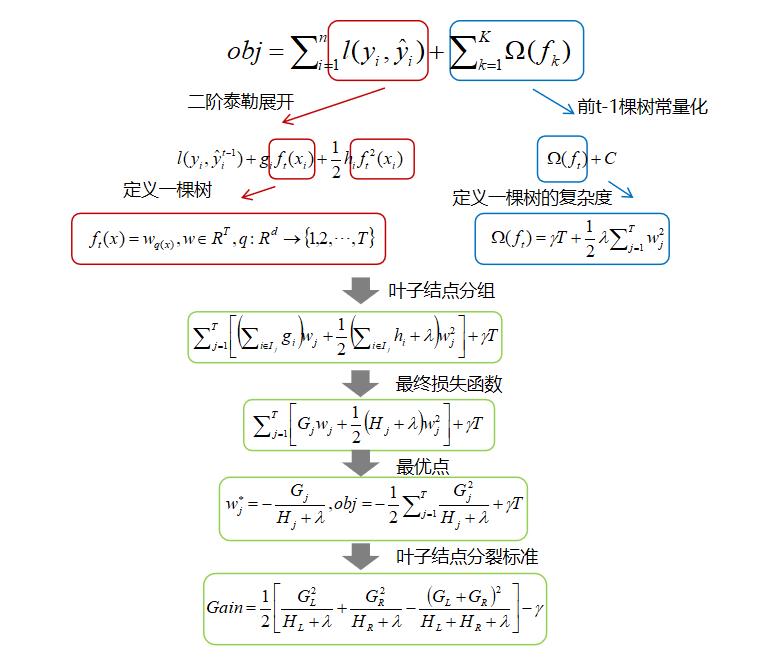
•  ：叶子结点     所包含样本的一阶偏导数累加之和，是一个常量；
•  ：叶子结点     所包含样本的二阶偏导数累加之和，是一个常量；

将   和   带入前述XGBoost损失函数，可得最终的损失函数表达式为：

根据一元二次方程的求解公式，可得：

代入到XGBoost的最终损失函数，可得损失为：

对于每个叶子结点    将其从目标函数中拆解出来，有:

     由前述推导可知，   和   相对于第   棵树来说是可以计算出来的。所以该式就是一个只包含一个变量叶子结点权重   的一元二次函数，可根据最值公式求其最值点。当相互独立的每棵树的叶子结点都达到最优值时，整个损失函数也相应的达到最优。

     当树结构固定的情况下，对上式求导并令其为0，可得最优点和最优值为：

     以上就是XGBoost完整的损失函数推导过程。基本框架仍然是GBDT框架，但XGBoost的最大特色是用到了损失函数的二阶导数信息，目的就在于能够更加准确的逼近真实损失。

     下图是XGBoost论文中给出的叶子结点权重计算：

     根据二阶导信息把XGBoost的优化推到了极为逼近真实损失的状态，其结点分裂方式就跟CART树的结点分裂方式本质上并没有太大区别，但信息增益的计算方式有所不同。

     假设模型在某一节点完成特征分裂，分裂前的目标函数可以写为：

     分裂后的目标函数为：

     则对于目标函数来说，分裂后的收益为：

     如果增益Gain>0，即分裂为两个叶子节点后，目标函数下降了，则考虑此次分裂的结果。实际处理时需要遍历所有特征寻找最佳分裂特征。

     以上就是XGBoost模型核心数学推导部分。完整的XGBoost模型还有很多工程上的细节，这里不做过多阐述，各位读者最好把XGBoost论文认真研读一遍。完整的XGBoost推导示意图如下所示。

XGBoost算法实现

     有了GBDT的算法实现经验，XGBoost实现起来就并没有太多困难了，大多数底层代码都较为类似，主要是在信息增益计算、叶子得分计算和损失函数的二阶导信息上做一些变动。同样先列出代码框架：

     底层的决策树结点和树模型定义基本差别不大，具体这里不再列出，可参考第15讲GBDT实现方式。主要是继承底层的树结点和树来定义XGBoost单棵树和XGBoost树模型拟合方式。

     定义XGBoost单棵树模型如下：

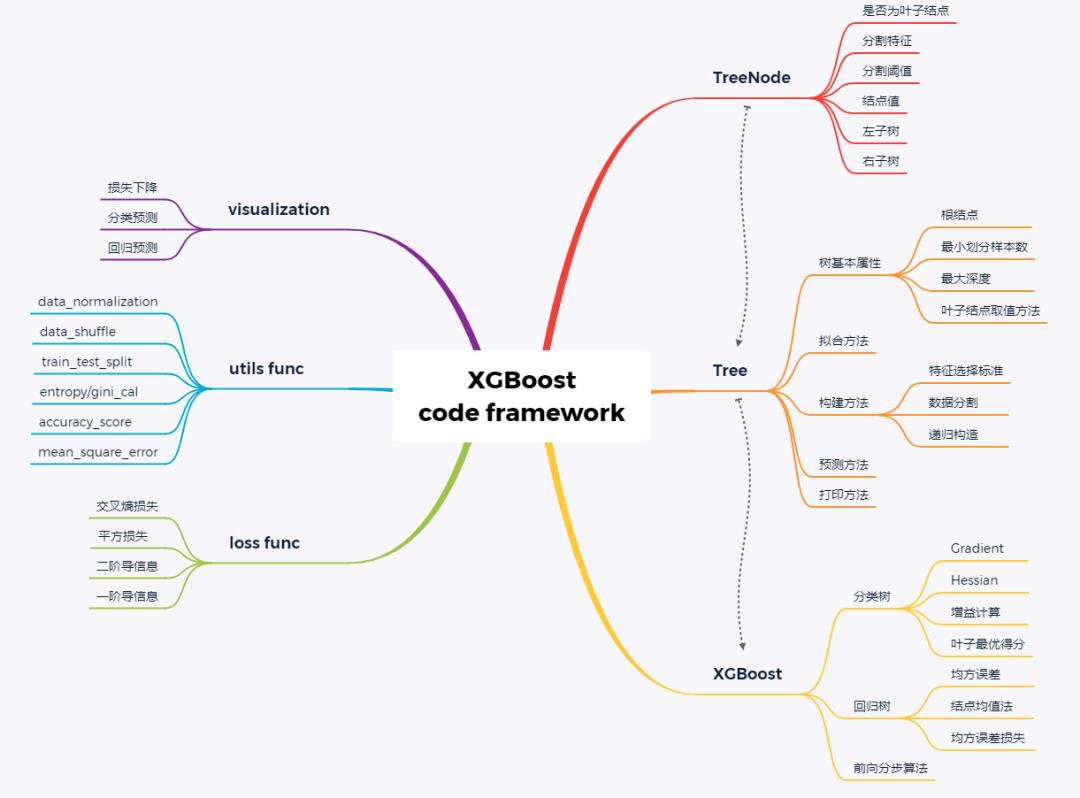
class XGBoostTree(Tree): # 结点分裂 def _split(self, y): col = int(np.shape(y)[1]/2) y, y_pred = y[:, :col], y[:, col:] return y, y_pred
 # 信息增益计算公式 def _gain(self, y, y_pred): Gradient = np.power((y * self.loss.gradient(y, y_pred)).sum(), 2) Hessian = self.loss.hess(y, y_pred).sum() return 0.5 * (Gradient / Hessian)
 # 树分裂增益计算 def _gain_by_taylor(self, y, y1, y2): # 结点分裂 y, y_pred = self._split(y) y1, y1_pred = self._split(y1) y2, y2_pred = self._split(y2)
 true_gain = self._gain(y1, y1_pred) false_gain = self._gain(y2, y2_pred) gain = self._gain(y, y_pred) return true_gain + false_gain - gain
 # 叶子结点最优权重 def _approximate_update(self, y): # y split into y, y_pred y, y_pred = self._split(y) # Newton's Method gradient = np.sum(y * self.loss.gradient(y, y_pred), axis=0) hessian = np.sum(self.loss.hess(y, y_pred), axis=0) update_approximation = gradient / hessian
 return update_approximation
 # 树拟合方法 def fit(self, X, y): self._impurity_calculation = self._gain_by_taylor self._leaf_value_calculation = self._approximate_update super(XGBoostTree, self).fit(X, y)

     然后根据前向分步算法定义XGBoost模型：

class XGBoost(object):
 def __init__(self, n_estimators=200, learning_rate=0.001, min_samples_split=2, min_impurity=1e-7, max_depth=2): self.n_estimators = n_estimators # Number of trees self.learning_rate = learning_rate # Step size for weight update self.min_samples_split = min_samples_split # The minimum n of sampels to justify split self.min_impurity = min_impurity # Minimum variance reduction to continue self.max_depth = max_depth # Maximum depth for tree

 # 交叉熵损失 self.loss = LogisticLoss()
 # 初始化模型 self.estimators = [] # 前向分步训练 for _ in range(n_estimators): tree = XGBoostTree( min_samples_split=self.min_samples_split, min_impurity=min_impurity, max_depth=self.max_depth, loss=self.loss)
 self.estimators.append(tree)
 def fit(self, X, y): y = to_categorical(y)
 y_pred = np.zeros(np.shape(y))        for i in range(self.n_estimators): tree = self.trees[i] y_and_pred = np.concatenate((y, y_pred), axis=1) tree.fit(X, y_and_pred)            update_pred = tree.predict(X) y_pred -= np.multiply(self.learning_rate, update_pred)
 def predict(self, X): y_pred = None # 预测 for tree in self.estimators: update_pred = tree.predict(X) if y_pred is None: y_pred = np.zeros_like(update_pred) y_pred -= np.multiply(self.learning_rate, update_pred)
 y_pred = np.exp(y_pred) / np.sum(np.exp(y_pred), axis=1, keepdims=True) # 将概率预测转换为标签 y_pred = np.argmax(y_pred, axis=1) return y_pred

     使用sklearn数据作为示例：

from sklearn import datasetsdata = datasets.load_iris()X = data.datay = data.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, seed=2)  
clf = XGBoost()clf.fit(X_train, y_train)y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)print ("Accuracy:", accuracy)

Accuracy: 0.9666666666666667

     XGBoost也提供了原生的模型库可供我们调用。pip安装xgboost即可：

pip install xgboost

     同样使用sklearn数据集进行测试：

import xgboost as xgbfrom xgboost import plot_importancefrom matplotlib import pyplot as plt
# 设置模型参数params = { 'booster': 'gbtree', 'objective': 'multi:softmax',  'num_class': 3,  'gamma': 0.1, 'max_depth': 2, 'lambda': 2, 'subsample': 0.7, 'colsample_bytree': 0.7, 'min_child_weight': 3, 'silent': 1, 'eta': 0.001, 'seed': 1000, 'nthread': 4,}
plst = params.items()
dtrain = xgb.DMatrix(X_train, y_train)num_rounds = 200model = xgb.train(plst, dtrain, num_rounds)
# 对测试集进行预测dtest = xgb.DMatrix(X_test)y_pred = model.predict(dtest)
# 计算准确率accuracy = accuracy_score(y_test, y_pred)print ("Accuracy:", accuracy)# 绘制特征重要性plot_importance(model)plt.show();

Accuracy: 0.9166666666666666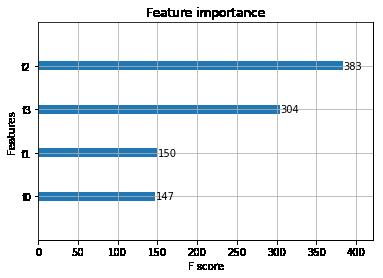

参考资料：

XGBoost: A Scalable Tree Boosting System

https://www.jianshu.com/p/ac1c12f3fba1

往期精彩：

和线性支持向量机

   
     
     
   

    
      
      
    
 
     
 
      
 
       
 
        
 
         
 
          
 
           
往期精彩回顾
 
          
 
         
 
        
 
       
 
      
 
     
 
    
   
     
     
   
   
     
     
   

    
      
      
    
 
     
 
      
 
       
 
      
 
      
 
       
 
        
 
       
 
       
 
        
 
       
 
      
 
      
 
       
 
      
 
     
 
     
 
      
 
      
 
      
 
      
 
      

 
      
 
      
 
     
 
     
获取一折本站知识星球优惠券，复制链接直接打开：
 
     
https://t.zsxq.com/yFQV7am
 
     
本站qq群1003271085。
 
     
加入微信群请扫码进群：