《机器学习实战》之K均值聚类--基于Python3

Posted 2021-04-06 华少的知识宝典

之前学习的算法都是有监督学习，而聚类是一种无监督的学习方法。所谓无监督学习是指事先并不知道要寻找的内容。聚类将数据点归到多个簇中，其中相似数据点处于同一簇，而不相似数据点处于不同簇。K均值（K-means）算法是一种广泛使用的聚类算法，其中k是用户指定的要创建的簇的数目。

K  -  均  值  聚  类

1、K-means原理      

聚类是一种无监督学习，它将相似的对象归到同一个簇中，簇内的对象越相似，聚类的效果越好。K均值聚类（K-means）是一种简单的无监督学习算法，其可以发现k个不同的簇，且每个簇的中心采用簇中所含值的均值计算而成。

簇 与 质心：KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇，直观上来看，簇是一组一组聚集在一起的数据，在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。  簇中所有数据的均值通常被称为这个簇的“质心”（centroids）。在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。

K均值算法的工作流程为，首先根据用户给定的簇的个数k来随机确定k个初始点作为质心。然后，为数据集中的每一个点寻找距离其最近的质心，并将其分配给该质心所对应的簇。之后，再将每个簇的质心更新为该簇所有点的平均值。不断迭代该过程，当所有数据点的分配结果不再变化时，停止迭代。

该过程用伪代码可表示为：

创建k个点作为起始质心（通常是随机选择）当任意一个点的簇分类结果发生变化时 对数据集中的每一个数据点 对每个质心 计算质心与数据点之间的距离 将数据点分配到距其最近的簇    对每一个簇，计算簇中所有点的均值作为质心

    

2、距离的测度         

在k均值算法中，需要寻找最近的质心，也就是说要进行某种距离的计算。

3、代码实现         

了解了上面的这些东西后，差不多就能够实现kMeans了。

3.1 获取数据

最开始当然是导入模块和获取数据了。数据在testSet.txt文件中，样式如下：

from numpy import *import matplotlib.pyplot as plt
"""函数说明: 加载数据集
Parameters: fileName - 文件名Returns: dataMat - 数据矩阵，list类型"""def loadDataSet(fileName): dataMat = [] fr = open(fileName) for line in fr.readlines(): curLine = line.strip().split('	') fltLine = list(map(float,curLine)) # 将每行的内容映射成浮点数，这里是避免数据文本中有整数 dataMat.append(fltLine) return dataMat

我们可以提前看一看这些数据：

dataMat = loadDataSet("testSet.txt")plt.scatter(array(dataMat)[: ,0],array(dataMat)[: ,1])plt.show()

其实在这里我们可以猜测，数据应该会被分为4簇。

3.2 辅助函数

接下来定义两个辅助函数，用于后面的kMeans算法。

"""函数说明: 计算两个向量的欧氏距离
Parameters: vecA - 向量A vecB - 向量BReturns: 欧氏距离"""def distEclud(vecA, vecB): return sqrt(sum(power(vecA - vecB, 2))) # 平方和开根号
"""函数说明: 为给定数据集构建一个包含k个随机质心的集合
Parameters: dataSet - 给定的数据集 k - 随机质心的个数Returns: centroids - 包含k个随机质心的集合"""def randCent(dataSet, k): n = shape(dataSet)[1] # 获得数据集的 列数，也就是特征个数 centroids = mat(zeros((k,n))) # 产生一个 k*n 的 矩阵 for j in range(n): # 遍历数据集的每一列。二维数据时，也就相当于坐标的 x轴 和 y轴 minJ = min(dataSet[:,j]) # 获得这一列上的 最小值  rangeJ = float(max(dataSet[:,j]) - minJ) # 取值范围--这一列 最大值与最小值之间的差值 centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1)) # 产生 随机质心 return centroids

试验一下我们的randCent函数，该函数用来产生初始的随机质心。

因为随机质心必须在整个数据集的边界之内，所以通过找到数据集每一维上的最小值和最大值来完成。然后通过产生0到1之间的随机数，并通过取值范围和最小值，确保随机点在数据边界之内。

print("第一列最小值为：", min(array(dataMat)[: ,0])) # 这里要使用array函数将list类型数据转换一下，否则会报错print("第一列最大值为：", max(array(dataMat)[: ,0]))print("第二列最小值为：", min(array(dataMat)[: ,1]))print("第二列最大值为：", max(array(dataMat)[: ,1]))
centroids = randCent(array(dataMat),2) # 产生两个随机质心print(centroids)

可以看到，产生的随机质心符合要求。

3.3 k均值算法

接下来主角登场，k均值算法来了。

"""函数说明: k-均值聚类算法
Parameters: dataSet - 给定的数据集 k - 簇的个数（要想分出几个簇，就需要有几个质心） distMeas - 计算距离的方法，默认使用欧氏距离 createCent - 创建初始质心的方法，默认为在数据范围内随机生成Returns: centroids - 所有的类质心 clusterAssment - 点分配结果。存储每个点的簇分配结果的矩阵，第一列记录簇索引值，第二列存储误差（当前点到簇质心的距离的平方值）""" def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent): m = shape(dataSet)[0] # 获得数据集的 行数，也就是 数据点 的个数 clusterAssment = mat(zeros((m,2))) # 创建一个 m*2 的矩阵,存储点分类结果。每一行的结果对应数据集的每一行 centroids = createCent(dataSet, k) # 产生随机质心 clusterChanged = True # 是否继续迭代的标志变量  # 遍历所有数据点，计算质心，分配簇 while clusterChanged: clusterChanged = False for i in range(m): # 遍历数据集的每一行 minDist = inf # 初始化最小距离为 无穷大。inf表示无穷大 minIndex = -1 # 初始化最小索引 # 寻找最近的质心 for j in range(k): # 遍历质心 distJI = distMeas(centroids[j,:],dataSet[i,:]) # 计算每个 质心 与 数据点 的距离 if distJI < minDist: minDist = distJI; minIndex = j  if clusterAssment[i,0] != minIndex: # 簇分配仍然发生了变化 clusterChanged = True # 继续迭代 clusterAssment[i,:] = minIndex,minDist**2 # 更新簇分配的结果。第一列记录 簇索引值，第二列 存储误差（当前点到簇质心的距离的平方值） print("质心为：
", centroids)  # 更新质心 for cent in range(k): '''  几个函数的介绍： 矩阵.A：把 矩阵 转换为 数组numpy nonzero()：返回哪些元素不是False或者0 下面这行代码的逻辑可以看个，按着里面的顺序一步步执行就好了（为了演示，里面把cent设为了1）： https://blog.csdn.net/xinjieyuan/article/details/81477120 ''' ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]  centroids[cent,:] = mean(ptsInClust, axis=0) # 沿矩阵的列方向（axis=0） 计算该簇所有点的均值 return centroids, clusterAssment

逻辑比较简单，参考上面的 第一节 K-means原理。

用这个函数来试试对数据集的聚类吧。这里，我们按照先前的猜测，设置簇的个数为4，并将数据以散点图的形式画出来，将不同的簇用不同的颜色标记，质心以十字形的标记显示。

myCentroids,clusterAssing = kMeans(array(dataMat),4)
print(array(clusterAssing)[:,0]) # 所有数据的簇索引 plt.scatter(array(dataMat)[: ,0],array(dataMat)[: ,1],c=array(clusterAssing)[:,0]) # 画出数据散点图，属于相同索引的用同一个颜色plt.scatter(array(myCentroids)[:,0],array(myCentroids)[:,1],marker="+",s=200,c="red") # 画出 簇中心plt.show()

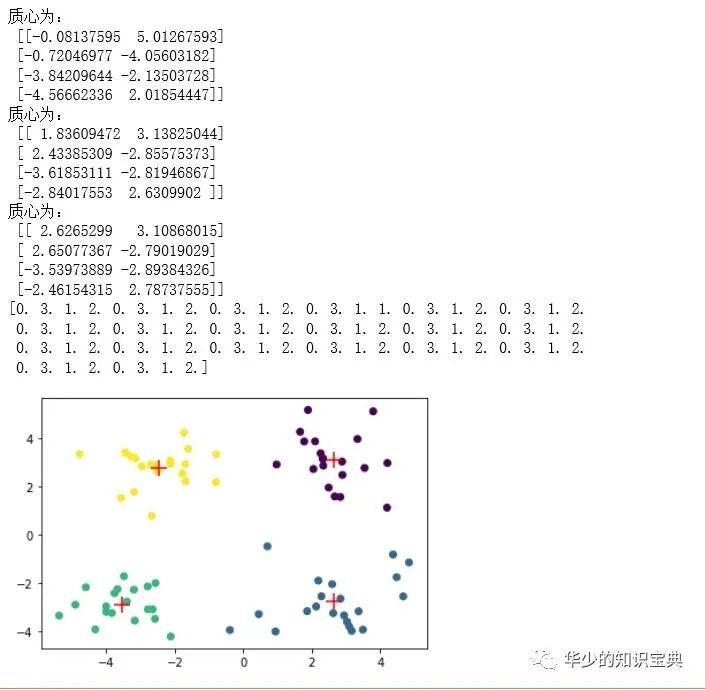
可以看到，程序一共迭代了三次，最后得到了最终的质心。

4、二分K-均值算法     

二分K-均值算法是对上面的k-均值算法的改进，克服了k-均值算法收敛于局部最小值的问题。其首先将所有点作为一个簇，然后将该簇一分为二，之后选择其中一个簇继续划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE（误差平方和）的值。其实原理也比较简单。

"""函数说明: 二分k-均值聚类算法
Parameters: dataSet - 给定的数据集 k - 簇的个数（要想分出几个簇，就需要有几个质心） distMeas - 计算距离的方法，默认使用欧氏距离Returns: mat(centList) - 质心列表 clusterAssment - 点分配结果。存储每个点的簇分配结果的矩阵，第一列记录簇索引值，第二列存储误差（当前点到簇质心的距离的平方值）""" def biKmeans(dataSet, k, distMeas=distEclud): m = shape(dataSet)[0] # 获得数据集的 行数，也就是 数据点 的个数 clusterAssment = mat(zeros((m,2))) # 创建一个 m*2 的矩阵,存储点分类结果。每一行的结果对应数据集的每一行  # 创建一个初始簇 centroid0 = mean(dataSet, axis=0).tolist()[0] # 沿矩阵的列方向（axis=0） 计算所有点的均值 centList =[centroid0] # 创建一个列表存储所有的质心  # 计算初始误差 for j in range(m): clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2 # 第二列存储误差（当前点到簇质心的距离的平方值）  while (len(centList) < k): lowestSSE = inf # 开始时将最小SSE设为无穷大  # 遍历所有的簇来决定最佳的簇进行分类 for i in range(len(centList)): ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:] # 将簇i中的所有点看做一个小的数据集 centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) # 对这个小数据集使用K-均值算法，将其分出两个簇。获得两个质心以及每个簇的误差 sseSplit = sum(splitClustAss[:,1]) sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) print("sseSplit, and notSplit: ",sseSplit,sseNotSplit) if (sseSplit + sseNotSplit) < lowestSSE: bestCentToSplit = i bestNewCents = centroidMat bestClustAss = splitClustAss.copy() lowestSSE = sseSplit + sseNotSplit  # 更新簇的分配结果 bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit print('the bestCentToSplit is: ',bestCentToSplit) print('the len of bestClustAss is: ', len(bestClustAss))  # 用两个最佳质心替换原来的一个质心 centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]  centList.append(bestNewCents[1,:].tolist()[0])  clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss #重新分配 新的簇 和 SSE  return mat(centList), clusterAssment

同样也可以按照k-均值算法里面的代码试一试二分K-均值算法，这里就不在赘述了。

5、对地图上的点进行聚类 

这个案例 比较简单，不多说，直接上代码。（其地址与经纬度的转换使用的是雅虎地址转换的API）

import urllibimport json
"""函数说明: 获得指定地点的经纬度
Parameters: stAddress - 街道地址 city - 城市Returns: 经纬度（字典类型）""" def geoGrab(stAddress, city): apiStem = 'http://where.yahooapis.com/geocode?' #create a dict and constants for the goecoder params = {} params['flags'] = 'J' #JSON return type params['appid'] = 'aaa0VN6k' params['location'] = '%s %s' % (stAddress, city) url_params = urllib.parse.urlencode(params) yahooApi = apiStem + url_params #print url_params print(yahooApi) c=urllib.request.urlopen(yahooApi) return json.loads(c.read())
from time import sleep
"""函数说明: 将获得的所有的地址信息存储到文件里
Parameters: fileName - 文件名Returns: 无""" def massPlaceFind(fileName): fw = open('places.txt', 'w') for line in open(fileName).readlines(): # 按行读取文件 line = line.strip() lineArr = line.split('	') retDict = geoGrab(lineArr[1], lineArr[2]) # 获得文件中 第二列 和 第三列 的内容，然后获取经纬度 if retDict['ResultSet']['Error'] == 0: lat = float(retDict['ResultSet']['Results'][0]['latitude']) lng = float(retDict['ResultSet']['Results'][0]['longitude']) print("%s	%f	%f" % (lineArr[0], lat, lng)) fw.write('%s	%f	%f
' % (line, lat, lng)) else: print("error fetching") sleep(1) # 睡眠一秒，确保不要再短时间内过于频繁的访问API，以免被封掉 fw.close() """函数说明: 球面距离计算
Parameters: vecA - 地点1的经纬度 vecB - 地点二的经纬度Returns: 地球上两点之间的距离，单位为：英里""" def distSLC(vecA, vecB): a = sin(vecA[0,1]*pi/180) * sin(vecB[0,1]*pi/180) #pi is imported with numpy b = cos(vecA[0,1]*pi/180) * cos(vecB[0,1]*pi/180) * cos(pi * (vecB[0,0]-vecA[0,0]) / 180) return arccos(a + b)*6371.0 
import matplotlibimport matplotlib.pyplot as plt
"""函数说明: 簇绘图函数
Parameters: numClust - 希望得到的簇数目Returns: 无""" def clusterClubs(numClust=5): datList = [] for line in open('places.txt').readlines(): lineArr = line.split('	') datList.append([float(lineArr[4]), float(lineArr[3])]) datMat = mat(datList)  myCentroids, clustAssing = biKmeans(datMat, numClust, distMeas=distSLC)  fig = plt.figure() # 创建画布 rect = [0.1,0.1,0.8,0.8] # 设置一个矩形 scatterMarkers=['s', 'o', '^', '8', 'p', 'd', 'v', 'h', '>', '<'] # 标记形状的列表  axprops = dict(xticks=[], yticks=[]) ax0 = fig.add_axes(rect, label='ax0', **axprops) # 画出矩形 imgP = plt.imread('Portland.png') # 基于一幅图来创建矩阵 ax0.imshow(imgP) # 绘制该矩阵  ax1 = fig.add_axes(rect, label='ax1', frameon=False) # 再画出一个同样的矩形 for i in range(numClust): ptsInCurrCluster = datMat[nonzero(clustAssing[:,0].A==i)[0],:] markerStyle = scatterMarkers[i % len(scatterMarkers)] # 使用索引来选择标记形状 ax1.scatter(ptsInCurrCluster[:,0].flatten().A[0], ptsInCurrCluster[:,1].flatten().A[0], marker=markerStyle, s=90)  ax1.scatter(myCentroids[:,0].flatten().A[0], myCentroids[:,1].flatten().A[0], marker='+', s=300) # 使用 十字标记 显示簇中心 plt.show()

直接运行 clusterClubs函数就可以看到效果了。

5、总结             

聚类与分类最大的不同是，分类的目标事先已知，而聚类则不一样，其类别没有预先定义。

K均值聚类容易实现，但其可能收敛到局部最小值，且在大规模数据上收敛得较慢。通常情况下，簇质心可以代表整个簇的数据来做出决策。

下篇文章会介绍使用sklearn实现K均值聚类，及其的评估指标--轮廓系数，以及对其k的调参。