BFS和DFS算法

Posted 2023-04-27

参考技术A

二分图 ：图中的点分为两组，且所有变都跨越组的边界，即为二分图。或言：把一个图的定点划分为两个不相交集；

匹配 ：在图论中，匹配是一个边的集合，任一两条边没有公共顶点；

最大匹配 ：一个图中所有匹配中，所含匹配边最多的匹配；

完美匹配 ：一个图中的匹配，所有顶点均为匹配点;

图 ：数学上，一个图是表示 物体与物体之间关系 的方法，是图论基本研究对象。一个图看起来就是由一些小圆点和连接这些远点的直线或曲线组成。

Breadth-First-Search，宽度优先搜索；

BFS 的步骤：

Depth-first search，深度优先搜索;

DFS 的步骤：（不到尽头不回头）

直接开一个 N×N 的二维数组 E，然后 E [i][j] 为 1 的时候表示 i 和 j 之间有一条边，0 的时候就没有。

缺点 ：

使用 链表的方式（vector） 保存一个结点的所有边;

和链表几乎没什么区别，就是每次添加新的边的时候往开头加，而不是往最后加。（不太理解，暂不扩展）

1. 二分图的最大匹配、完美匹配和匈牙利算法

2. BFS 和 DFS 算法原理（通俗易懂版）

3. BFS 、DFS 区别，详解

熬夜怒肝，图解算法！BFS和DFS的直观解释

一、前言

我们首次接触 BFS 和 DFS 时，应该是在数据结构课上讲的 “图的遍历”。还有就是刷题的时候，遍历二叉树我们会经常用到BFS和DFS。它们的实现都很简单，这里我就不哆嗦去贴代码了。

想看代码的可以看《剑指Offer（三十八）：二叉树的深度》这个题目就可以利用BFS和DFS进行求解。那么，这两者“遍历” 的序列到底有何差别？

本篇文章就单纯来讲讲它们的区别和各自的应用，不会涉及任何代码。我们以“图的遍历”为例，进行说明。

二、区别

广度优先搜索算法（Breadth-First-Search，缩写为 BFS），是一种利用队列实现的搜索算法。简单来说，其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。

深度优先搜索算法（Depth-First-Search，缩写为 DFS），是一种利用递归实现的搜索算法。简单来说，其搜索过程和 “不撞南墙不回头” 类似。

BFS 的重点在于队列，而 DFS 的重点在于递归。这是它们的本质区别。

举个典型例子，如下图，灰色代表墙壁，绿色代表起点，红色代表终点，规定每次只能走一步，且只能往下或右走。求一条绿色到红色的最短路径。

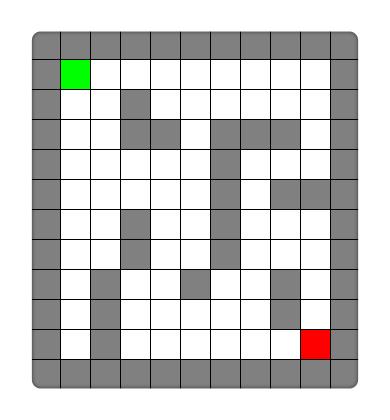
对于上面的问题，BFS 和 DFS 都可以求出结果，它们的区别就是在复杂度上存在差异。我可以先告诉你，该题 BFS 是较佳算法。

BFS示意图：

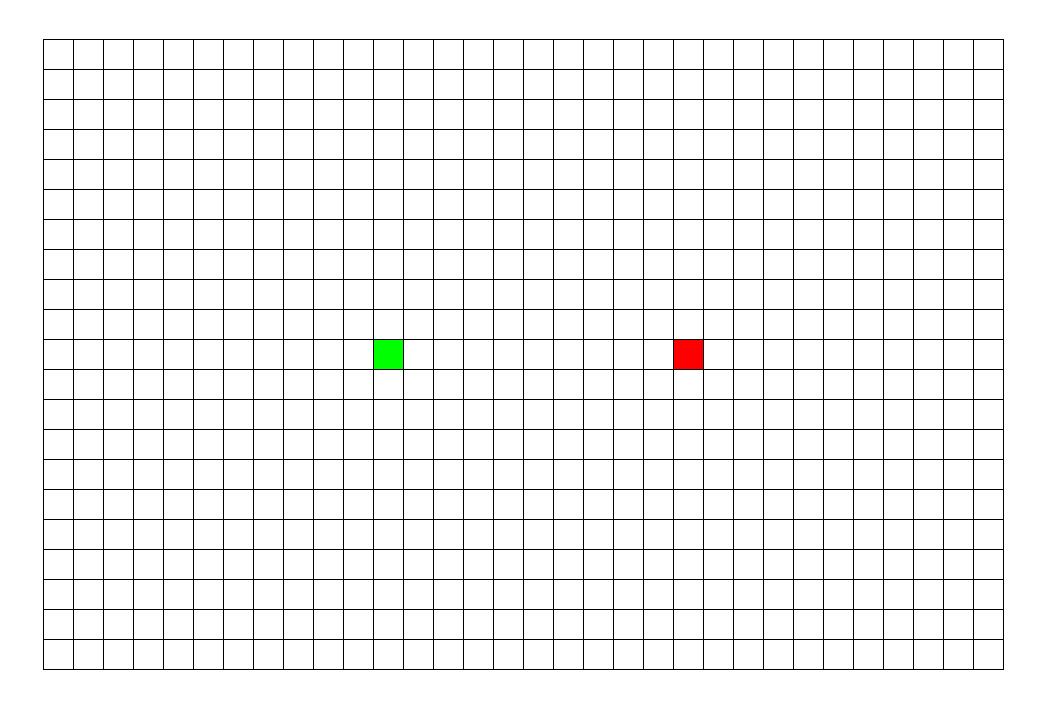
如上图所示，从起点出发，对于每次出队列的点，都要遍历其四周的点。所以说 BFS 的搜索过程和 “湖面丢进一块石头激起层层涟漪” 很相似，此即 “广度优先搜索算法” 中“广度”的由来。

DFS示意图：

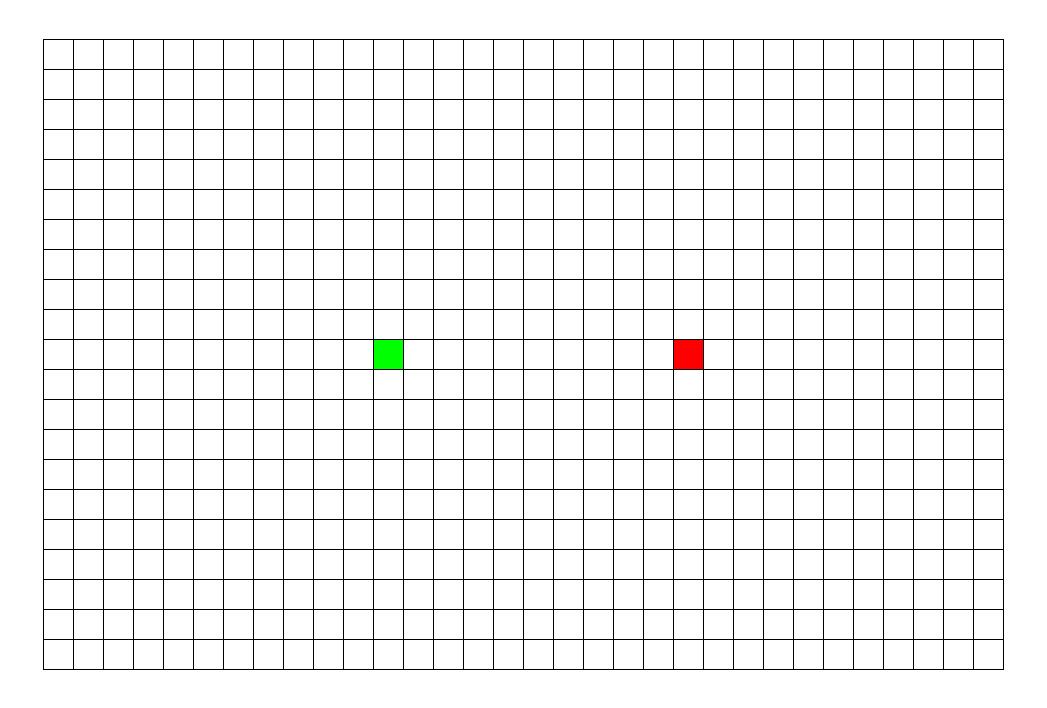
三、总结

现在，你不妨对照着图，再去看看你打印出的遍历序列，是不是一目了然呢？

最后再说下它们的应用方向。

BFS 常用于找单一的最短路线，它的特点是 "搜到就是最优解"，而 DFS 用于找所有解的问题，它的空间效率高，而且找到的不一定是最优解，必须记录并完成整个搜索，故一般情况下，深搜需要非常高效的剪枝（剪枝的概念请百度）。

PS：BFS 和 DFS 是很重要的算法，读者如果想要更深入地了解它们，建议去 OJ 或 Leetcode 上找一些相关赛题训练下，一定会给你一个别样的天地。

如上图所示，从起点出发，先把一个方向的点都遍历完才会改变方向...... 所以说，DFS 的搜索过程和 “不撞南墙不回头” 很相似，此即 “深度优先搜索算法” 中“深度”的由来。

最后再送大家一本，帮助我拿到 BAT 等一线大厂 offer 的数据结构刷题笔记，是一位 Google 大神写的，对于算法薄弱或者需要提高的同学都十分受用：

谷歌和阿里大佬的Leetcode刷题笔记

以及我整理的 BAT 算法工程师学习路线，书籍+视频，完整的学习路线和说明，对于想成为算法工程师的，绝对能有所帮助（提取码：jack）：

我是如何成为算法工程师的，超详细的学习路线

别光收藏，来个赞哦，笔芯~