6根孔明锁的B系列的解法？（带图）

Posted 2023-04-26

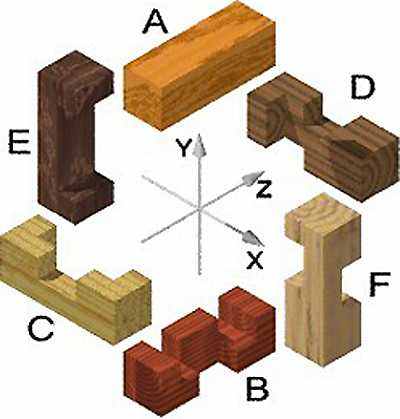
参考技术A

6根孔明锁观察其基本结构，如下图。

常见的六根孔明锁由上图中这六根木条的组装而成，上图第一行是朝上摆放的各块件，第二行是朝下摆放的各块件。第一根是完全实心的木条，新手建议模仿本文中的各部件摆放位置以便接下来好跟着图解步骤完成还原。六根孔明锁的各块件编号如下所示：

6根孔明锁的解法共有两种，第一种解法如下图：

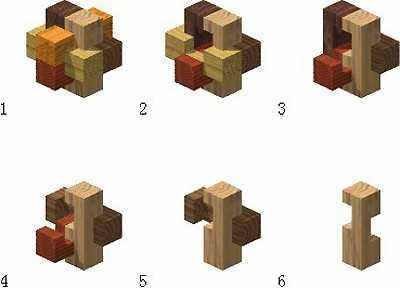
上图是第一种拆解孔明锁的方法——按照先后顺序，从块件A开始，然后依次拆解块件C 、E、 B、 D，最后只剩下块件F，这样就可以拆解孔明锁了。

第二种解法如下图。

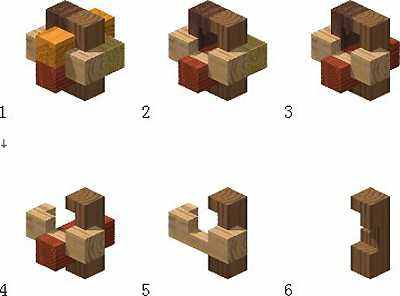
解法2的拆解顺序实际上与解法1相同，从块件A开始，然后依次拆解块件C 、E、 B、 D，最后只剩下块件F。细心观察不难发现，解法一和解法二中的孔明锁初始的装配顺序不一样，所以要把它们分为两种不同解法。

10-看图理解数据结构与算法系列(B+树)

B+树

B+树是B树的一种变体，也属于平衡多路查找树，大体结构与B树相同，包含根节点、内部节点和叶子节点。多用于数据库和操作系统的文件系统中，由于B+树内部节点不保存数据，所以能在内存中存放更多索引，增加缓存命中率。另外因为叶子节点相连遍历操作很方便，而且数据也具有顺序性，便于区间查找。

B+树特点

• B+树可以定义一个m值作为预定范围，即m路(阶)B+树。
• 根节点可能是叶子节点，也可能是包含两个或两个以上子节点的节点。
• 内部节点如果拥有k个关键字则有k+1个子节点。
• 非叶子节点不保存数据，只保存关键字用作索引，所有数据都保存在叶子节点中。
• 非叶子节点有若干子树指针，如果非叶子节点关键字为k1,k2,...kn，其中n=m-1，那么第一个子树关键字判断条件为小于k1，第二个为大于等于k1而小于k2，以此类推，最后一个为大于等于kn，总共可以划分出m个区间，即可以有m个分支。（判断条件其实没有严格的要求，只要能实现对B+树的数据进行定位划分即可，有些实现使用了m个关键字来划分区间，也是可以的）
• 所有叶子节点通过指针链相连，且叶子节点本身按关键字的大小从小到大顺序排列。
• 自然插入而不进行删除操作时，叶子节点项的个数范围为[floor(m/2),m-1]，内部节点项的个数范围为[ceil(m/2)-1,m-1]。
• 另外通常B+树有两个头指针，一个指向根节点一个指向关键字最小的叶子节点。
• 在进行删除操作时，涉及到索引节点填充因子和叶子节点填充因子，一般可设叶子节点和索引节点的填充因子都不少于50%。

以下是一棵4阶B+树，

 

 

插入操作

假设现在构建一棵四阶B+树，开始插入“A”，直接作为根节点，

 

 

插入“B”，大于“A”，放右边，

 

 

插入“C”，按顺序排到最后，

 

 

继续插入“D”，直接添加的结果如下图，此时超过了节点可以存放容量，对于四阶B+树每个节点最多存放3个项，此时需要执行分裂操作，

 

 

分裂操作为，先选取待分裂节点中间位置的项，这里选“C”，然后将“C”项放到父节点中，因为这里还没有父节点，那么直接创建一个新的父节点存放“C”，而原来小于“C”的那些项作为左子树，原来大于等于“C”的那些项作为右子树。这里注意下非叶子节点存放的都是关键字，用作索引的，所以父节点存放的“C”项不包括数据，数据仍然存放在右子树。此外，还需要添加一个指针，由左子树指向右子树。

 

 

继续插入“M”，“M”大于“C”，往右子节点，

 

 

分别与“C”“D”比较，大于它们，放到最右边，

 

 

插入“L”，“L”大于“B”，往右子树，

 

 

“L”逐一与节点内项的值比较，根据大小放到指定位置，此时触发分裂操作，

 

 

选取待分裂节点中间位置的项“L”，然后将“L”项放到父节点中，按大小顺序将“L”放到指定位置，而原来小于“L”的那些项作为左子树，原来大于等于“L”的那些项作为右子树。父节点存放的“L”项不包括数据，数据仍然存放在右子树。此外，还需要在左子树中添加一个指向右子树的指针。

 

 

继续插入“K”，从根节点开始查找，逐一比较关键字，“K”大于“C”而小于“L”，往第二个分支，

 

 

在子节点中逐一比较，“K”最终落在最右边，

 

 

继续插入“J”，从根节点开始查找，逐一比较关键字，“J”大于“C”而小于“L”，往第二个分支，

 

 

在子节点中找到“J”的相应位置，此时超过了节点的容量，需要进行分裂操作，

 

 

选取待分裂节点中间位置的项“J”，然后将“J”项放到父节点中，按大小顺序将“J”放到指定位置，而原来小于“J”的那些项作为左子树，原来大于等于“J”的那些项作为右子树。父节点存放的“J”项不包括数据，数据仍然存放在右子树。此外，还需要在左子树中添加一个指向右子树的指针。

 

 

继续插入“I”，从根节点开始查找，逐一比较关键字，“I”大于“C”而小于“J”“L”，往第二个分支，

 

 

逐一比较找到“I”的插入位置，

 

 

继续插入“H”，从根节点开始查找，逐一比较关键字，“H”大于“C”而小于“J”“L”，往第二个分支，

 

 

“H”逐一与节点内的值比较，根据大小放到指定位置，此时触发分裂操作，

 

 

选取待分裂节点中间位置的项“H”，然后将“H”项放到父节点中，按大小顺序将“H”放到指定位置，而原来小于“H”的那些项作为左子树，原来大于等于“H”的那些项作为右子树。父节点存放的“H”项不包括数据，数据仍然存放在右子树。此外，还需要在左子树中添加一个指向右子树的指针。

但此时父节点超出了容量，父节点需要继续分裂操作，

 

 

选取待分裂节点中间位置的项“J”，然后将“J”项放到父节点中，但还不存在父节点，需要创建一个作为父节点。原来小于“J”的那些项作为左子树，原来大于“J”的那些项作为右子树。这是非叶子节点的分裂，操作对象都是用作索引的关键字，不必考虑数据存放问题。

 

 

插入“G”，从根节点开始查找，“G”小于“J”，往第一个分支，

 

 

逐一比较节点内项的值，“G”大于“C”小于“H”，往第二个分支，

 

 

逐一比较节点内项的值，找到“G”的位置并插入，

 

 

插入“F”，从根节点开始查找，“F”小于“J”，往第一个分支，

 

 

逐一比较节点内项的值，“F”大于“C”小于“H”，往第二个分支，

 

 

逐一比较节点内项的值，找到“F”的位置并插入，此时触发分裂操作，

 

 

选取待分裂节点中间位置的项“F”，然后将“F”项放到父节点中，按大小顺序将“F”放到指定位置，而原来小于“F”的那些项作为左子树，原来大于等于“F”的那些项作为右子树。父节点存放的“F”项不包括数据，数据仍然存放在右子树。此外，还需要在左子树中添加一个指向右子树的指针。

 

 

最后插入“E”，从根节点开始查找，“E”小于“J”，往第一个分支，

 

 

逐一比较节点内项的值，“E”大于“C”小于“F”，往第二个分支，

 

 

逐一比较节点内项的值，找打“E”适当的位置并插入。

 

 

从上面插入操作可以总结，插入主要就是涉及到分裂操作，而且要注意到非节点只保存了关键字作为索引，而数据都保存在叶子节点上，此外还需要使用指针将叶子节点连接起来。最终我们可以看到叶子节点的项按从小到大排列，因为有了指针使得可以很方便遍历数据。

查找操作

对B+树的查找与B树的查找差不多，从根节点开始查找，通过比较项的值找到对应的分支，然后继续往子树上查找。

比如查找“H”，“H”小于“J”，往第一个分支，

 

 

逐一比较节点中的项，发现应该往第四个分支，

 

 

逐一比较，找到“H”。

 

 

遍历操作

遍历操作首先是要先找到树最左边的叶子节点，然后就可以通过指针完成整棵树的遍历了。

从根节点开始，一直往第一个分支走，

 

 

继续往第一个分支走，

 

 

发现已经到叶子节点了，这就是要找的遍历的开端，

 

 

第一个叶子节点有两个项，接着根据指针跳到第二个叶子节点，

 

 

第二个节点有三个项，根据指针继续往下一个节点，

 

 

该节点有两个项，根据指针继续往下一个节点，

 

 

不断根据指针往下，

 

 

往下，

 

 

完成整棵树的遍历。

 

作者：超人汪小建
链接：https://juejin.im/post/5b9073f9f265da0acd209624
来源：掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。