魔方阵的C语言

Posted 2023-04-26

代码一：
#include <stdio.h>
#define N 16 //这里可以修改N的值，并且N只能为偶数
int main()

int a[N][N]=0,i,j,k,p,m,n;
p=1;
while(p==1)

printf(Enter n（1~%d): ,N-1);/*可以输入小于等于N-1的奇数*/
scanf(%d,&n);
if((n!=0)&&(n<N)&&(n%2!=0)) p=0;

i=n+1;
j=n/2+1; /*建立魔方阵*/
a[1][j]=1;
for(k=2;k<=n*n;k++)

i=i-1;
j=j+1;
if((i<1)&&(j>n))

i=i+2;j=j-1;

else

if(i<1) i=n;
if(j>n) j=1;

if(a[i][j]==0) a[i][j]=k;
else

i=i+2;
j=j-1;
a[i][j]=k;


for(i=1;i<=n;i++)/*输出魔方阵*/

for(j=1;j<=n;j++)
printf(%4d,a[i][j]);
printf(\\n);


代码二：（相对于代码一条理更清晰，更简单、更容易理解）
将1～n的平方这几个数构成一个n阶魔方阵。
算法：
依以下法则，你可以很快的写出奇数阶幻方！当然，这种写法只是其中一个答案，而不是唯一答案。
1）将1填入第一行中间；
2）将每个数填在前一个数的右上方。
3）若该位置超出最上行，则改填在最下行的对应位置；
4）若该位置超出最右列，则该填在最左列的对应行位置；
5）若某元素填在第一行最右列，下一个数填在该数同列的下一行；
6）若某数已填好，但其右上角已填了其他数据，则下一个数填在该数同列的下一行位置。
#include<stdio.h>
void main()

int a[15][15]=0,i,j,m,n,temp,M;
printf(请输入一个3~15的奇数：\\n);
scanf(%d,&M);
i=0;
j=M/2;
a[i][j]=1;
for(temp=2;temp<=M*M;temp++)

m=i;
n=j;
i--;
j++;
if(i<0)
i=M-1;
if(j>M-1）
j=0;
if(a[i][j]!=0)

i=m+1,j=n;
a[i][j]=temp;
continue;

a[i][j]=temp;

printf(%d×%d魔方阵：\\n,M,M);
for(i=0;i<M;i++)

for(j=0;j<M;j++)
printf(%4d,a[i][j]);
printf(\\n);


//（求4的倍数阶幻方）
void main()

int i,j,x,y,n,t,k=1;
int a[100][100];
printf(请输入魔方阵的阶数n \\n);
scanf(%d,&n);
printf(输出为：\\n);
if(n%4==0)

for(i=0;i<n;i++)
for(j=0;j<n;j++)

a[i][j]=k;
k++;

x=n-1;
for(j=0;j<n/2;j++,x--)

for(i=0;i<n;i++)
if(i%4!=j%4&&(i+j)%4!=3）

t=a[i][j];
a[i][j]=a[i][x];
a[i][x]=t;


x=n-1;
for(i=0;i<n/2;i++,x--)

for(j=0;j<n;j++)
if(i%4!=j%4&&(i+j)%4!=3）

t=a[i][j];
a[i][j]=a[x][j];
a[x][j]=t;


for(i=0;i<n;i++)

for(j=0;j<n;j++)
printf(%-4d,a[i][j]);
printf(\\n);


else printf(输入错误\\n);
system(pause...);

参考技术A

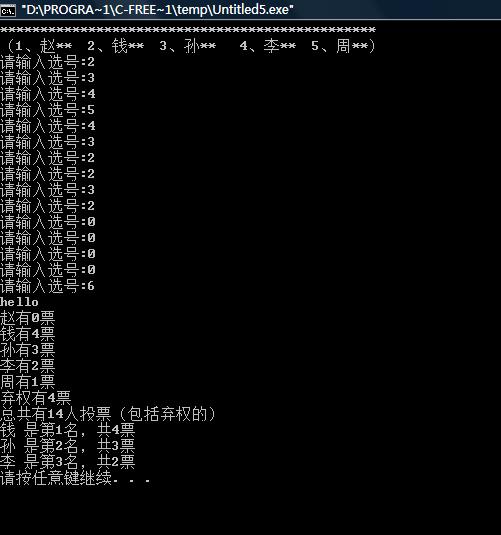
效果图：

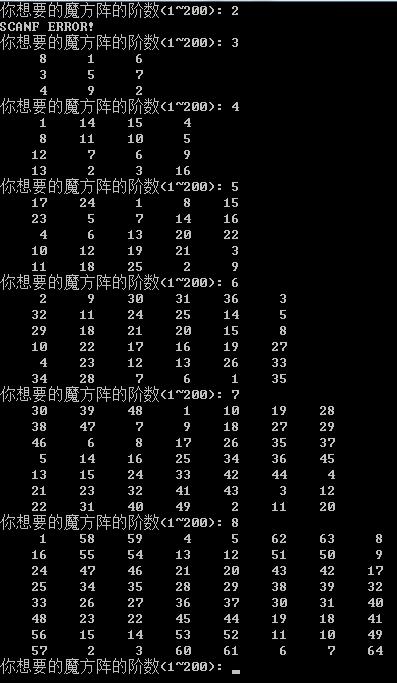
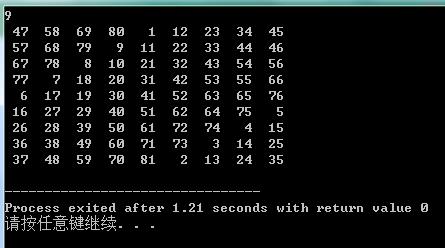
代码如下：

/*该程序由本人[百度帐号：prende]查阅多项资料后亲自编写，转载请注明出处，谢谢！*/
#include<stdio.h>
int a[200][200]=0;           /*200为我自己定义的，可根据需要修改*/
void JSZ(int n)                                /*奇数魔方阵算法*/
int p,k,i,j;
 p=0;k=n/2;
 a[p][k]=1;
 for(i=2;i<=n*n;i++)
  if((i-1)%n==0)
    if(p==n-1)p=0;
     else p++;
    
   else
    if(p==0)p=n-1;
     else p--;
     if(k==n-1)k=0;
     else k++;
    
   a[p][k]=i;
  

void Ou4bZ(int n)                  /*偶数4的倍数魔方阵算法*/
int a1[200][200],a2[200][200],i,j;
 for(i=0;i<n;i++)
  for(j=0;j<n;j++)
   if(i%4==0||(i+1)%4==0)a1[i][j]=j+1;
    else a1[i][j]=n-j;
   
 for(j=0;j<n;j++)
  for(i=0;i<n;i++)
   if(j%4==0||(j+1)%4==0)a2[i][j]=n*i;
    else a2[i][j]=(n-1-i)*n;
   
 for(i=0;i<n;i++)
  for(j=0;j<n;j++)
   a[i][j]=a1[i][j]+a2[i][j];

void N_4OuZ(int n)                   /*偶数非4的倍数魔方阵算法*/
int s[200],x[200],z[200],y[200],i,p,k,b[200][200]=0;
 z[0]=4;z[1]=10;s[0]=2;s[1]=9;
 for(i=2;i<n/2-1;i++)
  if(i%2==0)
    z[i]=z[i-1]+1;
     s[i]=s[i-1]+3;
    
   else
    z[i]=z[i-1]+7;
     s[i]=s[i-1]+5;
    
  
 y[0]=3;y[1]=5;x[0]=1;x[1]=6;
 for(i=2;i<n/2;i++)
  if(i%2==0)
    y[i]=y[i-1]+3;
     x[i]=x[i-1]+1;
    
   else
    y[i]=y[i-1]+5;
     x[i]=x[i-1]+7;
    
  
 Ou4bZ(n-2);
 for(p=1;p<n-1;p++)
  for(k=1;k<n-1;k++)
   b[p][k]=a[p-1][k-1]+(n*n-(n-2)*(n-2))/2;
 for(p=1;p<n-1;p++)
  for(k=1;k<n-1;k++)
   a[p][k]=b[p][k];
 for(i=0;i<n/2-1;i++)
  a[0][i]=s[i];
   a[n-2-i][0]=z[i];
  
 for(i=0;i<n/2;i++)
  a[n-1][n-2-i]=x[i];
   a[i][n-1]=y[i];
  
 for(i=0;i<n;i++)
  if(i==0)a[n-1][0]=n*n+1-a[0][n-1];
   else if(i<n/2-1)a[n-1][i]=n*n+1-a[0][i];
   else if(i==n-1)a[n-1][n-1]=n*n+1-a[0][0];
   else a[0][i]=n*n+1-a[n-1][i];
   if(i>0&&i<n/2)a[i][0]=n*n+1-a[i][n-1];
   if(i>=n/2&&i<n-1)a[i][n-1]=n*n+1-a[i][0];
  

void main()/*主函数*/
int i,j,n;
 lp:printf("你想要的魔方阵的阶数(1~200): ");
 scanf("%d",&n);
 if(n<1||n==2||n>200)      /*由于没有二阶魔方阵，"n>200"为超出定义范围*/
  printf("SCANF ERROR!\\n");
   goto lp;
  
 if(n%2==0)
  if(n%4==0)Ou4bZ(n);
   else N_4OuZ(n);
  
 else JSZ(n);
 for(i=0;i<n;i++)
  for(j=0;j<n;j++)
    printf("%6d",a[i][j]);
   printf("\\n");
  
 goto lp;

参考技术B

奇数阶的魔方阵：

#include <stdio.h>
int main()
int a[19][19]=0,i,j,i1,j1,k,n;
 scanf("%d",&n);
 if(n>19||n%2==0)return 0;
 i=0;j=n/2;k=1;
 for(i1=0;i1<n;i1++)
 for(j1=0;j1<n-1;j1++)
    a[i][j]=k++;
     i=(i==0?n-1:--i);
     j=(j==n-1?0:++j);

a[i][j]=k++;
i++;
 
 for(i=0;i<n;i++)
 for(j=0;j<n;j++)
    printf("%3d ",a[i][j]);
  printf("\\n");  
    
 return 0;

2(2N+1) 魔方阵

由于作者不习惯该编辑器，只是贴出上本文的截图，详情见：
https://www.yuque.com/docs/share/d7aaf84a-bd72-43c6-bc48-d4e0e7a3b0cd