完全二叉树与满二叉树的区别是啥?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了完全二叉树与满二叉树的区别是啥?相关的知识,希望对你有一定的参考价值。
1、含义不同:
完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
2、表示不同:
对于满二叉树,除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。而完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
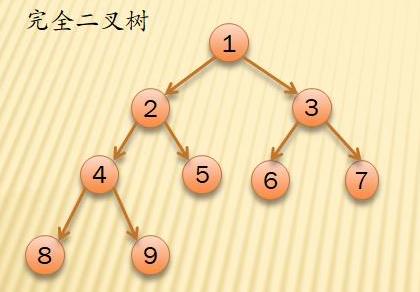
判断一棵树是否是完全二叉树的思路
1>如果树为空,则直接返回错
2>如果树不为空:层序遍历二叉树
2.1>如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列;
2.1>如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
2.2>如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空,且则该节点之后的队列中的结点都为叶子节点,该树才是完全二叉树,否则就不是完全二叉树;
以上内容参考:百度百科-完全二叉树
参考技术A完全二叉树与满二叉树的区别为:性质不同、包含不同、叶子结点不同。
一、性质不同
1、完全二叉树:深度为k,有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时,称为完全二叉树。
2、满二叉树:如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
二、包含不同
1、完全二叉树:完全二叉树包含满二叉树。
2、满二叉树:满二叉树是完全二叉树的特殊形态, 即如果一棵二叉树是满二叉树, 则它必定是完全二叉树。
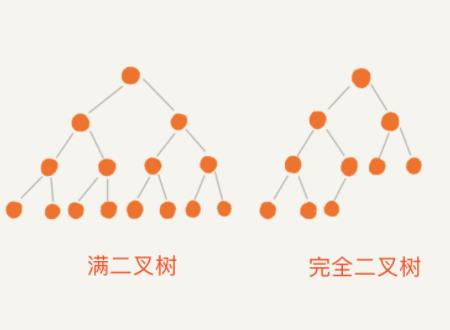
三、叶子结点不同
1、完全二叉树:完全二叉树的叶子结点可出现在最下层或次下层。
2、满二叉树:满二叉树的叶子结点只能出现在最下层和次下层。
参考技术B 1、含义不同:完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
2、表示不同:
对于满二叉树,除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。而完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。
对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
判断一棵树是否是完全二叉树的思路
1>如果树为空,则直接返回错
2>如果树不为空:层序遍历二叉树
2.1>如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列;
2.1>如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
二叉树--二叉树的宽度
来源:LeetCode
难度:中等
描述:
给定一个二叉树,编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树(full binary tree)结构相同,但一些节点为空。
每一层的宽度被定义为两个端点(该层最左和最右的非空节点,两端点间的null节点也计入长度)之间的长度。
示例1:
示例2:
分析:
注意本题中的宽度并不是每层的节点个数,而是基于整棵树是满二叉树的情况下,每层的宽度则为两个端点加上中间满二叉树缺失的节点的总个数
因此咱们只要计算出每个节点在满二叉树的情况下,在本层的所属的位置,那么本层的宽度就是两个端点的位置差。在满二叉树中,假设根节点的位置为position,那么左子节点的位置为position * 2,右子节点的位置为position * 2 + 1,通过上面的公式很容易就能得到每个节点所属位置。具体解法如下
解题
方法一:深度优先遍历
思路:
首先咱们需要记录每个节点的位置,假设根节点的位置为position,左节点为position * 2,右节点则为position * 2 + 1
其次采用深度遍历的方式遍历二叉树,每层第一个被遍历的节点就是该层的最左边的节点,因此采用map将每层的深度和其最左节点记录下来,所以每层的宽度则是该深度下最右边的位置减去 最左边的位置 加 1
记录每层的宽度,并保留最大值即可
代码:
1private int ans;
2public int widthOfBinaryTree(TreeNode root) {
3 Map<Integer, Integer> dept2LeftPosition = new HashMap<>();
4 dfs(root, 0, 0, dept2LeftPosition);
5 return ans;
6}
7public void dfs(TreeNode root, int depth, int pos,
8 Map<Integer, Integer> dept2LeftPosition) {
9 if (root == null) {
10 return;
11 }
12 if (!dept2LeftPosition.containsKey(depth)) {
13 //记录每层的最左边位置
14 dept2LeftPosition.put(depth, pos);
15 }
16 //ans = max(每个节点位置 - 本层中最左节点位置 + 1, ans)
17 ans = Math.max(ans, pos - dept2LeftPosition.get(depth) + 1);
18 //递归左右子树
19 dfs(root.left, depth + 1, 2 * pos, dept2LeftPosition);
20 dfs(root.right, depth + 1, 2 * pos + 1, dept2LeftPosition);
21}
时间复杂度:O(n) n是节点个数
空间复杂度:O(n)
方法二:广度优先遍历
思路:
每个节点位置的计算公式和上面一样,只是这里采用队列存储每一层的节点,同理采用一个链表记录每个节点对应的位置。
当队列的节点出队时,其对应的位置也从链表中移除,这样保证了链表中的位置是严格按照节点进入队列的位置来排列的,即链表头是每层中最左节点位置,链表尾是每层中最右节点位置。
因此每层宽度等于链表尾的值 - 链表头的值 + 1
代码:
1public int widthOfBinaryTree(TreeNode root) {
2 if (root == null) {
3 return 0;
4 }
5 //利用队列存储每层节点
6 Queue<TreeNode> queue = new LinkedList<>();
7 //利用List链表存储每层中每个节点的位置
8 LinkedList<Integer> list = new LinkedList<>();
9 queue.offer(root);
10 list.add(1);
11 int res = 1;
12 while (!queue.isEmpty()) {
13 int size = queue.size();
14 for (int i = 0; i < size; i++) {
15 //节点出队
16 TreeNode cur = queue.poll();
17 //节点出队的同时将其对应的位置移除链表,
18 //当本层节点全部出队时,其所有对应的节点也将全部移除链表
19 Integer curIndex = list.removeFirst();
20 if (cur.left != null) {
21 queue.offer(cur.left);
22 //存储每个节点位置
23 list.add(curIndex * 2);
24 }
25 if (cur.right != null) {
26 queue.offer(cur.right);
27 list.add(curIndex * 2 + 1);
28 }
29 }
30 // list 中 size 为 1 的情况下,宽度也为 1,没有必要计算。
31 if (list.size() >= 2) {
32 //每层的宽度 = 最右边的位置 - 最左边的位置 + 1
33 res = Math.max(res, list.getLast() - list.getFirst() + 1);
34 }
35 }
36 return res;
37}
时间复杂度:O(n) n是节点个数
空间复杂度:O(n)
往期精彩推荐
以上是关于完全二叉树与满二叉树的区别是啥?的主要内容,如果未能解决你的问题,请参考以下文章