Akima 插值和样条插值的C语言源代码,要有注释。
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Akima 插值和样条插值的C语言源代码,要有注释。相关的知识,希望对你有一定的参考价值。
参考技术AAkima 插值
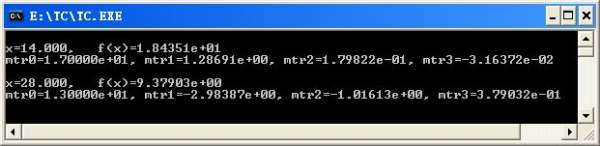
附带的图片为运行结果
#include "stdio.h"
#include "math.h"
#include "interpolation.h"
void interpolation_akima(AKINTEP ap)
int num,k,kk,m,l;
double pio,*mtr,*x,*y,u[5],p,q;
num=ap->n; k=ap->k;
pio=ap->t; mtr=ap->s;
x=ap->x; y=ap->y;
if (num<1)
return;
else if (num==1)
mtr[0]=mtr[4]=y[0];
return;
else if (num==2)
mtr[0]=y[0];
mtr[1]=(y[1]-y[0])/(x[1]-x[0]);
if (k<0)
mtr[4]=(y[0]*(pio-x[1])-y[1]*(pio-x[0]))/(x[0]-x[1]);
return;
if (k<0)
if (pio<=x[1]) kk=0;
else if (pio>=x[num-1]) kk=num-2;
else
kk=1; m=num;
while (((kk-m)!=1)&&((kk-m)!=-1))
l=(kk+m)/2;
if (pio<x[l-1]) m=l;
else kk=l;
kk--;
else kk=k;
if (kk>=num-1) kk=num-2;
u[2]=(y[kk+1]-y[kk])/(x[kk+1]-x[kk]);
if (num==3)
if (kk==0)
u[3]=(y[2]-y[1])/(x[2]-x[1]);
u[4]=2.0*u[3]-u[2];
u[1]=2.0*u[2]-u[3];
u[0]=2.0*u[1]-u[2];
else
u[1]=(y[1]-y[0])/(x[1]-x[0]);
u[0]=2.0*u[1]-u[2];
u[3]=2.0*u[2]-u[1];
u[4]=2.0*u[3]-u[2];
else
if (kk<=1)
u[3]=(y[kk+2]-y[kk+1])/(x[kk+2]-x[kk+1]);
if (kk==1)
u[1]=(y[1]-y[0])/(x[1]-x[0]);
u[0]=2.0*u[1]-u[2];
if (num==4) u[4]=2.0*u[3]-u[2];
else u[4]=(y[4]-y[3])/(x[4]-x[3]);
else
u[1]=2.0*u[2]-u[3];
u[0]=2.0*u[1]-u[2];
u[4]=(y[3]-y[2])/(x[3]-x[2]);
else if (kk>=(num-3))
u[1]=(y[kk]-y[kk-1])/(x[kk]-x[kk-1]);
if (kk==(num-3))
u[3]=(y[num-1]-y[num-2])/(x[num-1]-x[num-2]);
u[4]=2.0*u[3]-u[2];
if (num==4) u[0]=2.0*u[1]-u[2];
else u[0]=(y[kk-1]-y[kk-2])/(x[kk-1]-x[kk-2]);
else
u[3]=2.0*u[2]-u[1];
u[4]=2.0*u[3]-u[2];
u[0]=(y[kk-1]-y[kk-2])/(x[kk-1]-x[kk-2]);
else
u[1]=(y[kk]-y[kk-1])/(x[kk]-x[kk-1]);
u[0]=(y[kk-1]-y[kk-2])/(x[kk-1]-x[kk-2]);
u[3]=(y[kk+2]-y[kk+1])/(x[kk+2]-x[kk+1]);
u[4]=(y[kk+3]-y[kk+2])/(x[kk+3]-x[kk+2]);
mtr[0]=fabs(u[3]-u[2]);
mtr[1]=fabs(u[0]-u[1]);
if ((fabs(mtr[0])<0.0000001)&&(fabs(mtr[1])<0.0000001))
p=(u[1]+u[2])/2.0;
else p=(mtr[0]*u[1]+mtr[1]*u[2])/(mtr[0]+mtr[1]);
mtr[0]=fabs(u[3]-u[4]);
mtr[1]=fabs(u[2]-u[1]);
if ((fabs(mtr[0])<0.0000001)&&(fabs(mtr[1])<0.0000001))
q=(u[2]+u[3])/2.0;
else q=(mtr[0]*u[2]+mtr[1]*u[3])/(mtr[0]+mtr[1]);
mtr[0]=y[kk];
mtr[1]=p;
mtr[3]=x[kk+1]-x[kk];
mtr[2]=(3.0*u[2]-2.0*p-q)/mtr[3];
mtr[3]=(q+p-2.0*u[2])/(mtr[3]*mtr[3]);
if (k<0)
p=pio-x[kk];
mtr[4]=mtr[0]+mtr[1]*p+mtr[2]*p*p+mtr[3]*p*p*p;
return;
main()
double x[11]=3.0,5.0,8.0,13.0,17.0,25.0,27.0,29.0,31.0,35.0,39.0;
double y[11]=7.0,10.0,11.0,17.0,23.0,18.0,13.0,6.0,3.0,1.0,0.0;
AKINTE aa= 11, x, y, -1, 14.0, 0;
AKINTE ab= 11, x, y, -1, 28.0, 0;
printf("\\n");
interpolation_akima(&aa);
printf("x=%6.3f, f(x)=%e\\n",aa.t, aa.s[4]);
printf("mtr0=%e, mtr1=%e, mtr2=%e, mtr3=%e\\n",aa.s[0],aa.s[1],aa.s[2],aa.s[3]);
printf("\\n");
interpolation_akima(&ab);
printf("x=%6.3f, f(x)=%e\\n",ab.t, ab.s[4]);
printf("mtr0=%e, mtr1=%e, mtr2=%e, mtr3=%e\\n",ab.s[0],ab.s[1],ab.s[2],ab.s[3]);
printf("\\n");
三次样条插值的实现
1、程序比较简单的:
#include<iostream>
#include<iomanip>
using namespace std;
const int MAX = 50;
float x[MAX], y[MAX], h[MAX];
float c[MAX], a[MAX], fxym[MAX];
float f(int x1, int x2, int x3)
float a = (y[x3] - y[x2]) / (x[x3] - x[x2]);
float b = (y[x2] - y[x1]) / (x[x2] - x[x1]);
return (a - b)/(x[x3] - x[x1]);
//求差分
void cal_m(int n) //用追赶法求解出弯矩向量M……
float B[MAX];
B[0] = c[0] / 2;
for(int i = 1; i < n; i++)
B[i] = c[i] / (2 - a[i]*B[i-1]);
fxym[0] = fxym[0] / 2;
for(i = 1; i <= n; i++)
fxym[i] = (fxym[i] - a[i]*fxym[i-1]) / (2 - a[i]*B[i-1]);
for(i = n-1; i >= 0; i--)
fxym[i] = fxym[i] - B[i]*fxym[i+1];
void printout(int n);
int main()
int n,i; char ch;
do
cout<<"Please put in the number of the dots:";
cin>>n;
for(i = 0; i <= n; i++)
cout<<"Please put in X"<<i<<':';
cin>>x[i]; //cout<<endl;
cout<<"Please put in Y"<<i<<':';
cin>>y[i]; //cout<<endl;
for(i = 0; i < n; i++) //求 步长
h[i] = x[i+1] - x[i];
cout<<"Please 输入边界条件\\n 1: 已知两端的一阶导数\\n 2:两端的二阶导数已知\\n 默认:自然边界条件\\n";
int t;
float f0, f1;
cin>>t;
switch(t)
case 1:cout<<"Please put in Y0\\' Y"<<n<<"\\'\\n";
cin>>f0>>f1;
c[0] = 1; a[n] = 1;
fxym[0] = 6*((y[1] - y[0]) / (x[1] - x[0]) - f0) / h[0];
fxym[n] = 6*(f1 - (y[n] - y[n-1]) / (x[n] - x[n-1])) / h[n-1];
break;
case 2:cout<<"Please put in Y0\\" Y"<<n<<"\\"\\n";
cin>>f0>>f1;
c[0] = a[n] = 0;
fxym[0] = 2*f0; fxym[n] = 2*f1;
break;
default:cout<<"不可用\\n";//待定
;//switch
for(i = 1; i < n; i++)
fxym[i] = 6 * f(i-1, i, i+1);
for(i = 1; i < n; i++)
a[i] = h[i-1] / (h[i] + h[i-1]);
c[i] = 1 - a[i];
a[n] = h[n-1] / (h[n-1] + h[n]);
cal_m(n);
cout<<"\\n输出三次样条插值函数:\\n";
printout(n);
cout<<"Do you to have anther try ? y/n :";
cin>>ch;
while(ch == 'y' || ch == 'Y');
return 0;
void printout(int n)
cout<<setprecision(6);
for(int i = 0; i < n; i++)
cout<<i+1<<": ["<<x[i]<<" , "<<x[i+1]<<"]\\n"<<"\\t";
/*
cout<<fxym[i]/(6*h[i])<<" * ("<<x[i+1]<<" - x)^3 + "<<<<" * (x - "<<x[i]<<")^3 + "
<<(y[i] - fxym[i]*h[i]*h[i]/6)/h[i]<<" * ("<<x[i+1]<<" - x) + "
<<(y[i+1] - fxym[i+1]*h[i]*h[i]/6)/h[i]<<"(x - "<<x[i]<<")\\n";
cout<<endl;*/
float t = fxym[i]/(6*h[i]);
if(t > 0)cout<<t<<"*("<<x[i+1]<<" - x)^3";
else cout<<-t<<"*(x - "<<x[i+1]<<")^3";
t = fxym[i+1]/(6*h[i]);
if(t > 0)cout<<" + "<<t<<"*(x - "<<x[i]<<")^3";
else cout<<" - "<<-t<<"*(x - "<<x[i]<<")^3";
cout<<"\\n\\t";
t = (y[i] - fxym[i]*h[i]*h[i]/6)/h[i];
if(t > 0)cout<<"+ "<<t<<"*("<<x[i+1]<<" - x)";
else cout<<"- "<<-t<<"*("<<x[i+1]<<" - x)";
t = (y[i+1] - fxym[i+1]*h[i]*h[i]/6)/h[i];
if(t > 0)cout<<" + "<<t<<"*(x - "<<x[i]<<")";
else cout<<" - "<<-t<<"*(x - "<<x[i]<<")";
cout<<endl<<endl;
cout<<endl;
2、程序比较复杂的:
(程序前面的01.,02.,03.等等为语句编号,实际应用时请一一删除)01./*=======================================================================*/
02.#include <stdio.h>
03.////////////////////////////////////////////////////////////////////////////////
04.#define MAXNUM 50 //定义样条数据区间个数最多为50个
05.typedef struct SPLINE //定义样条结构体,用于存储一条样条的所有信息
06. //初始化数据输入
07. float x[MAXNUM+1]; //存储样条上的点的x坐标,最多51个点
08. float y[MAXNUM+1]; //存储样条上的点的y坐标,最多51个点
09. unsigned int point_num; //存储样条上的实际的 点 的个数
10. float begin_k1; //开始点的一阶导数信息
11. float end_k1; //终止点的一阶导数信息
12. //float begin_k2; //开始点的二阶导数信息
13. //float end_k2; //终止点的二阶导数信息
14. //计算所得的样条函数S(x)
15. float k1[MAXNUM+1]; //所有点的一阶导数信息
16. float k2[MAXNUM+1]; //所有点的二阶导数信息
17. //51个点之间有50个段,func[]存储每段的函数系数
18. float a3[MAXNUM],a1[MAXNUM];
19. float b3[MAXNUM],b1[MAXNUM];
20. //分段函数的形式为 Si(x) = a3[i] * x(i+1) - x^3 + a1[i] * x(i+1) - x +
21. // b3[i] * x - x(i)^3 + b1[i] * x - x(i)
22. //xi为x[i]的值,xi_1为x[i+1]的值
23.SPLINE,*pSPLINE;
24.typedef int RESULT; //返回函数执行的结果状态,下面为具体的返回选项
25.#ifndef TRUE
26.#define TRUE 1
27.#endif
28.#ifndef FALSE
29.#define FALSE -1
30.#endif
31.#ifndef NULL
32.#define NULL 0
33.#endif
34.#ifndef ERR
35.#define ERR -2
36.#endif
37.//////////////////////////////////////////////////////////////////////////////////
38./*===============================================================================
39.*** 函数名称: Spline3()
40.*** 功能说明: 完成三次样条差值,其中使用追赶法求解M矩阵
41.*** 入口参数: (pSPLINE)pLine 样条结构体指针pLine中的x[],y[],num,begin_k1,end_k1
42.*** 出口参数: (pSPLINE)pLine 样条结构体指针pLine中的函数参数
43.*** 返回参数: 返回程序执行结果的状态TRUE or FALSE
44.================================================================================*/
45.RESULT Spline3(pSPLINE pLine)
46.
47. float H[MAXNUM] = 0; //小区间的步长
48. float Fi[MAXNUM] = 0; //中间量
49. float U[MAXNUM+1] = 0; //中间量
50. float A[MAXNUM+1] = 0; //中间量
51. float D[MAXNUM+1] = 0; //中间量
52. float M[MAXNUM+1] = 0; //M矩阵
53. float B[MAXNUM+1] = 0; //追赶法中间量
54. float Y[MAXNUM+1] = 0; //追赶法中间变量
55. int i = 0;
56. ////////////////////////////////////////计算中间参数
57. if((pLine->point_num < 3) || (pLine->point_num > MAXNUM + 1))
58.
59. return ERR; //输入数据点个数太少或太多
60.
61. for(i = 0;i <= pLine->point_num - 2;i++)
62. //求H[i]
63. H[i] = pLine->x[i+1] - pLine->x[i];
64. Fi[i] = (pLine->y[i+1] - pLine->y[i]) / H[i]; //求F[x(i),x(i+1)]
65.
66. for(i = 1;i <= pLine->point_num - 2;i++)
67. //求U[i]和A[i]和D[i]
68. U[i] = H[i-1] / (H[i-1] + H[i]);
69. A[i] = H[i] / (H[i-1] + H[i]);
70. D[i] = 6 * (Fi[i] - Fi[i-1]) / (H[i-1] + H[i]);
71.
72. //若边界条件为1号条件,则
73. U[i] = 1;
74. A[0] = 1;
75. D[0] = 6 * (Fi[0] - pLine->begin_k1) / H[0];
76. D[i] = 6 * (pLine->end_k1 - Fi[i-1]) / H[i-1];
77. //若边界条件为2号条件,则
78. //U[i] = 0;
79. //A[0] = 0;
80. //D[0] = 2 * begin_k2;
81. //D[i] = 2 * end_k2;
82. /////////////////////////////////////////追赶法求解M矩阵
83. B[0] = A[0] / 2;
84. for(i = 1;i <= pLine->point_num - 2;i++)
85.
86. B[i] = A[i] / (2 - U[i] * B[i-1]);
87.
88. Y[0] = D[0] / 2;
89. for(i = 1;i <= pLine->point_num - 1;i++)
90.
91. Y[i] = (D[i] - U[i] * Y[i-1]) / (2 - U[i] * B[i-1]);
92.
93. M[pLine->point_num - 1] = Y[pLine->point_num - 1];
94. for(i = pLine->point_num - 1;i > 0;i--)
95.
96. M[i-1] = Y[i-1] - B[i-1] * M[i];
97.
98. //////////////////////////////////////////计算方程组最终结果
99. for(i = 0;i <= pLine->point_num - 2;i++)
100.
101. pLine->a3[i] = M[i] / (6 * H[i]);
102. pLine->a1[i] = (pLine->y[i] - M[i] * H[i] * H[i] / 6) / H[i];
103. pLine->b3[i] = M[i+1] / (6 * H[i]);
104. pLine->b1[i] = (pLine->y[i+1] - M[i+1] * H[i] * H[i] / 6) /H[i];
105.
106. return TRUE;
107.
108.//////////////////////////////////////////////////////////////////////////////////
109.SPLINE line1;
110.pSPLINE pLine1 = &line1;
111.//////////////////////////////////////////////////////////////////////////////////
112.main()
113.
114. line1.x[0] = 27.7;
115. line1.x[1] = 28;
116. line1.x[2] = 29;
117. line1.x[3] = 30;
118. line1.y[0] = 4.1;
119. line1.y[1] = 4.3;
120. line1.y[2] = 4.1;
121. line1.y[3] = 3.0;
122. line1.point_num = 4;
123. line1.begin_k1 = 3.0;
124. line1.end_k1 = -4.0;
125. Spline3(pLine1);
126. return 0;
127.
128.//////////////////////////////////////////////////////////////////////////////////
插值-样条插值
百度百科定义
插值:在离散数据的基础上插补连续函数,使得这条连续曲线经过全部离散点,同时也可以估计出函数在其他点的近似值。
样条插值:一种以 可变样条 来作出一条经过一系列点的光滑曲线的数学方法。插值样条是由一些多项式组成的,每一个多项式都是由相邻的两个数据点决定的,这样,任意的两个相邻的多项式以及它们的导数在连接点处都是连续的。
样条插值法
简单理解,就是每两个点之间确定一个函数,这个函数就是一个样条,函数不同,样条就不同,所以定义中说 可变样条,然后把所有样条分段结合成一个函数,就是最终的插值函数。
思路1 - 线性样条
两点确定一条直线,我们可以在每两点间画一条直线,就可以把所有点连起来。
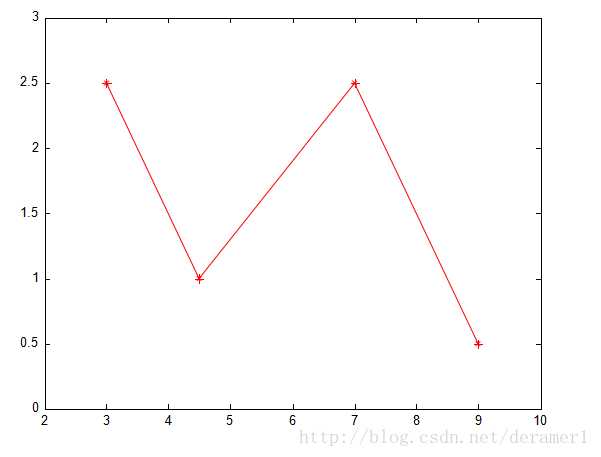
显然曲线不够光滑,究其原因是因为连接点处导数不相同。
思路2 - 二次样条
直线不行,用曲线代替,二次函数是最简单的曲线。
假设4个点,x0,x1,x2,x3,有3个区间,需要3个二次样条,每个二次样条为 ax^2+bx+c,故总计9个未知数。
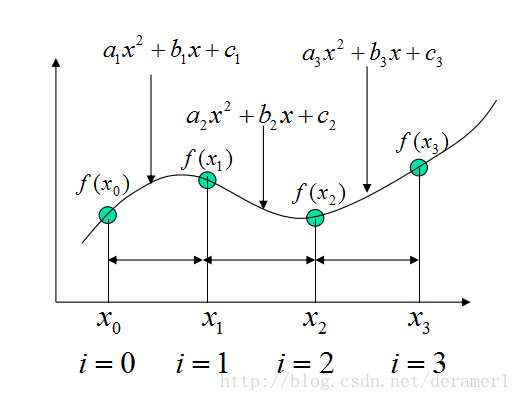
1. x0,x3两个端点都有一个二次函数经过,可确定2个方程
2. x1,x2两个中间点都有两个二次函数经过,可确定4个方程
3. 中间点处必须连续,需要保证左右二次函数一阶导相等
2*a1*x1+b1=2*a2*x1+b2
2*a2*x2+b2=2*a3*x2+b3
可确定2个方程,此时有了8个方程。
4. 这里假设第一方程的二阶导为0,即 a1=0,又是一个方程,共计9个方程。 【见补充】
联立即可求解。
python 实现
# encoding:utf-8 import numpy as np import matplotlib.pyplot as plt from pylab import mpl """ 二次样条实现 """ x = [3, 4.5, 7, 9] y = [2.5, 1, 2.5, 0.5] def calculateEquationParameters(x): #parameter为二维数组,用来存放参数,sizeOfInterval是用来存放区间的个数 parameter = [] sizeOfInterval=len(x)-1 i = 1 #首先输入方程两边相邻节点处函数值相等的方程为2n-2个方程 while i < len(x)-1: data = init(sizeOfInterval*3) data[(i-1)*3]=x[i]*x[i] data[(i-1)*3+1]=x[i] data[(i-1)*3+2]=1 data1 =init(sizeOfInterval*3) data1[i * 3] = x[i] * x[i] data1[i * 3 + 1] = x[i] data1[i * 3 + 2] = 1 temp=data[1:] parameter.append(temp) temp=data1[1:] parameter.append(temp) i += 1 #输入端点处的函数值。为两个方程,加上前面的2n-2个方程,一共2n个方程 data = init(sizeOfInterval*3-1) data[0] = x[0] data[1] = 1 parameter.append(data) data = init(sizeOfInterval *3) data[(sizeOfInterval-1)*3+0] = x[-1] * x[-1] data[(sizeOfInterval-1)*3+1] = x[-1] data[(sizeOfInterval-1)*3+2] = 1 temp=data[1:] parameter.append(temp) #端点函数值相等为n-1个方程。加上前面的方程为3n-1个方程,最后一个方程为a1=0总共为3n个方程 i=1 while i < len(x) - 1: data = init(sizeOfInterval * 3) data[(i - 1) * 3] =2*x[i] data[(i - 1) * 3 + 1] =1 data[i*3]=-2*x[i] data[i*3+1]=-1 temp=data[1:] parameter.append(temp) i += 1 return parameter """ 对一个size大小的元组初始化为0 """ def init(size): j = 0 data = [] while j < size: data.append(0) j += 1 return data """ 功能:计算样条函数的系数。 参数:parametes为方程的系数,y为要插值函数的因变量。 返回值:二次插值函数的系数。 """ def solutionOfEquation(parametes,y): sizeOfInterval = len(x) - 1 result = init(sizeOfInterval*3-1) i=1 while i<sizeOfInterval: result[(i-1)*2]=y[i] result[(i-1)*2+1]=y[i] i+=1 result[(sizeOfInterval-1)*2]=y[0] result[(sizeOfInterval-1)*2+1]=y[-1] a = np.array(calculateEquationParameters(x)) b = np.array(result) return np.linalg.solve(a,b) """ 功能:根据所给参数,计算二次函数的函数值: 参数:parameters为二次函数的系数,x为自变量 返回值:为函数的因变量 """ def calculate(paremeters,x): result=[] for data_x in x: result.append(paremeters[0]*data_x*data_x+paremeters[1]*data_x+paremeters[2]) return result """ 功能:将函数绘制成图像 参数:data_x,data_y为离散的点.new_data_x,new_data_y为由拉格朗日插值函数计算的值。x为函数的预测值。 返回值:空 """ def Draw(data_x,data_y,new_data_x,new_data_y): plt.plot(new_data_x, new_data_y, label=u"拟合曲线", color="black") plt.scatter(data_x,data_y, label=u"离散数据",color="red") mpl.rcParams[‘font.sans-serif‘] = [‘SimHei‘] mpl.rcParams[‘axes.unicode_minus‘] = False plt.title(u"二次样条函数") plt.legend(loc="upper left") plt.show() result=solutionOfEquation(calculateEquationParameters(x),y) new_data_x1=np.arange(3, 4.5, 0.1) new_data_y1=calculate([0,result[0],result[1]],new_data_x1) new_data_x2=np.arange(4.5, 7, 0.1) new_data_y2=calculate([result[2],result[3],result[4]],new_data_x2) new_data_x3=np.arange(7, 9.5, 0.1) new_data_y3=calculate([result[5],result[6],result[7]],new_data_x3) new_data_x=[] new_data_y=[] new_data_x.extend(new_data_x1) new_data_x.extend(new_data_x2) new_data_x.extend(new_data_x3) new_data_y.extend(new_data_y1) new_data_y.extend(new_data_y2) new_data_y.extend(new_data_y3) Draw(x,y,new_data_x,new_data_y)
可以看到 y 是多段二次函数拼接而成。
输出
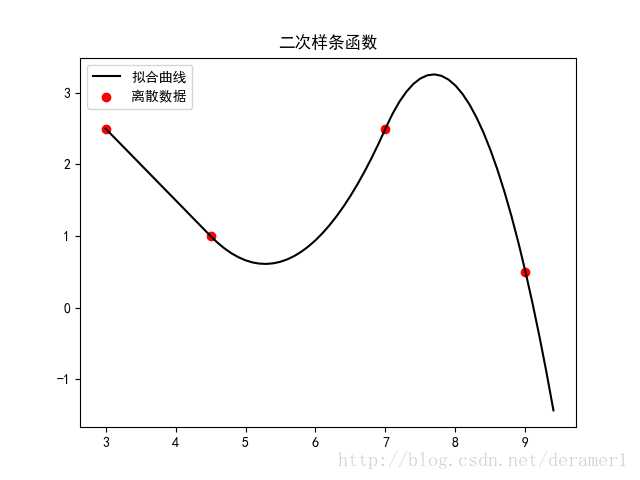
二次样条插值连续光滑,看起来效果还行。
只是前两个点之间是条直线,因为假设a1=0,二次函数变成b1x+c1,显然是直线;
而且最后两个点之间过于陡峭 。
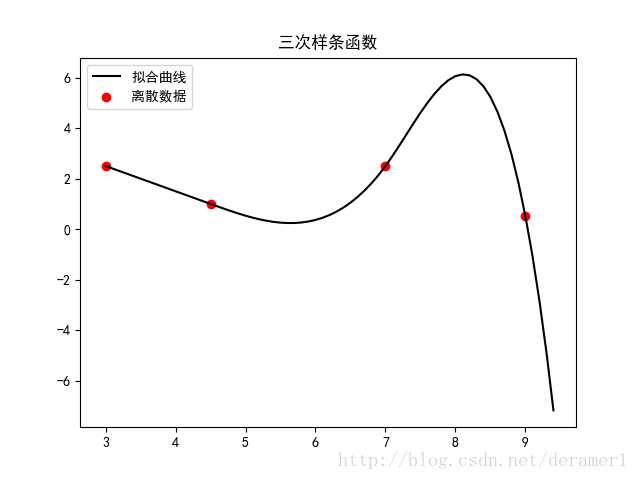
思路3 - 三次样条
二次函数最高项系数为0,导致变成直线,那三次函数最高项系数为0,还是曲线,插值效果应该更好。
三次样条思路与二次样条基本相同,
同样假设4个点,x0,x1,x2,x3,有3个区间,需要3个三次样条,每个三次样条为 ax^3+bx^2+cx+d,故总计12个未知数。
1. 内部节点处的函数值应该相等,这里一共是4个方程。
2. 函数的第一个端点和最后一个端点,应该分别在第一个方程和最后一个方程中。这里是2个方程。
3. 两个函数在节点处的一阶导数应该相等。这里是两个方程。
4. 两个函数在节点处的二阶导数应该相等,这里是两个方程。 【见补充】
5. 假设端点处的二阶导数为零,这里是两个方程。 【见补充】
a1=0
b1=0
python 实现
# encoding:utf-8 import numpy as np import matplotlib.pyplot as plt from pylab import mpl """ 三次样条实现 """ x = [3, 4.5, 7, 9] y = [2.5, 1, 2.5, 0.5] def calculateEquationParameters(x): #parameter为二维数组,用来存放参数,sizeOfInterval是用来存放区间的个数 parameter = [] sizeOfInterval=len(x)-1; i = 1 #首先输入方程两边相邻节点处函数值相等的方程为2n-2个方程 while i < len(x)-1: data = init(sizeOfInterval*4) data[(i-1)*4] = x[i]*x[i]*x[i] data[(i-1)*4+1] = x[i]*x[i] data[(i-1)*4+2] = x[i] data[(i-1)*4+3] = 1 data1 =init(sizeOfInterval*4) data1[i*4] =x[i]*x[i]*x[i] data1[i*4+1] =x[i]*x[i] data1[i*4+2] =x[i] data1[i*4+3] = 1 temp = data[2:] parameter.append(temp) temp = data1[2:] parameter.append(temp) i += 1 # 输入端点处的函数值。为两个方程, 加上前面的2n - 2个方程,一共2n个方程 data = init(sizeOfInterval * 4 - 2) data[0] = x[0] data[1] = 1 parameter.append(data) data = init(sizeOfInterval * 4) data[(sizeOfInterval - 1) * 4 ] = x[-1] * x[-1] * x[-1] data[(sizeOfInterval - 1) * 4 + 1] = x[-1] * x[-1] data[(sizeOfInterval - 1) * 4 + 2] = x[-1] data[(sizeOfInterval - 1) * 4 + 3] = 1 temp = data[2:] parameter.append(temp) # 端点函数一阶导数值相等为n-1个方程。加上前面的方程为3n-1个方程。 i=1 while i < sizeOfInterval: data = init(sizeOfInterval * 4) data[(i - 1) * 4] = 3 * x[i] * x[i] data[(i - 1) * 4 + 1] = 2 * x[i] data[(i - 1) * 4 + 2] = 1 data[i * 4] = -3 * x[i] * x[i] data[i * 4 + 1] = -2 * x[i] data[i * 4 + 2] = -1 temp = data[2:] parameter.append(temp) i += 1 # 端点函数二阶导数值相等为n-1个方程。加上前面的方程为4n-2个方程。且端点处的函数值的二阶导数为零,为两个方程。总共为4n个方程。 i = 1 while i < len(x) - 1: data = init(sizeOfInterval * 4) data[(i - 1) * 4] = 6 * x[i] data[(i - 1) * 4 + 1] = 2 data[i * 4] = -6 * x[i] data[i * 4 + 1] = -2 temp = data[2:] parameter.append(temp) i += 1 return parameter """ 对一个size大小的元组初始化为0 """ def init(size): j = 0 data = [] while j < size: data.append(0) j += 1 return data """ 功能:计算样条函数的系数。 参数:parametes为方程的系数,y为要插值函数的因变量。 返回值:三次插值函数的系数。 """ def solutionOfEquation(parametes,y): sizeOfInterval = len(x) - 1 result = init(sizeOfInterval*4-2) i=1 while i<sizeOfInterval: result[(i-1)*2]=y[i] result[(i-1)*2+1]=y[i] i+=1 result[(sizeOfInterval-1)*2]=y[0] result[(sizeOfInterval-1)*2+1]=y[-1] a = np.array(calculateEquationParameters(x)) b = np.array(result) for data_x in b: print(data_x) return np.linalg.solve(a,b) """ 功能:根据所给参数,计算三次函数的函数值: 参数:parameters为二次函数的系数,x为自变量 返回值:为函数的因变量 """ def calculate(paremeters,x): result=[] for data_x in x: result.append(paremeters[0]*data_x*data_x*data_x+paremeters[1]*data_x*data_x+paremeters[2]*data_x+paremeters[3]) return result """ 功能:将函数绘制成图像 参数:data_x,data_y为离散的点.new_data_x,new_data_y为由拉格朗日插值函数计算的值。x为函数的预测值。 返回值:空 """ def Draw(data_x,data_y,new_data_x,new_data_y): plt.plot(new_data_x, new_data_y, label=u"拟合曲线", color="black") plt.scatter(data_x,data_y, label=u"离散数据",color="red") mpl.rcParams[‘font.sans-serif‘] = [‘SimHei‘] mpl.rcParams[‘axes.unicode_minus‘] = False plt.title(u"三次样条函数") plt.legend(loc="upper left") plt.show() result=solutionOfEquation(calculateEquationParameters(x),y) new_data_x1=np.arange(3, 4.5, 0.1) new_data_y1=calculate([0,0,result[0],result[1]],new_data_x1) new_data_x2=np.arange(4.5, 7, 0.1) new_data_y2=calculate([result[2],result[3],result[4],result[5]],new_data_x2) new_data_x3=np.arange(7, 9.5, 0.1) new_data_y3=calculate([result[6],result[7],result[8],result[9]],new_data_x3) new_data_x=[] new_data_y=[] new_data_x.extend(new_data_x1) new_data_x.extend(new_data_x2) new_data_x.extend(new_data_x3) new_data_y.extend(new_data_y1) new_data_y.extend(new_data_y2) new_data_y.extend(new_data_y3) Draw(x,y,new_data_x,new_data_y)
输出
补充
微分连续性
![]()
s 代表三次样条,s‘是一阶导,s‘‘是二阶导
端点条件
上面我们对端点处的样条进行了假设,为什么呢?其实端点可以有多种不同的限制,常见有3种。
自由边界 Natural
首尾两端没有受到任何使他们弯曲的力,二次样条就是 s’=0,三次样条就是 s‘‘=0
固定边界 Clamped
首尾两端点的微分值被指定
非节点边界 Not-A-Knot
把端点当做中间点处理,三次函数不做假设,即
![]()
![]()
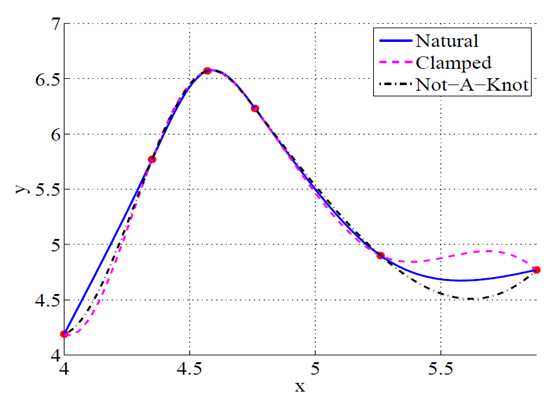
不同边界的比较
参考资料:
https://blog.csdn.net/flyingleo1981/article/details/53008931 三次样条插值(Cubic Spline Interpolation)及代码实现(C语言)
https://blog.csdn.net/deramer1/article/details/79034201 三次样条插值法
以上是关于Akima 插值和样条插值的C语言源代码,要有注释。的主要内容,如果未能解决你的问题,请参考以下文章