JDK 源码分析：快速排序算法

Posted 2021-04-05 程序大咖秀

快速排序简介

• 快速排序的时间复杂度为：最坏情况下是O( n2 )，平均情况是O( nlgn )。

下面是百度百科对快速排序算法的解释：

快速排序( Quick sort )是对冒泡排序的一种改进。
快速排序：由 C. A. R. Hoare 在 1962 年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

传统快速排序

假设需要对一个数组进行快速排序，数组元素为：6, 1, 2, 7, 9, 3, 4, 5, 10, 8。

选择一个基准数（如第一个元素：6），接下来的操作会以基准数为分界点，将比基准数小的元素放在其左边，大的放在其右边。

• 定义两个了游动下标i，j（犹如两个哨兵），让它们分别从序列两端开始 “扫描”（如下）；

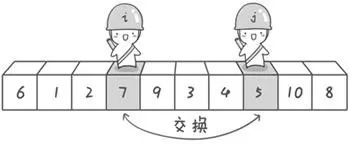
• 首先，哨兵j从右往左进行“扫描”，如果扫描到的元素大于基准数，则哨兵j继续往左走，直到探测到小于基准数的元素，则停下（此时，j指向的元素为5）；

  然后，哨兵i从左往右“扫描”，如果元素小于基准数，则哨兵i继续往右走，直到探测到大于基准数的元素，则停下（此时，i指向的元素为7）；

• 最后，将这两个哨兵所指向的元素进行交换；

  

  

  
  

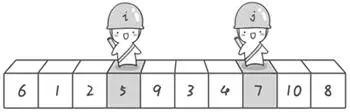
• 接下来，重复上述过程。哨兵j继续往左走，直到探测到小于基准数的元素，停下（此时，j指向的元素为4）；然后，哨兵i继续往右走，直到探测到大于基准数的元素，停下（此时，i指向的元素为9）；将这两个元素进行交换。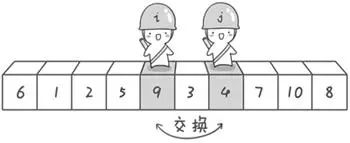

  

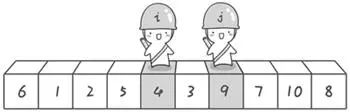
• 继续重复上述过程，直到两个哨兵碰面（指向同一位置），然后将基准数与两哨兵所指位置的元素进行交换；

  

  

  

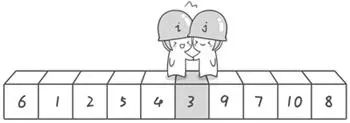
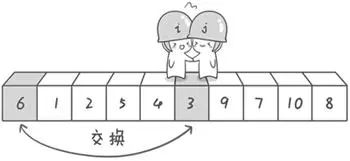
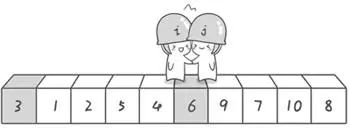
经过上述过程，我们就得到了以基准数为分界点的数组（两部分：小于基准数的部分左边，大于基准数的部分在右边）。

以此类推，分别对这两部分数据进行同样的快速排序操作，最终可得到排序后的序列。

JDK1.8 中的快速排序

在JDK1.7之前，都是使用传统的 Quicksort，但在JDK1.7及之后的版本中，使用的是DualPivotQuicksort算法，那这种优化算法与传统算法有什么区别吗？又是如何实现的呢？下面，小咖将对JAVA JDK1.8源码（详见java.util.DualPivotQuicksort类）中的快速排序算进行分析。

JDK1.8源码中定义了使用快速排序算法时的阈值：QUICKSORT_THRESHOLD，只有当待排序元素长度低于阈值时，使用快速排序；若超过，则使用其他排序算法。

1/**
2 * If the length of an array to be sorted is less than this
3 * constant, Quicksort is used in preference to merge sort.
4 */
5private static final int QUICKSORT_THRESHOLD = 286;

准备工作

1int[] a;                                    // 待排序数组（已初始化）
2int left = 0;                            // 左端下标位置
3int right = a.length - 1;      // 右端下标位置

首先，以数组中间位置为中心，取数组长度的七分之一为间距（经验值），从数组a中选取5个分位点，源码如下：

 1// 数组长度的 1/7 （近似值）
 2int seventh = (length >> 3) + (length >> 6) + 1;
 3
 4/*
 5 * Sort five evenly spaced elements around (and including) the
 6 * center element in the range. These elements will be used for
 7 * pivot selection as described below. The choice for spacing
 8 * these elements was empirically determined to work well on
 9 * a wide variety of inputs.
10 */
11int e3 = (left + right) >>> 1; // 中间位置
12int e2 = e3 - seventh;
13int e1 = e2 - seventh;
14int e4 = e3 + seventh;
15int e5 = e4 + seventh;

然后分别对这5个分位点所指向的元素进行升序排列（排序后:a[e1]<=a[e2]<=a[e3]<=a[e4]<= a[e5]），源码如下：

 1// 使用直接插入排序
 2if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; }
 3
 4if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t;
 5    if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
 6}
 7if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t;
 8    if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
 9        if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
10    }
11}
12if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t;
13    if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t;
14        if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t;
15            if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; }
16        }
17    }
18}

选取分位点之后，数组的结构划分大致是这样的：

待排序序列划分

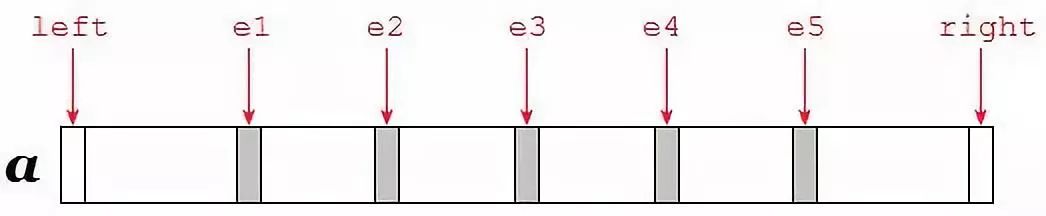
接下来，分别针对不同的情况，使用相应的策略进行快速排序。

若上述5个分位点 相邻位置的元素都不相同，则使用 双枢轴快速排序，否则使用 单枢轴快速排序。

1// 定义了两个游动的下标（可看做两个哨兵）
2int less  = left;
3int great = right;
4 
5if (a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]) {
6    // TODO: 双枢轴快速排序
7} else {
8    // TODO: 单枢轴快速排序
9}

双枢轴快速排序

顾名思义，是要选取两个枢轴（pivot1、pivot2）。显然，两个枢轴最终可以将数组划分为三个部分：第一部分是小于pivot1的所有元素，第二部分是在pivot1与 pivot2之间的所有元素，第三部分是大于pivot2的所有元素（如下）。

1*         left part                                   center part                         right part
2* +---------------------------------------------------------------+
3* |      < pivot1     |       pivot1 <= && <= pivot2      |       ?       |     > pivot2     |
4* +---------------------------------------------------------------+
5*                             ^                                                             ^        ^
6*                             |                                                             |        |
7*                          less                                                          k    great

画个示意图就是：

期望得到的序列结构

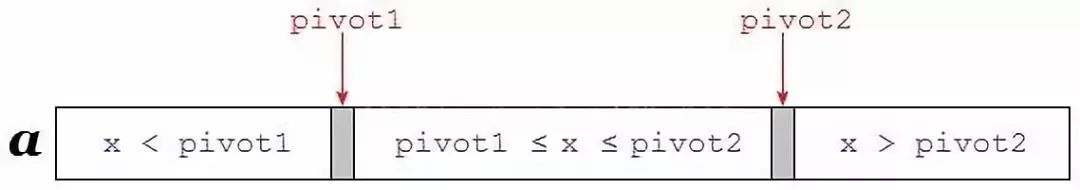
那具体是如何做到的呢？请跟着小咖阅读源码：

 1// 选分位点 e2, e4 作为两个枢轴，分别记作：pivot1, pivot2
 2int pivot1 = a[e2];
 3int pivot2 = a[e4];
 4
 5// 将待排序元素的第一个和最后一个元素分别放在枢轴位置
 6a[e2] = a[left];
 7a[e4] = a[right];
 8
 9// 跳过左端比 pivot1 小的元素，右端比 pivot2 大的元素
10while (a[++less] < pivot1);
11while (a[--great] > pivot2);

可得到如下的数组结构：

1*             left part                        center part                         right part
2* +----------------------------------------------------------------+
3* |         < pivot1           |                       ?                      |              > pivot2            |
4* +----------------------------------------------------------------+
5*                                      ^                      ^                       ^
6*                                      |                      |                       |
7*                                   less                   k                   great

简要的来说，双枢轴快速排序算法就是：利用k ∈ [less, great]进行“扫描”，随着k向右移动，将区间内的所有元素移动到正确的位置，此过程中less与great的位置也在动态的调整（如下图）。

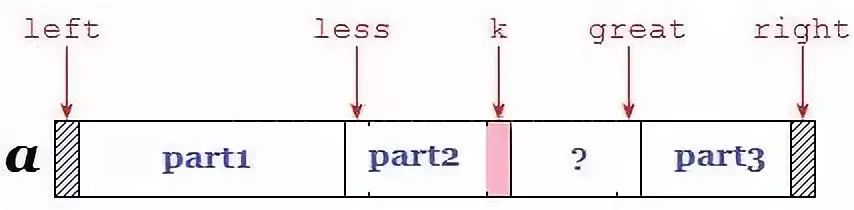
JDK1.8源码实现如下（分析详见注释）：

 1// 双枢轴快速排序：判断 [less, great] 区间内的元素
 2outer:
 3for (int k = less - 1; ++k <= great; ) { 
 4    int ak = a[k];
 5    if (ak < pivot1) {                         // 小于 pivot1 的移动到 less 的左边（交换）
 6        a[k] = a[less];
 7        a[less] = ak;
 8        ++less;                                      // 同时 less 位置往右挪动一位
 9    } else if (ak > pivot2) {
10        while (a[great] > pivot2) {  // 跳过比 pivot2 大的元素
11            if (great-- == k) {
12                break outer;
13            }
14        }
15
16        if (a[great] < pivot1) {        // 小于 pivot1 的元素移动到 less 的左边
17            a[k] = a[less];
18            a[less] = a[great];
19            ++less;                                 // 同时 less 位置往右挪动一位
20        } else {
21            a[k] = a[great];                 // pivot1 <= a[great] <= pivot2
22        }
23
24        a[great] = ak;                        // 大于 pivot2 的元素移动到 great 的左边
25        --great;                                  // 同时 great 位置往左挪动一位
26    }
27}
28
29// 交换枢轴元素值
30a[left]  = a[less  - 1]; a[less  - 1] = pivot1;
31a[right] = a[great + 1]; a[great + 1] = pivot2;
32
33// 对 [left, less -2] 与 [great - 2, right] 之间的元素进行排序
34sort(a, left, less - 2, leftmost);
35sort(a, great + 2, right, false);
36
37// 对于中间部分 [less - 1, great + 1] 区间的元素
38if (less < e1 && e5 < great) {      // 若中间部分元素太多(超过数组长度的 4/7)
39    while (a[less] == pivot1) {    // 跳过左端与 pivot1 相等的元素
40        ++less;
41    }       
42    while (a[great] == pivot2) {  // 跳过右端与 pivot2 相等的元素
43        --great;
44    }     
45
46    outer:
47    for (int k = less - 1; ++k <= great; ) {
48        int ak = a[k];
49        if (ak == pivot1) {               // 将与 pivot1 相等的元素挪到 less 的左边
50            a[k] = a[less];
51            a[less] = ak;
52            ++less;                               // 同时 less 向右移一位   
53        } else if (ak == pivot2) {
54            while (a[great] == pivot2) {  // 跳过右端与 pivot2 相等的元素
55                if (great-- == k) {
56                    break outer;
57                }
58            }
59            if (a[great] == pivot1) {       // 将与 pivot1 相等的元素挪到 less 的左边
60                a[k] = a[less];
61                a[less] = pivot1;
62                ++less;                                  // 同时 less 向右移一位  
63            } else {                                      // pivot1 < a[great] < pivot2
64                a[k] = a[great];
65            }
66
67            a[great] = ak;          // 将与 pivot2 相等的元素挪到 great 的右边
68            --great;                    // 同时 great 向左移一位 
69        }
70    }
71}
72
73// 对调整后的中间部分进行排序
74sort(a, less, great, false);

实质上，上述代码描述的过程就是：

• 将小于pivot1的元素移动到第一部分，将大于pivot2的元素移动到第三部分，剩下的为第二部分：pivot1 <= 第二部分元素 <= pivot2；

• 当第二部分元素过多(超过数组长度的4/7)，则还需要对第二部分进行细分，即：将等于pivot1和等于pivot2的元素找出来放在第二部分的两端，则pivot1 < 剩余元素< pivot2（此举减少了要排序元素的数据量），如下图所示。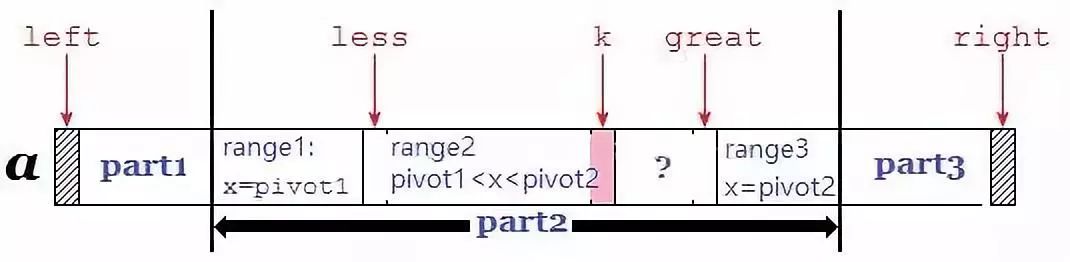

  

• 将第一部分元素，第三部分元素以及第二部分[less, great]之间的元素进行排序；

单枢轴快速排序

当5个分位点存在相邻位置元素相等的情况，则使用 单枢轴快速排序。显然，单枢轴快速排序 只选取一个枢轴，因此可将数组划分为两个部分。

JDK1.8 源码实现如下（分析详见注释）：

 1int pivot = a[e3];                  // 选分位点 e3 作为枢轴，记作：pivot
 2
 3for (int k = less; k <= great; ++k) {
 4    if (a[k] == pivot) {
 5        continue;
 6    }
 7    int ak = a[k];
 8    if (ak < pivot) {               // 小于 pivot 的元素移动到 less 的左边
 9        a[k] = a[less];
10        a[less] = ak;
11        ++less;                           // 同时 less 向右移
12    } else {
13        while (a[great] > pivot) {  // 跳过右边大于 pivot 的元素
14            --great;
15        }
16        if (a[great] < pivot) {        // 小于 pivot 的元素移动到 less 的左边
17            a[k] = a[less];
18            a[less] = a[great];
19            ++less;                               // 同时 less 向右移
20        } else {                                   // a[great] == pivot
21            a[k] = pivot;
22        }
23
24        a[great] = ak;                       // 大于 pivot 的元素移动到 great 的右边
25        --great;                                 // 同时 great 向左移
26    }
27}
28// 分别对得到的两部分进行排序
29sort(a, left, less - 1, leftmost);
30sort(a, great + 1, right, false);

实际上，上述代码描述的过程就是：

• 选取一个枢轴pivot，将小于pivot的元素放在less的左边，将大于pivot的元素放在great的右边，随着k往右“扫描”，less与great的值也随之调整，最终[less, great]之间就是pivot相等的元素；

单枢轴排序过程图

• 最后，[left, less -1]与[great + 1, right]这两部分元素进行排序。

参考资料：

1. DualPivotQuicksort：http://codeblab.com/wp-content/uploads/2009/09/DualPivotQuicksort.pdf

2. Why Is Dual-Pivot Quicksort Fast?：http://pdfs.semanticscholar.org/3478/a477919a34b30787c6a09b4b3afd038e97c1.pdf

---