红黑树

Posted 2021-04-04 数据结构与算法那些事儿

红黑树（二）

前言 

之前的一篇文章里重点讲了红黑树插入的知识，现在写的这篇文章则聚焦在红黑树的删除上。删除相较于插入来说，更困难一些，所以建议在已经学习插入的基础之上再学习删除会更容易理解一些。

红黑树

性质

（因为很重要，所以需要再回顾一下）

1. 红黑树的结点不是红色就是黑色；

2. 根的结点为黑色；

3. 所有的叶子结点都是黑色（这里的叶子结点是空结点）；

4. 每个红色的结点必须有两个黑色的子结点；

5. 从任何一个结点到其叶子结点的所有简单路径都包含相同数目的黑色结点；

红黑树的删除

首先，我们可以从5个性质可以推断得出：

• 性质1和性质3总是能够保持；

• 性质4只有在这些情况下才会触发：

• 增加红色结点；

• 将黑色结点重新绘制成红色结点；

• 旋转；

• 性质5只有在这些情况下才会触发：

• 增加黑色结点；

• 将红色结点重新绘制成黑色结点；

• 旋转

在BST中删除结点包括以下几种情况：

1. 该结点没有子结点，直接删除该结点即可；

2. 该结点其中一个子结点为空，则将存在的那一方的子结点替代掉该结点即可；

3. 删除结点的左右子结点均不为空，首先选择该结点的替代结点（可以是其左子树中的最大值，也可以是其右子树中的最小值，可以肯定的是替代结点必然最多只有一个子结点），接着将替代结点替换掉删除结点，同时把删除结点删掉，删掉后的结果则分为好几种情况（下面的结点为替代替代结点后的结点）：

1. 结点为新的根，此时只是将所有的路径中都去除一个黑色结点，所以依然保持平衡；

2. 结点的兄弟结点为红色；

3. 结点的兄弟结点为黑色，同时其子结点也均为黑色；

4. 结点的兄弟结点为黑色，同时兄弟结点的左子结点为红色，右子结点为黑色；

5. 结点的兄弟结点为黑色，同时兄弟结点的右子结点为红色，左子结点为红色；

接下来我们重点分析上面的第三种情况，因为这个是删除操作里面的核心操作。假设N为替换后的结点，P为N的父亲结点，S为N的兄弟结点，还有S左子结点为Sl和右子结点Sr，其中N为P的左子结点，S为右子结点；

3.1，因为子结点已经成为了新的根结点，满足所有条件；

3.2，因为删除后导致通过N的黑色结点减一，无法满足性质5，此时将兄弟结点染黑，父亲结点染红，接着对兄弟结点进行一个左旋转，旋转后如下图，变成了以S为相对根结点，P为红色左子结点的树，现在黑色结点的数目还是没有发生改变，不过可以发现的是，它变成了情况3；

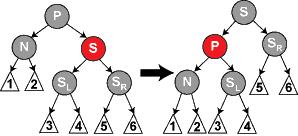
3.3，和上面同样的问题，将兄弟结点渲染成红色，导致结点 P两边的黑色结点数量均少了一，但是这会出现另一个问题－不通过P的比通过P的黑色结点的数量多一，此时则需要往上递归，将结点P从情况一开始判断；

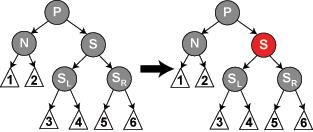
3.4，（假设情况4跟情况5均是当前结点为父亲结点的左子结点的情况）此时兄弟结点为父亲结点的右子结点，形成一个右左的形状，接着要对S进行一个右旋转，变成了情况5，如下图：

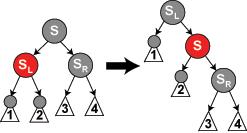
3.5，此时是一个右右的形状，进行一个左旋即可，需要注意的是，在示意图中的白色节点可以是红色或黑色，但是在变换前后都必须指定相同的颜色，可以发现此时满足所有情况；

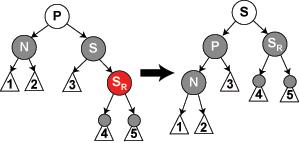
删除的实现

同样的，我们先看核心的操作，左旋和右旋；

左旋：

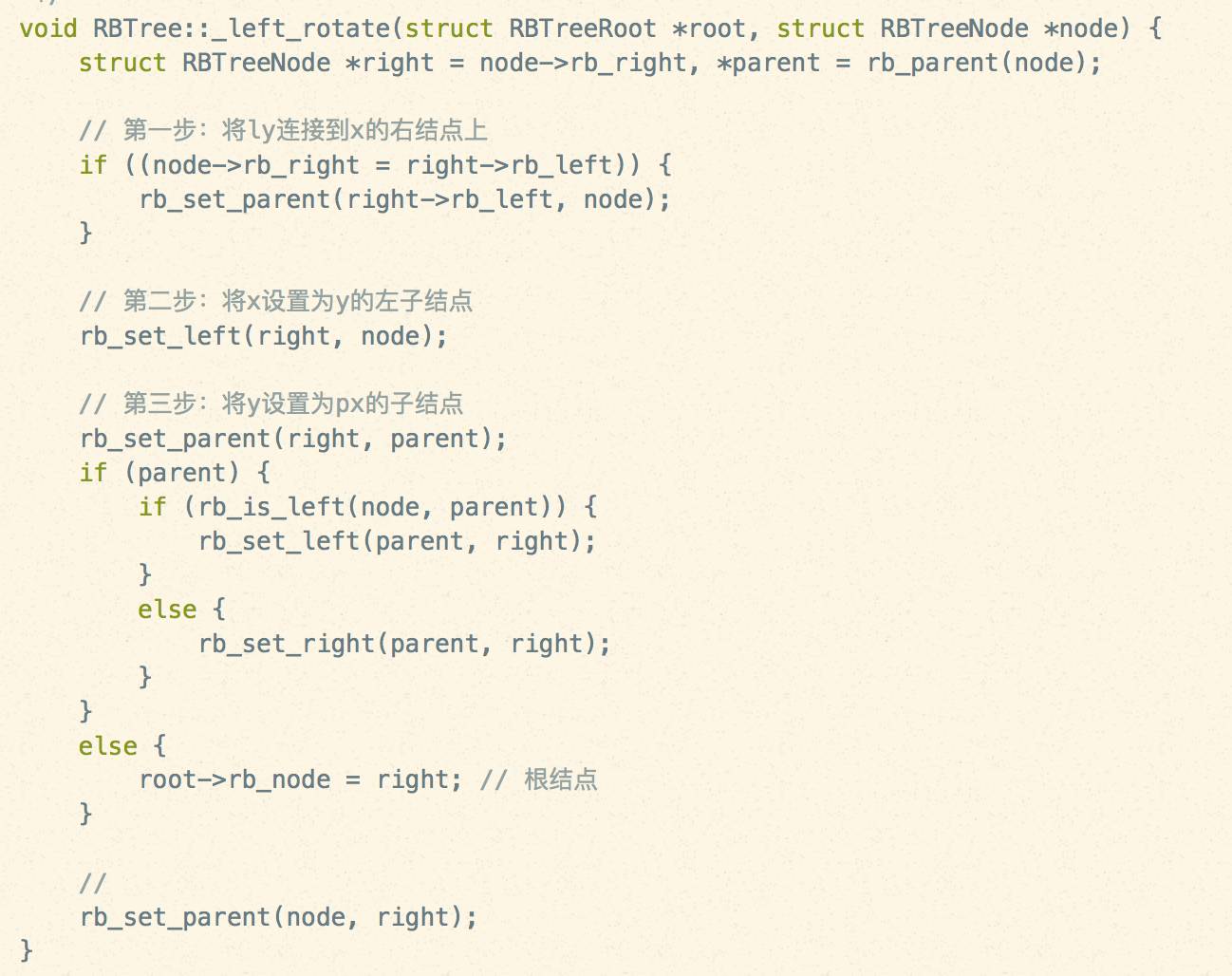
右旋：

在了解两个基本操作以后，接下来我们首先要对删除结点进行操作（代码有点长，所以只看其中重点部分）

下面则是有双子结点的情况：

接下来就是要处理替代结点被删除以后的情况了，就像我们所说的，分为好几种情况：先看没有进行旋转的操作

再来看需要进行旋转的操作（也就是后面两种情况）

上面的代码只是当前结点为父亲结点的左子结点的情况，当然还包括当前结点为父亲结点的右子结点的情况，不过原理大致是相通的，可以参考平衡二叉树将涉及方向的操作反过来即可。

注意事项

最后两种情况中，情况4中对兄弟结点进行的旋转；而情况5中则对一开始兄弟结点的父亲结点进行的旋转，还有并不需要关心情况5中父亲结点的颜色，只需要保证左边数量加一，右边数量不变即可；

还有一点就是在处理完操作以后，需要将根结点的颜色置为黑色。

下篇文章预告

哈希算法