JAVA中的数据结构 - 真正的去理解红黑树

Posted 2021-04-04 包子的实验室

一， 红黑树所处数据结构的位置：

在JDK源码中, 有treeMap和JDK8的HashMap都用到了红黑树

二，红黑树特性，以及保持的手段

1，根和叶子节点都是黑色的

2，不能有有连续两个红色的节点

3， 从任一节点到它所能到达得叶子节点的所有简单路径都包含相同数目的黑色节点

满足这几个特性就是一颗2-3-4的B树了，从而满足了O(logn)查找效率

通过下面这些操作可以理解成2-3-4树的向上增长的过程，包括

1， 改变颜色

2， 左旋

3， 右旋

三，从JDK源码来理解

先看TreeMap

//对treeMap的红黑树理解注解. 2017.02.16 by 何锦彬  JDK,1.7.51<br>  <br>/** From CLR */
    private void fixAfterInsertion(Entry<K, V> x) { 
         
         
        //新加入红黑树的默认节点就是红色
        x.color = RED;        /**         * 1. 如为根节点直接跳出         */
        while (x != null && x != root && x.parent.color == RED) {            
            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {                 
                //如果X的父节点（P）是其父节点的父节点（G）的左节点 
                //即 下面这种情况
                /**                 *                         G                 *               P(RED)              U                 */              
                //获取其叔(U)节点
                Entry<K, V> y = rightOf(parentOf(parentOf(x)));                if (colorOf(y) == RED) {                    // 这种情况，对应下面 图：情况一
                    /**                     *                         G                     *               P(RED)              U(RED)                     *          X                     */
                    //如果叔节点是红色的（父节点有判断是红色）. 即是双红色，比较好办，通过改变颜色就行. 把P和U都设置成黑色然后,X加到P节点。 G节点当作新加入节点继续迭代
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {                    //处理红父，黑叔的情况
                    if (x == rightOf(parentOf(x))) {                        // 这种情况，对应下面 图：情况二
                        /**                         *                           G                         *            P(RED)                        U(BLACK)                         *                     X                         */
                        //如果X是右边节点
                        x = parentOf(x);                        // 进行左旋
                        rotateLeft(x);
                    }                    //左旋后，是这种情况了，对应下面 图：情况三
                    /**                     *                           G                     *            P(RED)                        U(BLACK)                     *      X                     */
                     
                    // 到这，X只能是左节点了，而且P是红色，U是黑色的情况
                    //把P改成黑色，G改成红色，以G为节点进行右旋
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateRight(parentOf(parentOf(x)));
                }
            } else {                //父节点在右边的
                /**                 *                         G                 *                 U               P(RED)                 */              
                //获取U
                Entry<K, V> y = leftOf(parentOf(parentOf(x)));                 
                if (colorOf(y) == RED) {                    //红父红叔的情况
                    /**                     *                          G                     *             U(RED)               P(RED)                     */    
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);                    //把G当作新插入的节点继续进行迭代
                    x = parentOf(parentOf(x));
                } else {                    //红父黑叔，并且是右父的情况
                    /**                     *                          G                     *             U(RED)               P(RED)                     */    
                    if (x == leftOf(parentOf(x))) {                    //如果插入的X是左节点
                     /**                        *                            G                        *            U(BLACK)                        P(RED)                        *                                       X                                      */
                        x = parentOf(x);                        //以P为节点进行右旋
                        rotateRight(x);
                    }                    //右旋后
                    /**                     *                            G                     *            U(BLACK)                        P(RED)                     *                                                        X                     */
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);                    //以G为节点进行左旋
                    rotateLeft(parentOf(parentOf(x)));
                }
            }
        }        //红黑树的根节点始终是黑色
        root.color = BLACK;
    }

 

再看看HashMap的实现，

在HashMap中，在JDK8后开始用红黑树代替链表，查找由O(n) 变成了 O(Logn)

源码分析如下:

for (int binCount = 0; ; ++binCount) {                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);                        //JDK8 的hashmap，链表到了8就需要变成颗红黑树了
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);                        break;
                    }

//hashmap的红黑树平衡
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root，TreeNode<K,V> x) {

情况图

                      情况1

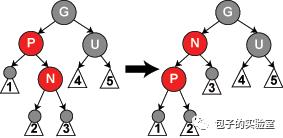
                      情况2

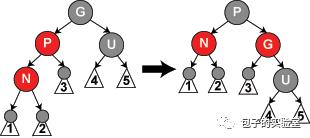
                         情况3

JDK源码处理红黑树的流程图

三，个人对红黑树理解的方法

1, 如何理解红黑树的O(lgN)的特性？

从2-3-4树去理解

红黑树，其实是一颗 2-3-4的B树，B树都是向上增长的，如果不理解向上增长可以先看看2-3树，这样理解就能知道为什么能O（lgn）的查找了

 

2, 如何理解红黑树的红黑节点意义？

可以把红色节点看成是连接父节点的组成的一个大节点(2个或3个或4个节点组成的一个key)，如下:

红色的就是和父节点组成了大节点

比如 

节点7和6，6是红色节点组成，故和它父节点7组成了一个大节点，即 2-3-4树的 6, 7节点

3 , B树是如何保持O(lgn)的复杂度的呢?

 B+树都是从底布开始往上生长，自动平衡，如 2-3-4树，当节点达到了3个时晋升到上个节点，所以不会产生单独生长一边的情况，形成平衡。

4， 数据库里的索引为什么不用红黑树而是用B+树（Mysql）呢？ 

后续解答