深入理解红黑树（RBT）

Posted 2021-04-04 睡到尘间饭熟时

红黑树（RBT）

基于BST存在的问题，一种新的树——平衡二叉查找树(Balanced BST)产生了。平衡树在插入和删除的时候，会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别为AVL树和红黑树。AVL树由于插入和删除性能差，在综合应用中不如红黑树。

红黑树的实际应用非常广泛，比如Linux内核中的完全公平调度器、高精度计时器、ext3文件系统等等，各种语言的函数库如Java的TreeMap和TreeSet，C++ STL的map、multimap、multiset等。

红黑树也是函数式语言中最常用的持久数据结构之一，在计算几何中也有重要作用。值得一提的是，Java 8中HashMap的实现也因为用RBTree取代链表，性能有所提升。

概念

红黑树需要满足的性质：

1.节点颜色非黑即红；

2.根节点是黑色；

3.父子节点之间不能出现两个连续的红节点

4.任何一个节点向下遍历到其子孙的叶子节点，所经过的黑节点个数必须相等；

5.空节点被认为是黑色的。

当查找树的结构发生改变时，红黑树的条件可能被破坏，需要通过调整使得查找树重新满足红黑树的条件。调整可以分为两类：一类是颜色调整，即改变某个节点的颜色；另一类是结构调整，集改变检索树的结构关系。结构调整过程包含两个基本操作：左旋（Rotate Left），右旋（RotateRight）。区分左旋和右旋的方法是：待旋转的节点从左边上升到父节点就是右旋，待旋转的节点从右边上升到父节点就是左旋。

 

红黑树的旋转

其实这里和avl的左旋和右旋是一样的，因为还有点蒙就再提一次。

左旋

左旋的过程是将x的右子树绕x逆时针旋转，使得x的右子树成为x的父亲，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

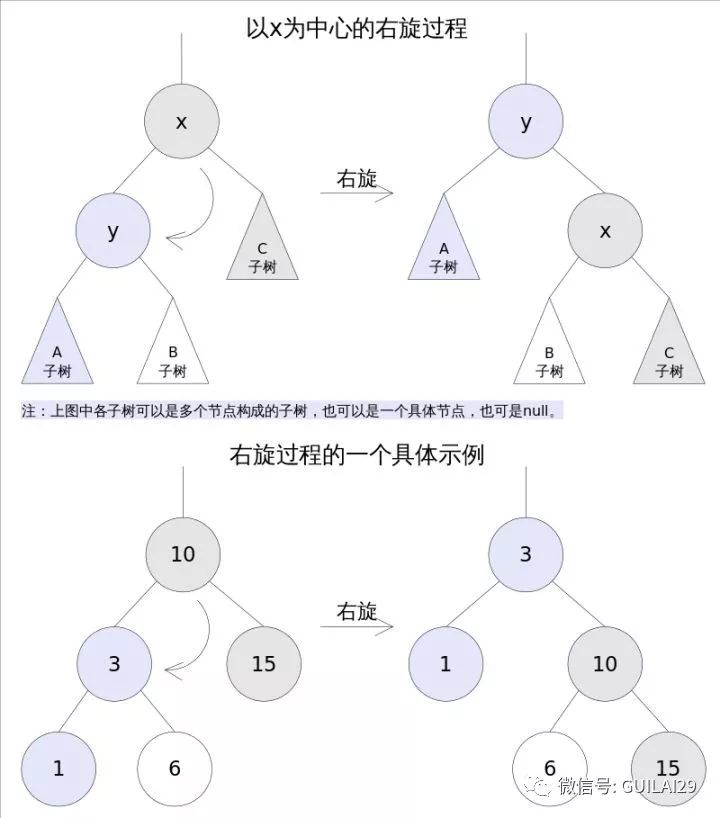
右旋

右旋的过程是将x的左子树绕x顺时针旋转，使得x的左子树成为x的父亲，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

 

红黑树的查找

查找操作也是和BST是一样的，大于根节点的查右子树，小于根节点的查左子树，进入左/右子树后可根据迭代或递归，直到找到相同的节点或全部查询完毕。

 

红黑树的插入

插入方式也与BST类似，只需要对树进行旋转操作和颜色修复，使其满足红黑树的定义。

新插入的节点是红色的，插入修复操作如果遇到父节点的颜色为黑则修复操作结束。也就是说，只有在父节点为红色节点的时候是需要插入修复操作的。

插入修复操作分为以下的三种情况，而且新插入的节点的父节点都是红色的：

1.叔叔节点也为红色。这种情况即将插入节点的父节点和叔叔节点与祖父节点的颜色互换，结束后如果A节点的父节点不是黑色的话，再继续做修复操作；

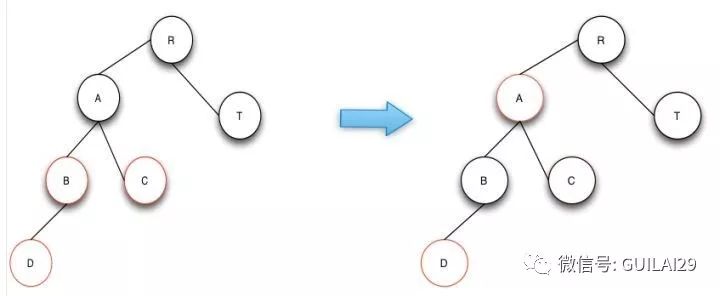
2.叔叔节点为空，且祖父节点、父节点和新节点处于一条斜线上。这种情况即需要将B点进行右旋，并且和B的父节点A互换颜色。当然如果B和C都是右节点的话，只要将操作变成左旋就可以了；

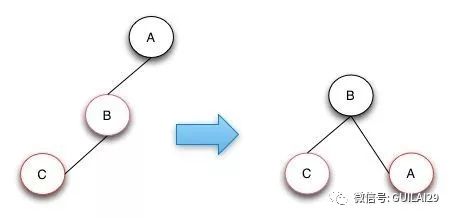
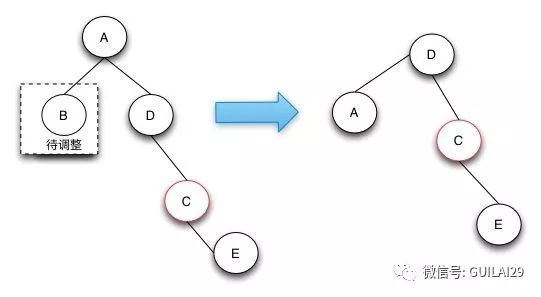
3.叔叔节点为空，且祖父节点、父节点和新节点不处于一条斜线上。如图只需要先将插入的C节点左旋，然后再针对其进行颜色修复即可。像与之相对应的镜像结构，只需将左旋变成右旋即可。

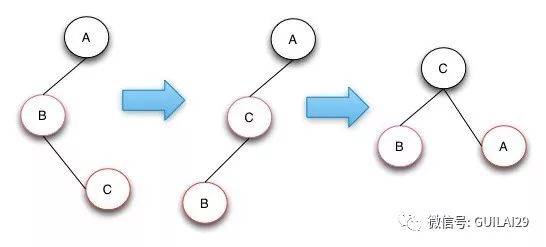
插入后的修复操作是一个向根节点回溯的操作，一旦牵涉的节点都符合了红黑树的定义，修复操作结束。之所以会向上回溯是由于case 1操作会将父节点，叔叔节点和祖父节点进行换颜色，有可能会导致祖父节点不平衡(红黑树定义3)。这个时候需要对祖父节点为起点进行调节（向上回溯）。

祖父节点调节后如果还是遇到它的祖父颜色问题，操作就会继续向上回溯，直到根节点为止，根据定义根节点永远是黑色的。在向上的追溯的过程中，针对插入的3中情况进行调节。直到符合红黑树的定义为止。直到牵涉的节点都符合了红黑树的定义，修复操作结束。而如果上面的3中情况如果对应的操作是在右子树上，直接做对应的镜像操作就是了。

到这里发现昨天会懵懵的原因是总想直接看整棵树，其实这种更应该先关注局部，再看整体，一点一点修复。

 

一个插入的例子

红黑树的删除

删除操作首先需要做的也是BST的删除操作，删除操作会删除对应的节点，如果是叶子节点就直接删除，如果是非叶子节点，会用对应的中序遍历的后继节点来顶替要删除节点的位置。删除后就需要做删除修复操作，使的树符合红黑树的定义，符合定义的红黑树高度是平衡的。

删除修复操作在遇到被删除的节点是红色节点或者到达根节点时，修复操作完毕。

删除修复操作是针对删除黑色节点才有的，当黑色节点被删除后会让整个树不符合红黑树的定义的第四条。需要做的处理是从兄弟节点上借调黑色的节点过来，如果兄弟节点没有黑节点可以借调的话，就只能往上追溯，将每一级的黑节点数减去一个，使得整棵树符合红黑树的定义。

删除操作的总体思想是从兄弟节点借调黑色节点使树保持局部的平衡，如果局部的平衡达到了，就看整体的树是否是平衡的，如果不平衡就接着向上追溯调整。

删除修复操作分为四种情况(删除黑节点后)：

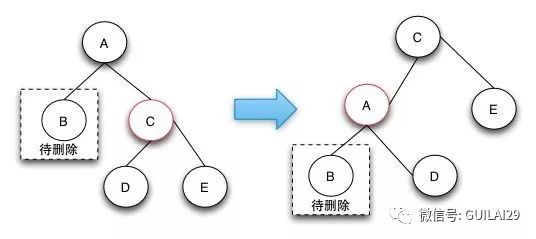
1.待删除的节点的兄弟节点是红色的节点。由于兄弟节点是红色节点的时候，无法借调黑节点，所以需要将兄弟节点提升到父节点，由于兄弟节点是红色的，根据RBTree的定义，兄弟节点的子节点是黑色的，就可以从它的子节点借调了。

case 1这样转换之后就会变成后面的case 2，case 3，或者case 4进行处理了。上升操作需要对C做一个左旋操作，如果是镜像结构的树只需要做对应的右旋操作即可。

之所以要做case 1操作是因为兄弟节点是红色的，无法借到一个黑节点来填补删除的黑节点。

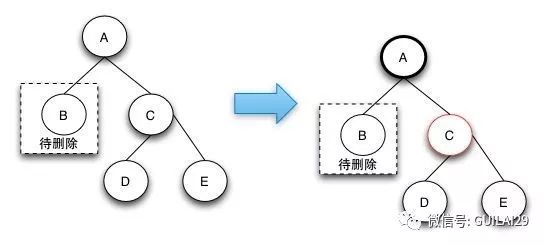
2.待删除的节点的兄弟节点是黑色的节点，且兄弟节点的子节点都是黑色的。case2的删除操作是由于兄弟节点可以消除一个黑色节点，因为兄弟节点和兄弟节点的子节点都是黑色的，所以可以将兄弟节点变红，这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点，继续向上调整，直到整颗树的颜色符合RBTree的定义为止。

case 2这种情况下之所以要将兄弟节点变红，是因为如果把兄弟节点借调过来，会导致兄弟的结构不符合RBTree的定义，这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后，达到了局部的平衡了，但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点，接着进行修复操作。

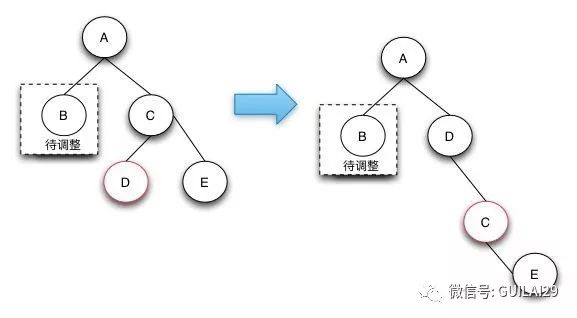
3.待调整的节点的兄弟节点是黑色的节点，且兄弟节点的左子节点是红色的，右节点是黑色的(兄弟节点在右边)，如果兄弟节点在左边的话，就是兄弟节点的右子节点是红色的，左节点是黑色的。

case 3的删除操作是一个中间步骤，它的目的是将左边的红色节点借调过来，这样就可以转换成case 4状态了，在case 4状态下可以将D，E节点都阶段过来，通过将两个节点变成黑色来保证红黑树的整体平衡。

之所以说case-3是一个中间状态，是因为根据红黑树的定义来说，下图并不是平衡的，他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况，是因为可以通过借用侄子节点的红色，变成黑色来符合红黑树定义4。

4.待调整的节点的兄弟节点是黑色的节点，且右子节点是是红色的(兄弟节点在右边)，如果兄弟节点在左边，则就是对应的就是左节点是红色的。

Case 4的操作是真正的节点借调操作，通过将兄弟节点以及兄弟节点的右节点借调过来，并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的，这样的话，整棵树还是符合红黑树的定义的。

Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑，且子节点不全部为黑，才有可能借调到两个节点来做黑节点使用，从而保持整棵树都符合红黑树的定义。

红黑树的删除操作是最复杂的操作，复杂的地方就在于当删除了黑色节点的时候，如何从兄弟节点去借调节点，以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的，这样只能通过选择操作让他上升到父节点，而由于它是红节点，所以它的子节点就是黑的，可以借调。

对于兄弟节点是黑色节点的可以分成3种情况来处理，当所以的兄弟节点的子节点都是黑色节点时，可以直接将兄弟节点变红，这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的，需要往上追溯继续调整。

对于兄弟节点的子节点为左红右黑或者 (全部为红，右红左黑)这两种情况，可以先将前面的情况通过选择转换为后一种情况，在后一种情况下，因为兄弟节点为黑，兄弟节点的右节点为红，可以借调出两个节点出来做黑节点，这样就可以保证删除了黑节点，整棵树还是符合红黑树的定义的，因为黑色节点的个数没有改变。

红黑树的删除操作是遇到删除的节点为红色，或者追溯调整到了根节点，这时删除的修复操作完毕。

总结

红黑树的插入和删除的操作比较难理解，这时要注意记住一点：操作之前红黑树是平衡的，颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色，要达到这个目的，就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转，一旦借调了别的节点，删除和插入的节点就会达到局部的平衡（局部符合红黑树的定义），但是被借调的节点就不会平衡了，这时就需要以被借调的节点为起点继续进行调整，直到整棵树都是平衡的。在整个修复的过程中，插入具体的分为3种情况，删除分为4种情况。

整个红黑树的查找，插入和删除都是O(logN)的，原因就是整个红黑树的高度是logN，查找从根到叶，走过的路径是树的高度，删除和插入操作是从叶到根的，所以经过的路径都是logN。

 

参考

https://www.jianshu.com/p/ad5d65e7ce62

https://www.zhihu.com/question/22774822

https://zhuanlan.zhihu.com/p/24367771

https://zhuanlan.zhihu.com/p/24795143?refer=dreawer

http://blog.csdn.net/eson_15/article/details/51144079

http://blog.csdn.net/sun_tttt/article/details/65445754

当前浏览器不支持播放音乐或语音，请在微信或其他浏览器中播放