算法导论第十三章 红黑树

Posted 2021-04-04 高性能服务器开发

写在前面

这一章真的把我害惨了，之前至少尝试看过3遍，每次看之前都下定决定一定要把它拿下，可是由于内容较多，深度够深，以致于每次要不是中途有什么事放弃了就跳过了，要不是花时间太多仍然不能理解而放弃。这次总算挺过来了，前后零零散散的时间加起来差不多也有两天时间。这次能坚持下来并攻克，我想大概有这么几个原因吧：第一是之前下定的决心要写一个最新版《算法导论》的读书笔记，之前几章都坚持写了，不能让这个成为拦路虎，即使再难再花时间都要弄懂；第二是通过前面几章的动手实践，发现自己的理解能力、动手能力都进步了，自然这章理解起来也不那么费力了；第三，如果有，那就是现在懂的东西多了，视野开阔了^-^。但说实话，也是费了不少心血，看了一下自己的打的草稿，超过十页以上，密密麻麻都是一些红黑树，这些努力我觉得都是值得的，但我之所以说“把我害惨了”，甚至有点不甘的是：我好大一部分时间都花在了调试代码上，原因是粗心大意写错了一些变量、指针……这一章由于涉及到多个指针的替换，所以切记在写的时候一定足够专注，尽量一口气写完，不要拖。

一、红黑树概览

      红黑树是一种平衡二叉树，什么是平衡二叉树？我的理解是加上”平衡条件“的二叉搜索树。其实这样的理解还不准确，因为二叉搜索树只在某些特殊的情况下是不平衡的。比如下图所示：

       所以，所谓树形平衡与否，并没有一个绝对的标准，”平衡“ 的大致意义是：没有任何一个结点深度过大。二叉搜索树在某些特殊情况下，无法维持绝对的平衡，所以，其动态集合操作，最坏的时间复杂度为O(n)。因此就出现一些通过加上某种”平衡条件“来促使二叉搜索树达到绝对的平衡（确保整棵树的深度维持在O(lgn)）。红黑树的”平衡条件“是：赋予结点不同颜色，并对根结点到任何叶子结点的颜色进行约束。这样的平衡不算太好，近似平衡，但性能已经比二叉搜索树提升了不少。
       红黑树不仅是二叉搜索树，且必须满足以下5条平衡规则：
1）每个结点或是红色，或是是黑色。
2）根结点是黑的。
3）所有的叶结点(NULL)是黑色的。（NULL被视为一个哨兵结点，所有应该指向NULL的指针，都看成指向了NULL结点。）
4）如果一个结点是红色的，则它的两个儿子节点都是黑色的。
5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
       简单的记法就是：红黑 黑 黑 红黑黑 黑
       黑高度的定义： 从某个结点出发(不包括该结点)到达一个叶结点的任意一条路径上，黑色结点的个数成为该结点x的黑高度。红黑树的黑高度定义为其根结点的黑高度。

二、平衡二叉树历史概览

三、红黑树实现

经验之谈：
1）插入删除和二叉搜索树类似，插入的结点必须着红色（因为如果是黑色，是一定会破坏性质5，难以修复，而如果是红色，则可能破坏性质2和4，容易修复）；
2）插入修复三种情况：发生在插入结点的父结点为红色的情况下，即破坏了性质4，这个时候考虑插入点的uncle结点进行修复；性质2破坏，直接着黑色；
3）删除恢复四种情况：发生在删除结点为黑色的情况下，即破坏了性质5，这个时候考虑删除点的brother结点进行修复；
4）旋转操作注意指针的指向，每个都要考虑全了，parent、left、right缺一不可。
       如果按照《算法导论》书的步骤一步步往下看，是一定看得懂的，因为书上的东西是写的最全的，网友写的博客虽然有些也不错，但都是经过自己过滤过的，且不说语言表达怎样，肯定没有书本记录得详细。只是有些地方书本上表达得太深奥，可以借助一些博客来理解。比如说我在看到删除修复的四种情况时，书上说的什么”双重黑色、红+黑，x既不是黑色，也不是红色“，把我搞得稀里糊涂的，看了之后整个人都不好了，后来看了July的博客才弄懂了个大概（见后面的参考引文），再回过头来看就发现原来如此。
       关于红黑树查找、删除等具体的细节就不再做过多的赘述，这里只记录下自己学习了之后的一些规律总结及心得。
关于旋转：
       旋转有些书分为单旋和双旋，双旋顾名思义就是单旋两次，单旋又分为左旋和右旋，操作是对称的。旋转操作对于理解树的指针指向是再好不过了，就像理解链表的指针指向再好不过是元素的插入了。这里要确保一个结点的三个指针：parent、left、right都要更新了。书上没说具体的方法论，如果让我们在纸上写个左旋，估计好多人都要跪，因为指针指来指去，没有思路完全不行。根据我的经验，总结这样的一个规律（仅供参考）：
就拿左旋作为例子，如下图所示：
规律可以总结成3个字：补——>提——>降
注意：图2由于纸张不够的原因，代码没写全，见下面的代码部分：

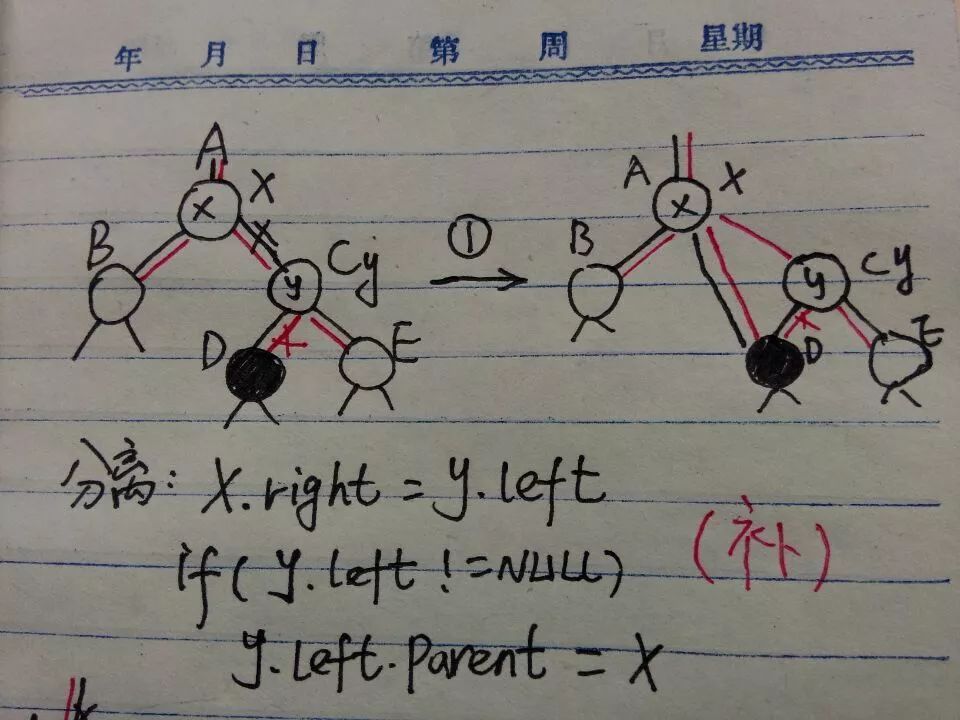
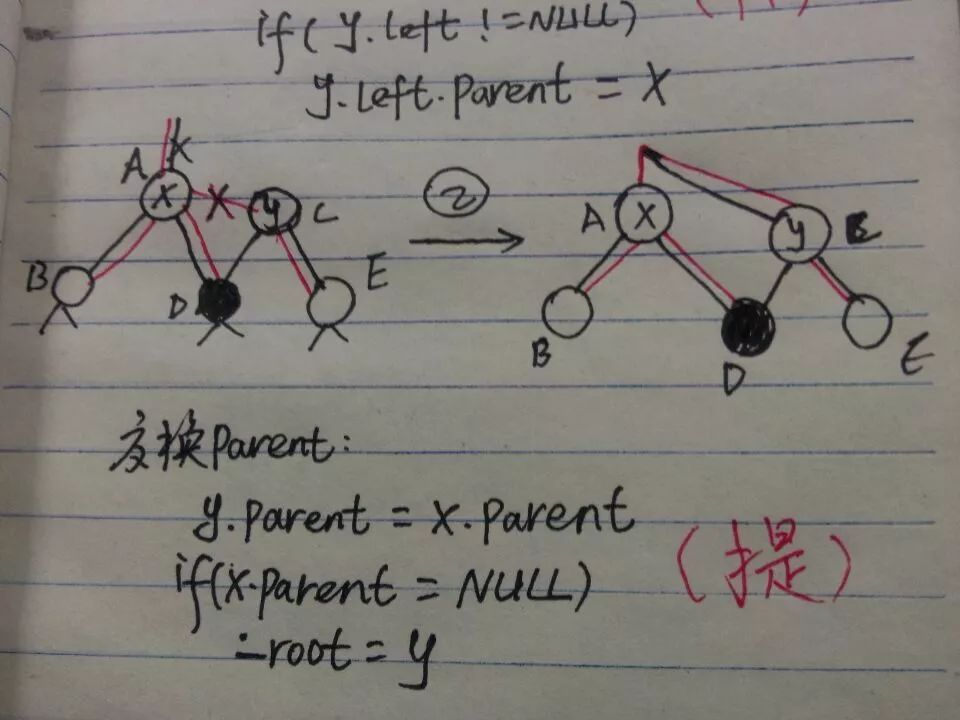
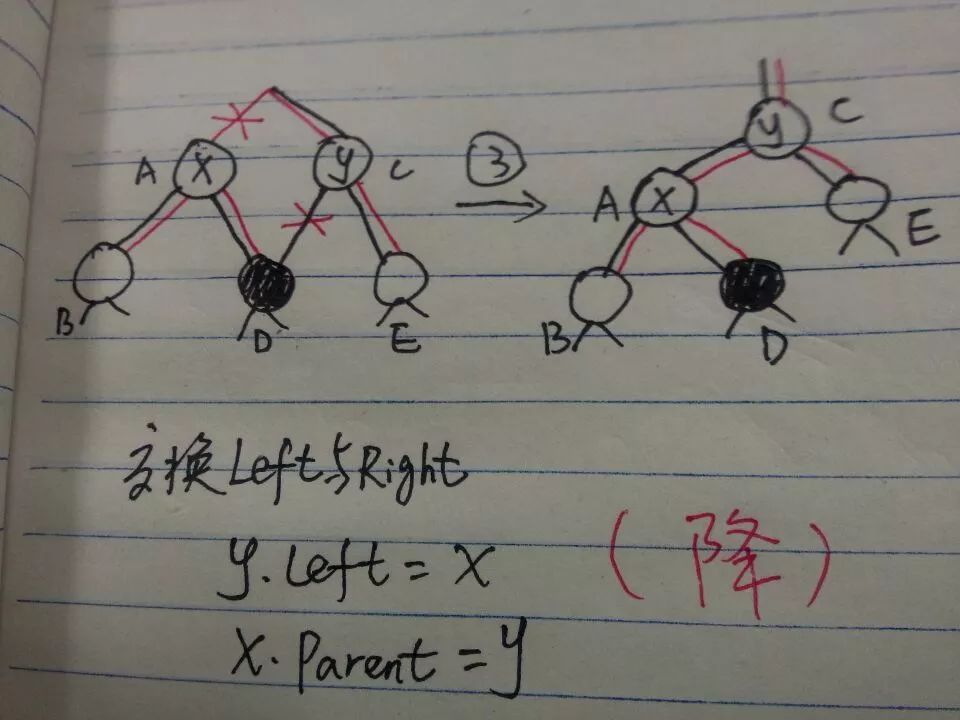
       附上左旋的代码（C++模板类）：

 1//左旋
 2template<typename TKey, typename TValue>
 3void RBTree<TKey, TValue>::_LeftRotate(RBTreeNode *x_node)
 4{
 5    //assert
 6    if (!(x_node->isValid() && x_node->Right->isValid()))
 7        throw exception("左旋操作要求对非哨兵进行操作，并且要求右孩子也不是哨兵");
 8    RBTreeNode *y_node = x_node->Right;
 91
10    //以下三步的宗旨是用 y 替换 x，注意将 x 的Parent、Left、Right都换成 y 的
11    // 1) x 和 y 分离 (补)
12    x_node->Right = y_node->Left;
13    if (y_node->Left != m_pNil)
14        y_node->Left->Parent = x_node;
151
16    // 2) 设置y->Parent (提)
17    y_node->Parent = x_node->Parent;
18    if (x_node->Parent == m_pNil)
19        m_pRoot = y_node;
20    else if (x_node->Parent->Left == x_node)
21        x_node->Parent->Left = y_node;
22    else
23        x_node->Parent->Right = y_node;
241
25    // 3) 设置y->Left (降)
26    y_node->Left = x_node;
27    x_node->Parent = y_node;
28}

关于删除修复的”双重黑、红+黑“：
       如何理解？这个地方，书上没说明白，在说这个意思之前，我们先来看看红黑树的删除修复究竟是怎么个回事？
       红黑树的删除务必不能破坏了红黑树的5条性质，但这是不可能的，如果删除的结点破坏了5条中任何一条性质，这个时候就需要采用措施进行修复，我们分析一下：删除什么结点会破坏性质，破坏哪条性质？
1）如果删除的是红色结点，则无影响；
2）如果删除的是黑色结点，则不用想，第5条性质破坏了，其中：
　　a）如果这个黑色结点是根结点，同时根结点的非空子结点，即将要替换它的结点为红色，则破坏性质2；
　　b）如果这个黑色结点的父结点和非空子结点都为红色，则破坏性质4。
       知道了这点，我们再来看下什么是”双重黑、红+黑“，其实，这个说法主要是一种假设，假设存在着这样的节点，那么红黑树的性质就满足了，但实际上这样的结点是不存在的，所以需要转换，而转换的过程就是修复的过程。说白了，这个假设是为了便于代码实现，为了方便完成四种修复操作的一个假设性规律。因为删除修复不像插入修复那么明显，有了它就像找到什么诀窍一样，删除的四种修复不用”强制性记忆“就能明白为什么要这样做^-^。
       红黑树的删除与二叉搜索树的删除基本一样，不同之处在于需要记录替换被删结点到那个结点，然后以它为根进行修复。”双重黑、红+黑“就体现在这里，如下两图所示：

       其中，delete结点被其后继结点 x （这里两种情况：一是后继就是delete的右孩子，二是比delete大的最小结点）替换。需要修复的条件是：删除结点得是黑色，如果 x 也是黑色，则称为”双黑“；如果 x 是红色，则称为”红黑“。好了，知道了这点，在对照着删除修复的四种情况看，就很容易懂了，其修复的过程就是看 x 的颜色情况和 x的兄弟结点的颜色情况，有双重黑的，就去掉一重黑，使之平衡，四种情况分别有不同的去重情况，整个过程是很好理解的，具体的细节就不做赘述，想必知道这点，整个删除修复就很好理解了。