聊聊红黑树

Posted 2021-04-04 究极饭团

之前就偶尔看过红黑树系列的文章，每次都是看完就忘，还是那句老话说的好，好记性不如烂笔头，这次就真真切切地就是想把红黑树的原理给写下来。经常用到的hashmap,treemap,treeset这些集合类也都是红黑树的应用。

首先红黑树是一棵二叉搜索树，它在每个节点上增加了一个存储位color来表示节点的颜色，可以是红色或者黑色，通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长于2倍，因而是近似于平衡的。所以红黑树是许多平衡搜索树中的一种，可以保证在最坏情况下基本动态集合操作（hashmap,treemap,treeset）的时间复杂度为O(lgn)。

性质

树中每个节点包含5个属性：color,key,left,right,和p。

叶节点

如果一个节点没有子节点或者父节点，则该节点相应指针属性的值为NIL。我们可以把这些NIL看做一个指向二叉搜索树的叶节点。为了便于处理红黑树代码中的边界条件，使用给一个哨兵T.nil来代表NIL。对于一颗红黑树T，哨兵T.nil是一个与树中普通节点有相同属性的对象。除了它的color属性为黑色之外，其他属性p,left,right,p可以设置为任何值。如下图：可以参照《算法导论》p175 13-1(b)

黑高

从某个节点x出发到达一个叶节点的任意一条简单路径上的黑色节点的个数称为该节点的黑高，红黑树黑高代表的是从根节点到每个叶节点的黑高都相同，于是红黑树的黑高也为其根节点的黑高。

五个红黑性质

一颗红黑树是满足下面红黑性质的二叉搜索树：

1. 每个节点或者是红色，或者是黑色。

2. 根节点是黑色的。

3. 每个叶节点（T.nil）是黑色的。

4. 如果一个节点是红色的，则它的两个子节点都是黑色的。

5. 对每一个节点，从该节点到其所有叶节点的简单路径上，均包含相同数目的黑色节点。这些相同数目的黑色节点的个数就是红黑树的黑高

旋转

旋转是在红黑树插入或者删除节点时必须要用到的一个关键操作，旋转分为左旋和右旋。

参考下图：可以参照《算法导论》p176 13-2

我们可以看下左旋的伪代码，假设x.right != nil。

建议在看代码的时候，可以一边看代码一边画图，画图有助于理解。

LEFT-ROTATE(T , x) {
    y = x.right             // 设置y为x的右子树
    x.right = y.left         // 把y的左子树转变成x的右子树
    if y.left != T.nil
        y.left.p = x
    y.p = x.p               // 把y的父节点设置为x的父节点
    if x.p == T.nil            // 这个ifelse的作用是用y节点代替x
        T.root = y           
    elseif x == x.p.left    
        x.p.left = y       
    else x.p.right = y       
    y.left = x               // 把x放到y的左节点 
    x.p = y                   
}

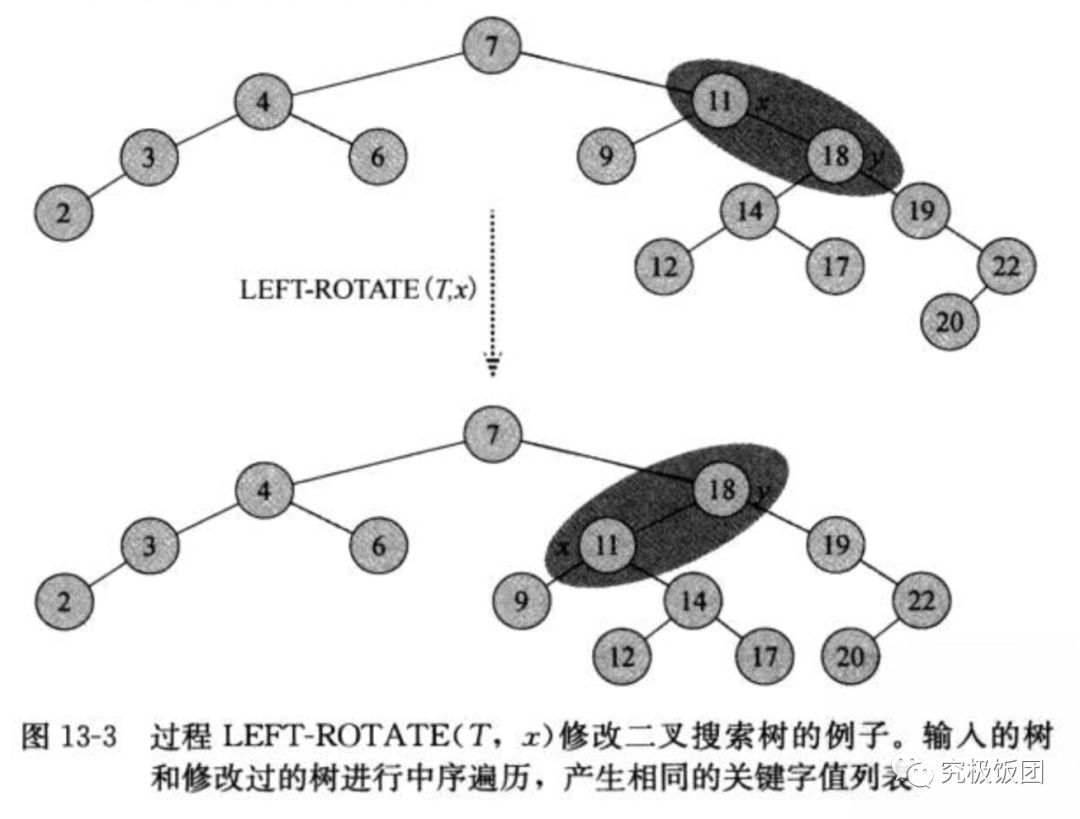
右旋操作的代码是和左旋代码对称的。左旋和右旋都是在O(1)时间内运行完成的。在旋转操作中，只有left,right,和p指针改变，其他所有属性都保持不变。

左旋参考下图：可以参照《算法导论》p177 13-3

插入

插入过程

我们可以在O(n)时间内完成向一颗含n个节点的红黑树中插入一个新节点。插入过程分两步：

1. 像插入二叉搜索树一样，把节点z插入插入树T内，并将z着色为红色，这个过程可能破坏红黑树的五条性质中的几条。

2. 对树中的节点重新着色并旋转以满足红黑树的五个性质。

我们将上述两个过程通过伪代码来实现:

第一步实现：RB-INSERT(T,z)

RB-INSERT(T , z){
    y = T.nil
    x = T.root
    while x != T.nil            // 这个while循环是为了找到z未来的父节点y
        y = x
        if z.key < x.key 
            x = x.left
        else x = x.right
    z.p = y
    if y == T.nil               // 找到父节点之后，要判断z应该是父节点y的左孩子还是右孩子
        T.root = z
    elseif z.key < y.key 
        y.left = z
    else y.right = z
    z.left = T.nil
    z.right = T.nil
    z.color = RED
    RB-INSERT-FIXUP(T,z)       // 这就是插入过程的第二步，对于z的插入可能导致的性质破坏，我们需要修复
}

第二步实现：RB-INSERT-FIXUP(T,z)

RB-INSERT-FIXUP(T , z){
    while z.p.color == RED {
        if z.p == z.p.p.left {
            y = z.p.p.left
            if y.color = RED
                z.p.color = BLACK                   // case 1
                y.color = BLACK                     // case 1
                z.p.p.color = RED                   // case 1   
                z = z.p.p                           // case 1
            elseif z == z.p.right
                z = z.p                             // case 2
                LEFT-ROTATE(T,z)                    // case 2
            else
                z.p.color = BLACK                   // case 3
                z.p.p.color = RED                   // case 3       
                RIGHT-ROTATE(T,z.p.p)               // case 3
        } else (same as then clause with "right" and "left" exchange)
    }
    T.root.color = BLACK
}

为了理解RB-INSERT-FIXUP的过程是如何实现的，我们要把代码分成三个主要的步骤去分析。

1. 首先，要确定当节点z被插入并着为红色之后，红黑性质中有哪些不能继续保持

2. 其次，代码中的while循环不变式是什么？

3. 最后，要分析while循环体中的三种情况

我们一个问题一个问题来攻破：

第一个问题，当节点z被插入并着为红色之后，红黑性质中有哪些不能继续保持呢？

性质1：因为新插入的节点被着为红色，所以性质1成立

性质2：如果z是根节点，根节点必须为黑色，而z节点又为红色，则破坏了性质2

性质3：因为新插入的红色节点的两个子节点都是哨兵T.nil，所以性质3继续成立

性质4：如果z的父节点是红节点则破坏了性质4

性质5：因为新插入的节点为红色，并不会影响红黑树的黑高，所以性质5也成立

所以通过上面的总结，性质2和性质4可能被破坏。

第二个问题，代码中的while循环不变式是什么？

在while循环中，每次迭代的开头保持了循环不变式，循环不变式在每一次迭代之前循环不变式为真，并且在循环终止时，这个循环不变式都会给出一个有用的性质，即5个性质都满足。

while循环在每次迭代的开头保持下列3个部分的不变式：

a. 节点z始终都是红色节点

b. 节点z的父节点z.p也始终为红色，如果z.p是黑色节点，则退出循环。

c. 如果有任何性质被破坏，则最多只有一个性质被破坏，要不就是性质2，要不就是性质4。

• 如果性质2被破坏，它的原因就是z是根节点，且是红节点，也是树内的唯一一个节点。则直接退出循环，并设置T.root.color = BLACK

• 如果性质4被破坏，它的原因是z和z.p都是红色节点。则会进入while循环中，考虑循环体内的六种情况。

相对于a部分和b部分，c部分是修复红黑性质4的问题，显得更是RB-INSERT-FIXUP保持红黑性质的中心内容。

随着循环的每次迭代，都保持着循环不变式，指针z会不断的沿着树向上移动，执行某些旋转之后循环终止。

第三个问题，while循环体中的六种情况是什么？

如果新节点不是树内唯一一个节点，即根节点的话，那么while循环体内解决的主要还是性质4的问题。但是因为不断解决性质4，而不断地把指针z上移动到根节点，那也会破坏性质2。性质4和性质2将会在循环体内解决

在循环体内实际上需要考虑到有六种情况，而其中三种与另外三种是对称的。这取决于z的父节点z.p是z的祖父节点z.p.p的左孩子还是右孩子。

然后对于其中的三种情况，case1，case2，case3的区别在于z.p的兄弟节点y(称为“叔节点”)的颜色不同。

• Case1：z的叔节点y是红色的

• Case2：z的叔节点y是黑色的且z是一个右孩子

• Case3：z的叔节点y是黑色的且z是一个左孩子

case1,case2,case3参考下图：可以参照《算法导论》p179 13-4

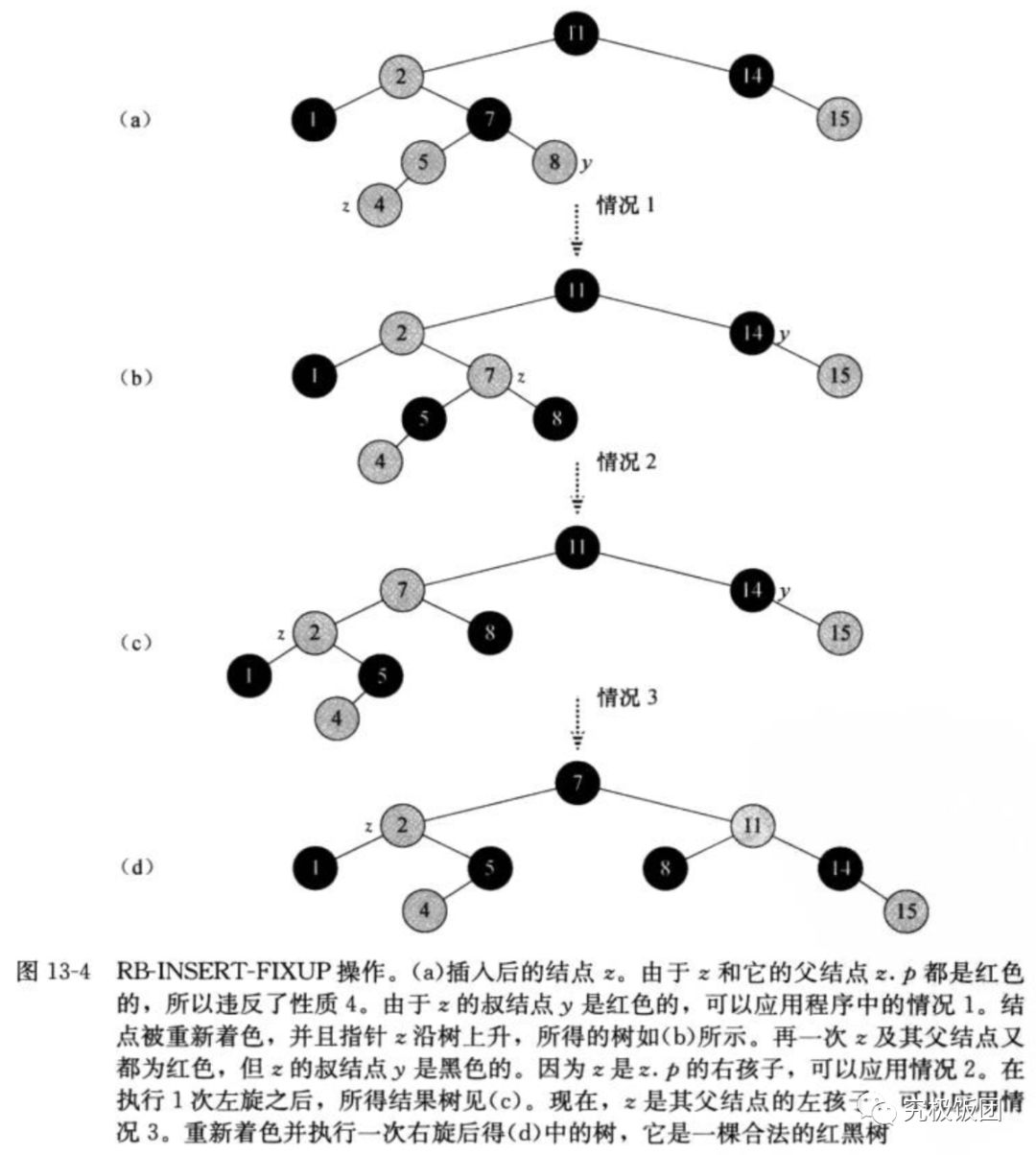
Case1：z的叔节点y是红色的

在case1中，z.p和y都是红色，根据性质4，则z.p.p肯定是黑色，所以将z.p和y都设为黑色，以解决z和z.p都是红色的性质4被破坏的问题，并把z.p.p设置为红色，以保持性质5不改变。并把z.p.p作为新节点z1来重复执行while循环。指针z在树中上移两层。

case1参考下图：可以参照《算法导论》p181 13-5

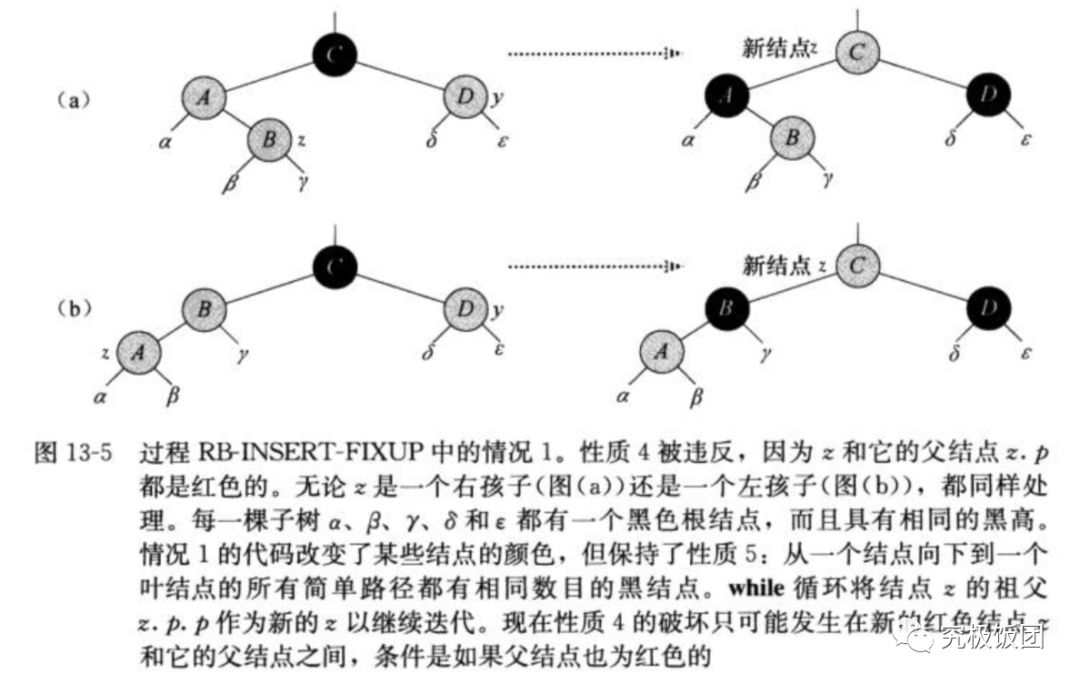
通过上面的变换之后，我们来看看while循环不变式有没有被破坏

a：因为这次迭代把z.p.p着为红色，新节点z1赋值为z.p.p，则z1在下次迭代时肯定也是红色，所以不变式a没问题.

b：由于z1.p是z.p.p.p，且这个节点的颜色并没有改变。如果z1.p是黑色，那将退出循环，如果是红色，那继续执行循环。

c：我们之前说了在case1中是保持了性质5，而且也不会引起性质1和性质3的变化。那么对于性质2和性质4呢?

• 性质2：如果节点z1在下次迭代开始时是根节点，case1修复了唯一被破坏的性质4，但由于z1是红色并且为根节点，则性质2被破坏了。由于z1.p为黑色，则会退出循环。

• 性质4：如果节点z1在下次迭代开始时不是根节点

• 如果z1.p是黑色，则没有违反性质4，退出循环

• 如果z1.p是红色，由于z1和z1.p都为红色，则违反性质4

  那么性质2和性质4，最多只有一个性质被破坏。

Case2：z的叔节点y是黑色的且z是一个右孩子

Case3：z的叔节点y是黑色的且z是一个左孩子

对于case2和case3中，z的叔父节点y是黑色的，通过z是z.p的右孩子还是左孩子来区别这两种情况。

对于case2，z是一个z.p的右孩子，对于case2的第一行代码，就是z=z.p，即使将z往上移了一层，然后通过对z进行左旋又将z下移了一层，所以此时z变成了左孩子，z.p.p的身份保持不变。这样操作就把case2活生生变成了case3了。

对于case3，改变某些节点的颜色并做一次右旋，以保持性质5，这样在一行中干部在有两个红色节点，所有的处理到此完毕。

case2,case3参考下图：可以参照《算法导论》p182 13-6

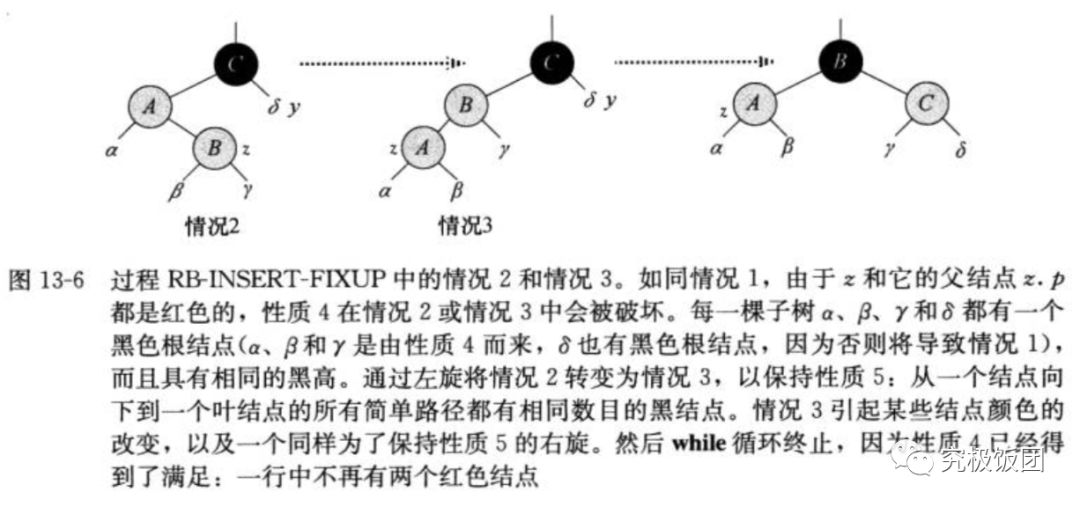
我们来看下case2和case3是否保持了循环不变式

a：case2让z指向了z.p,z还是红色。在case3中z的颜色都没有改变，还是红色

b：case2，case3，z.p都还是红色

c：由于节点z在case2和case3中都不是根节点，所以性质2没被破坏。又由于唯一着为红色的节点在case3中通过右旋成为一个黑色节点的子节点，性质2也没有被违反。case2和case3修正了性质4的违反，也不会引起对其他红黑性质的违反。所以最多一个性质被破坏，也成立。最终通过了case3之后退出循环。

删除

讲完了红黑树的性质和红黑树的插入，最后来讲下红黑树的删除，删除操作相比于插入要稍微复杂点。

在了解红黑树节点之前，要先知道其中两个子过程，

• 一个是RB-TRANSPLANT：子树替换

• 一个是TREE-MINIMUM：查找一个子树的最小节点

RB-TRANSPLANT

在删除红黑树节点的时候，会经常用到一个子过程RB-TRANSPLANT,这个过程是借鉴了二叉搜索树中的TRANSPLANT子过程，意思是一样的，这个操作就是把一个子树替换另外一个子树并成为其u父节点的的孩子节点。

看看RB-TRANSPLANT伪代码

RB-TRANSPLANT(T,u,v){                 // 在T树中，把v子树替换掉u子树
    if u.p == T.nil
        T.root = v
    elseif u == u.p.left
        u.p.left = v
    else u.p.right = v
    v.p = u.p                        // 删除u之后，节点u的父节点变成了v的父节点
}

TREE-MINIMUM

查找最小节点这个方法简单，一看伪代码就知道，如果要寻找z的后继要寻找z的右子树的最小的节点，即：TREE-MINIMUM(z.right)

TREE-MINIMUM(x){
    while x.right != T.nil 
        x = x.right
} 

删除过程

了解完RB-TRANSPLANT子过程之后，我们可以正式的来看下删除过程RB-DELETE

第一步实现：RB-DELETE(T,z)

看看RB-DELETE伪代码

RB-DELETE(T,z){
1    y = z                                    
2    y-original-color = y.color
3    if z.left = T.nil {                         // 如果z的左子树为哨兵，则直接把z的右子树替换z
4        x = z.right                            
5        RB-TRANSPLANT(T,z,z.right)
6    } elseif z.right == T.nil {                    // 如果z的右子树为哨兵，则直接把z的左子树替换z
7        x = z.left                             
8        RB-TRANSPLANT(T,z,z.left)
9    } else {                                   // 如果z有两个节点，则寻找z的后继节点
10        y = TREE-MINIMUM(z.right)
11        y-original-color = y.color
12        x = y.right
12        if y.p == z {
14            x.p = y
15        } else {
16            RB-TRANSPLANT(T,y,y.right)
17            y.right = z.right
18            y.right.p = y
19        }
20        RB-TRANSPLANT(T,z,y)
21        y.left = z.left
22        y.left.p = y
23        y.color = z.color
24    }
25    if y-original-color = BLACK
26        RB-DELETE-FIXUP(T,x)
}

在上面的代码中，可以看出

始终维持节点y要不是从树中移除的节点，要不是移动到树内替换节点z的节点。

RB-DELETE过程参考下图：可以参照《算法导论》p167 12-4

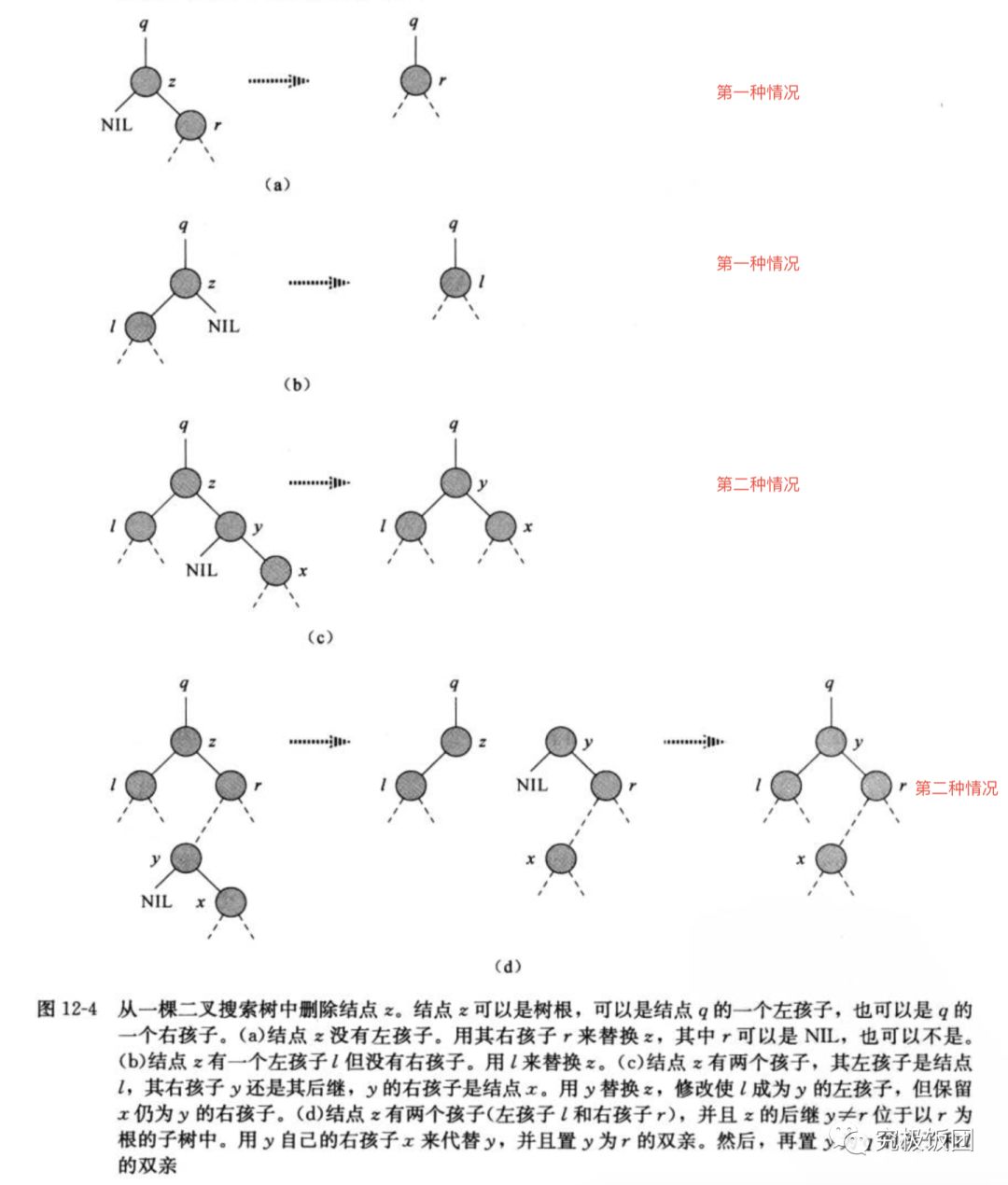
• 第一种情况：当z的子节点少于2个时，第1行y指向z，并通过把z的左孩子或者是右孩子替换掉z，来移除z，并且y-originnal-color代表的是要被移除节点的颜色，z的颜色要随着z的删除会在树中被消除。如果y-originnal-color是黑色，就有可能会引起红黑树性质的改变，则修复红黑树时，修复的就是x（z的左孩子或者右孩子）对红黑树影响。

• 第二种情况：当z有两个子节点时，第10行将y指向了z的后继节点，y将移至到z的位置，y-originnal-color代表的是z的后继节点y的颜色，因为在第16行，y的右子树要替换掉y节点，而之后替换z的节点重新被设置成了z的颜色。所以此时z的后继节点的颜色会被消除。如果y-originnal-color是黑色，就有可能会引起红黑树性质的改变，则修复红黑树时，修复的就是x（z的后继节点的右孩子）对红黑树影响。

第二步实现：RB-DELETE-FIXUP(T,x)

如果y-originnal-color是黑色，则会产生三个问题，就需要通过RB-DELETE-FIXUP方法对红黑树进行补救,

第一个问题:在第一种情况下，z或者y是红黑树的根节点，那么z或者y的一个红孩子成为了新的节点时，就违反了性质2。

第二个问题:在第二种情况下，x和x.p都是红色，则违反了性质4。

第三个问题:在第二种情况下，用x覆盖掉了y（z的后继节点），并移动y到了z的节点上，之后y的颜色被着了z的颜色，将会导致先前包含y的任何简单路径上黑色节点的个数少1，这将会违反性质5，因此y的任何祖先都不满足性质5。

关于第三个问题的解决思路：将占有y原来位置上的节点x视为还有一重额外的黑色。也就是说，如果将现在的包含x的路径上黑节点树加1，在这种假设下性质5才会成立。当将黑节点y删除或者移动时，将其黑色下推给节点x，节点额外的黑色是针对x节点的，而不是反映在它的color属性上。

• 如果x是红色的，就把x当做是红黑色的。

• 如果x是黑色的，就把x当成双重黑色的。

了解了因为y-originnal-color是黑色导致的三个问题之后，我们先来看看伪代码，我们看看是如何解决这三个问题的。

RB-DELETE-FIXUP(T,x) {
1 while x != T.root and x.color == BLACK {
2    if x == x.p.left {
3        w = x.p.right                                       // w为x的兄弟节点
4        if w.color == RED                                       
5            w.color = BLACK                                 // case1    
6            x.p.color = RED                                 // case1    
7            LEFT-ROTATE(T,x,p)                              // case1    
8            w = x.p.right                                   // case1    
9        elseif w.left.color == BLACK and w.right.color = BLACK
10            w.color = RED                                  // case2 
11            x = x.p                                        // case2 
12        elseif w.right.color = BLACK
13            w.left.color = BLACK                           // case3 
14            w.color = RED                                  // case3 
15            RIGHT-ROTATE(T,w)                              // case3 
16            w = x.p.right                                  // case3 
17        else w.color = x.p.color                           // case4
18            x.p.color = BLACK                              // case4
19            w.right.color = BLACK                          // case4
20            LEFT-ROTATE(T,x.p)                             // case4
21            x = T.root
22    } else (same as then clause with "right" and "left" exchanged)
   }
23 x.color = BLACK
}

在循环中，x总是指向一个双重黑色的非根节点。while循环中的目标就是将额外的黑色沿着树上移，通过执行适当的旋转和重新着色，直到：

1. x指向红黑节点，退出循环，并在第23行，将x节点设置为（单个）黑色。

2. x指向根节点，退出循环，并在第23行，简单地移除额外的颜色，将x节点设置为（单个）黑色。

接着需要考虑到在循环体内有8种情况，而其中4种与另外4种是对称的。这取决于x是其父节点x.p的左孩子还是右孩子，伪代码是给出了x是左孩子的代码，

注意：代码中w为x的兄弟节点，并且由于x是双重黑色的，所以w不可能是T.nil，否则x.p到x的黑节点个数会大于x.p到w的黑节点个数。

下面来讲解下以x是x.p的左孩子为例的四种情况：

• Case1：x的兄弟节点w是红色的

• Case2：x的兄弟节点w是黑色的，而且w的两个子节点都是黑色的

• Case3：x的兄弟节点w是黑色的，而且w的左孩子是红色的，右孩子是黑色的

• Case4：x的兄弟节点w是黑色的，而且w的右孩子是红色的

RB-DELETE-FIXUP过程参考下图：可以参照《算法导论》p186 13-7

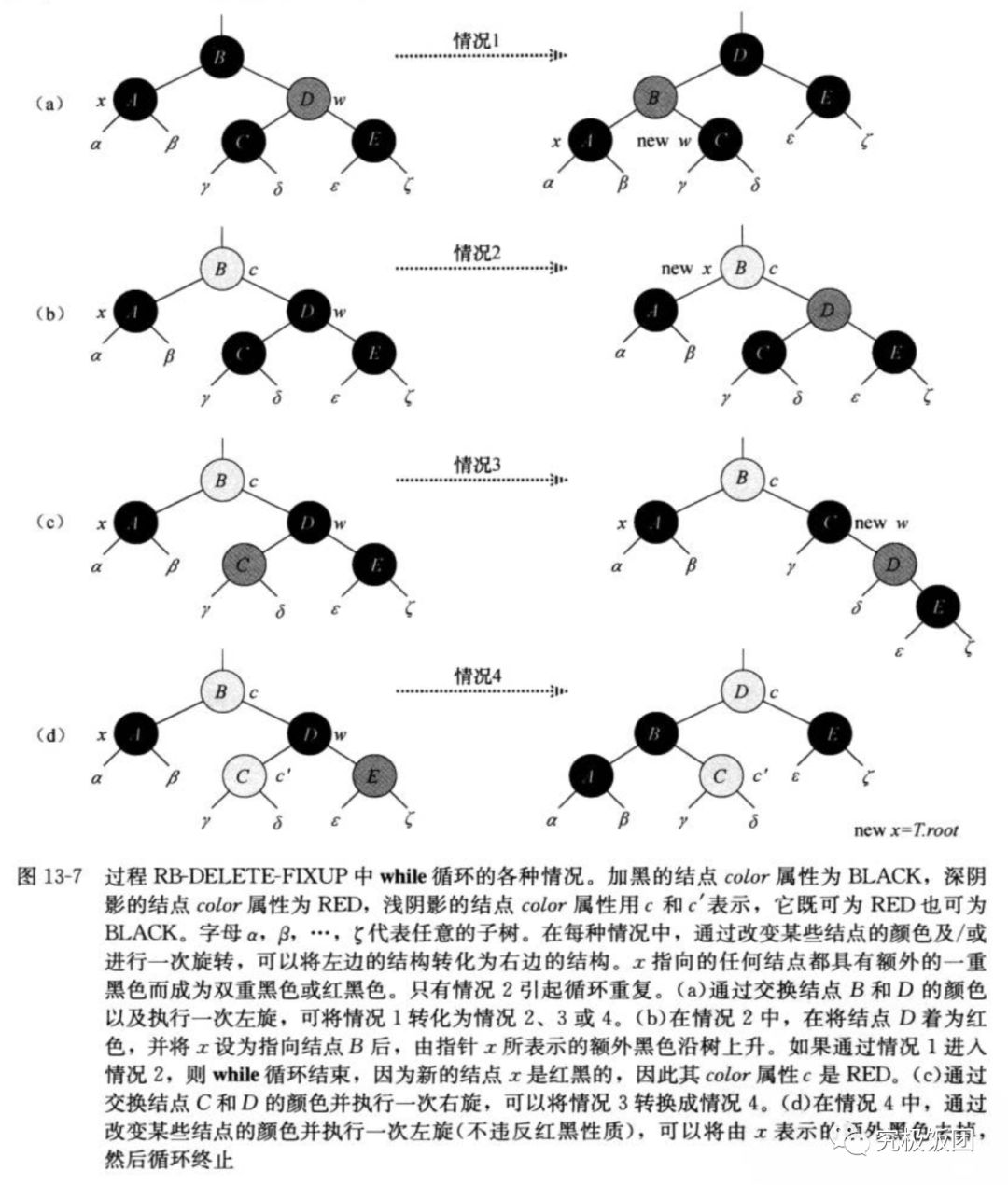
Case1：x的兄弟节点w是红色的

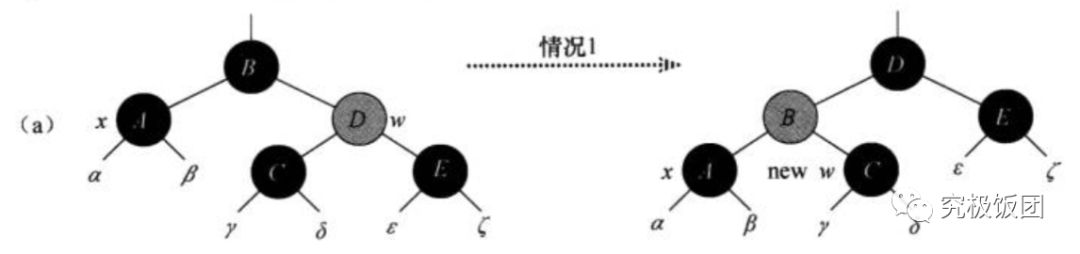
要解决问题，必须要把case1转换成case2，case3，或者case4进行处理，所以w必须要成为黑色。因为w是红色节点，所以w的父节点x.p肯定是黑色的。所以把w和x.p的颜色进行交换，并对x.p进行一次左旋，w被重新赋值成x的新的兄弟节点，这样子变换之后，就不会违反红黑树的任何性质。这个可以通过看图进行理解。

case2：x的兄弟节点w是黑色的，而且w的两个子节点都是黑色的

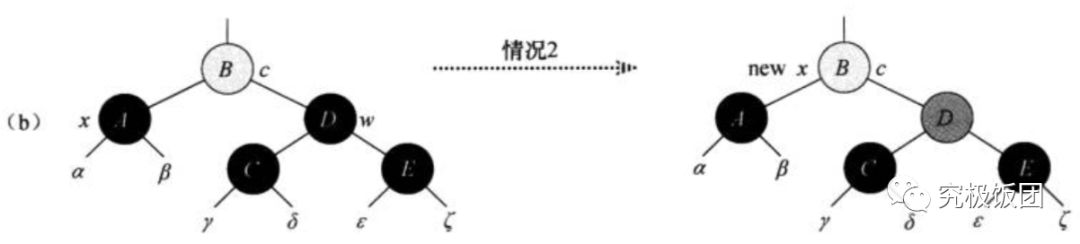
这种情况是最好理解的，因为w和w的两个子节点都是黑色，所以就把x和w上去掉一重黑色，使得x是有一重黑色，而w为红色。为了补偿从x和w中去掉的一重黑色，在原来可能是红色也可能是黑色的x.p上新增一重额外的黑色。通过将x.p作为新节点x来继续while循环。所以新节点x，也可能是红黑色，或者是双重黑色。

• 当新节点是红黑色时，就可以退出循环，然后再对新节点x着一重黑色。

• 如果是双重黑色，得要继续进行执行循环。

注意：如果是通过case1进入case2的话，则这个时候case2中原来的x.p是红色的，则新节点x是红黑色的。因此新节点x的color是RED的，在测试循环条件后会终止循环。然后将新节点设置为（单一）黑色

case3：x的兄弟节点w是黑色的，而且w的左孩子是红色的，右孩子是黑色的

如果碰到case3，我们需要把case3转化case4。我们可以交换w和其左孩子w.left的颜色，然后对w进行右旋，这样子不会违反红黑树的任何性质。现在x的新兄弟节点w是一个有红色右孩子的黑色节点，这样子我们就把case3转为了case4。

case4：x的兄弟节点w是黑色的，而且w的右孩子是红色的

通过第17，18，19行的

w.color = x.p.color    
x.p.color = BLACK        
w.right.color = BLACK

对某些节点颜色改变之后，并对x.p做一次左旋之后，就去掉了x的额外黑色，从而使得它变成单重黑色，而且不会破坏红黑树的任何性质。然后将x设置为根T.root后，循环终止。

时间复杂度

RB-INSERT的时间复杂度

由于一颗有n个节点的红黑树的高度为O(lgn),所以除去RB-INSERT-FIXUP的运行时间之外RB-INSERT要花费O(lgn)。在RB-INSERT-FIXUP中仅仅当case1发生，指针z才会沿着树上升2层，while循环才会重复执行，执行了case2或者case3，while循环就结束了。所以while循环可能执行的最多次数为O(lgn),因此RB-INSERT总共花费O(lgn)。

RB-DELETE的时间复杂度

由于一颗有n个节点的红黑树的高度为O(lgn),所以除去RB-DELETE-FIXUP的运行时间之外RB-INSERT要花费O(lgn)。在RB-DELETE-FIXUP中，case1，caes3，和case4在各执行常数次数的颜色改变和至多3次旋转(旋转的时间复杂度为O(1))之后便终止。case2是while循环可以重复执行的唯一情况，然后指针x沿着树上升至多O(lgn)次,并且不执行任何旋转。所以RB-DELETE-FIXUP要花费O(lgn)，做至多3次旋转，因此RB-DELETE总共花费O(lgn)。