AVL平衡二叉树，红黑树原理

Posted 2021-04-04 HelloWorld搬运工

二叉搜索树

插入和删除操作必须先查找，查找效率代表了二叉搜索树中各个操作的性能

最优情况：二叉搜索树为完全二叉树，比较次数Log2^N

最坏情况：二叉搜索树为单支树，平均比较次数N/2

平衡二叉树

平衡树： AVL树，红黑树

AVL树：（二叉搜索树改良版）

AVL树条件：具有二叉搜索树的性质，其左右子树高度之差绝对值不超过1

若AVL树，有N个节点，高度为OlogN，平均搜索时间复杂度O(logN)

旋转

每一次的插入数值之后，树的平衡性可能被破坏，需要通过旋转来保持平衡性

插入节点时候分四种情况，对应下面四种旋转方法

 插入方式       描述                         旋转方式

 LL 在a左子树根节点的左子树上插入节点而破坏平衡    右旋

 RR 在a右子树根节点的右子树上插入节点而破坏平衡    左旋

 LR 在a左子树根节点的右子树上插入节点而破坏平衡  左右双旋

 RL 在a右子树根节点的左子树上插入节点而破坏平衡 右左双旋

红黑树：（二叉搜索树改良版）

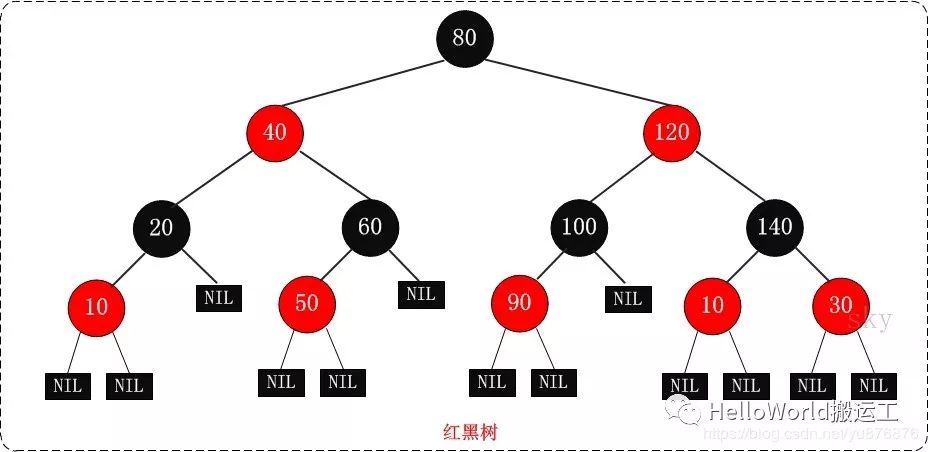
红黑树特性：

1 每个节点只有两种颜色黑色或红色

2 根节点是黑色

3 叶子节点是黑色（叶子节点：指的的空节点）

4 如果一个节点是红色，则它的子节点必须是黑色

5 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点

总结：2，5特性确保了没有一条路径会比其他路径长出两倍，

因此红黑树是相对接近平衡的二叉树！！！！！

红黑树的应用

主要用来存储有序的数据，时间复杂度OlogN，效率非常高

例如：C++ STL中的set,map，以及Linux虚拟内存管理，应用红黑树实现

红黑树的基本操作-旋转

红黑树基本操作是添加，删除，但是操作后会破坏红黑树的性质，需要进行旋转保持红黑树的特性

左旋：

左旋 ： （意味着被旋转的节点将变成一个左节点）

将Y的左孩子B设为X的右孩子

将X设为Y左孩子的父节点

将X的父节点指设为Y的父节点

右旋

右旋：（意味被旋转的节点将变成一个右节点）

将X的右孩子设为Y的左孩子

将Y设为X右孩子的父亲

将Y的父亲设置为X的父亲

红黑树的基本操作—添加

第一步：将红黑树当作一颗二叉搜索树，将节点插入

找到合适的位置进行插入，插入后需要进行旋转调整和着色操作

第二步：将插入的节点着色为“红色”

将插入节点着色为红色不会违背特性5，即需要处理的情况就相对越少

第三步：通过一系列的旋转或者着色操作，重新成为一颗红黑树

有可能违背特性(4)： 如果一个节点是红色的，则它的子节点必须是黑色的。

添加操作：

新建节点Y，将Y设为空节点

设红黑树T的根节点为X

找出要插入的节点Z，在二叉树T中的位置Y

设置Z的父亲为Y

情况1：若Y是空节点，则将Z设为根

情况2：若Z所包含的值<Y所包含的值，则将Z设为Y的左孩子

情况3：若Z所包含的值>Y所包含的值，则将Z设为Y的右孩子

Z的左孩子设为空，Z的右孩子设为空

对红黑树的节点进行颜色修饰和旋转