2-3查找树To红黑树---红黑树基础

Posted 2021-04-04 后端开发与算法

2-3查找树

为了保证查找树的平衡树，我们需要一些灵活性，因此在这里我们允许树中的一个结点保存多个键。上一篇主要学习了2-3-4树的基本原理和实现，2-3树和2-3-4树的区别就是后者允许存在4-节点（三个键4条链接），而2-3树只允许2-（一个键2条链接）结点和3-（二个键3条链接）结点，2-和3-结点中的每条链接都对应着其中保存键所分割产生的区间。

一颗完美平衡的2-3查找树的所有空连接到根节点的距离都应该是相同的。简洁起见，这里我们用2-3树指代一颗完美平衡的2-3查找树。

查找

将二叉查找树的查找算法一般化我们就能够直接得到2-3树的查找算法。要判断一个键是否在树中，我们先将它与根节点比较，如果它和其他任意一个相等，查找命中，否则我们就根据比较的结果找到相应的区间链接，并在指向其子树中递归地继续查找。如果最后这个是个空链接，那么未找到。

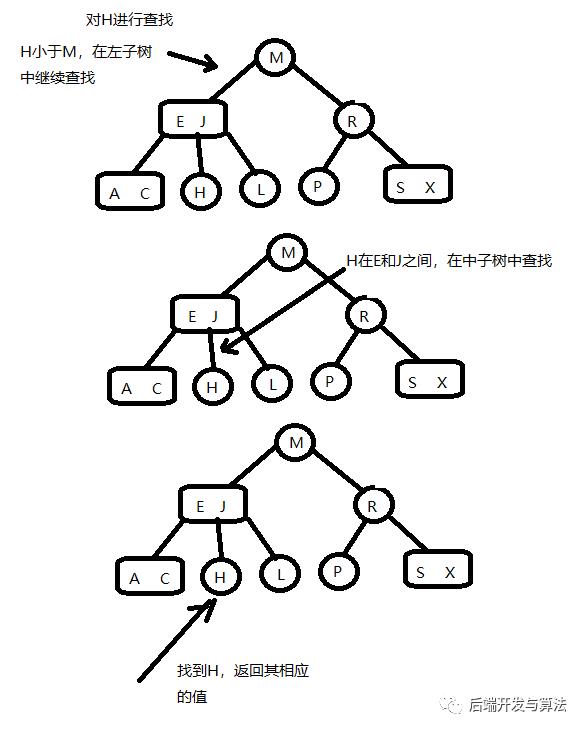
向2-结点插入新键

要在2-3树中插入一个新的结点，我们可以和二叉查找树一样先进行未命中查找，然后把新结点挂在树的底部，但是这个的话树无法保证完美平衡性。我们使用2-3树的主要原因是它能在插入后继续保持平衡。如果未命中查找结束于一个2-结点，那么我们就将这个2-结点替换为一个3-结点，将要插入的值保存在其中即可。

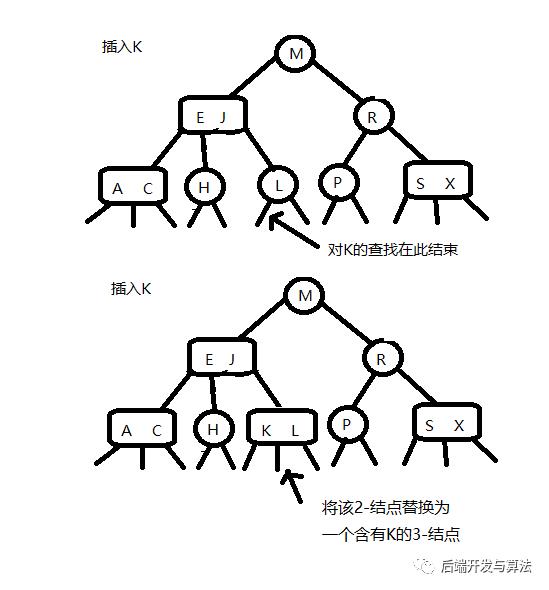
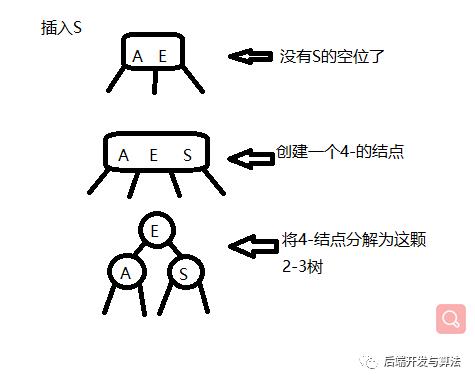
向一颗含有一个3-结点的树中插入一个新键

这棵树中有两个键，所以在它唯一的结点中已经没有可以插入新建的结点空间了。为了将新键插入，我们先临时将新键存入该结点中使之成为一个4-结点，它很自然地扩展了以前的结点并包含3个键和4条链接，创建一个4-结点很方便，因为它很容易将它转化为一颗由3个2-结点组成的2-3树，其中一个结点（根）含有中键，一个结点含有3个键中的最小者（和根节点左链接相连），一个结点含有3个键中的最大者（和根节点右链接相连）。这棵树既是一颗含有3个结点的二叉查找树，同时也是一颗完美平衡的2-3树，其中所有的空链接到根节点的距离都相等。插入之前高度是0，插入之后树的高度为1.【此处分解和2-3-4树的满节点为根节点分裂原理一样】

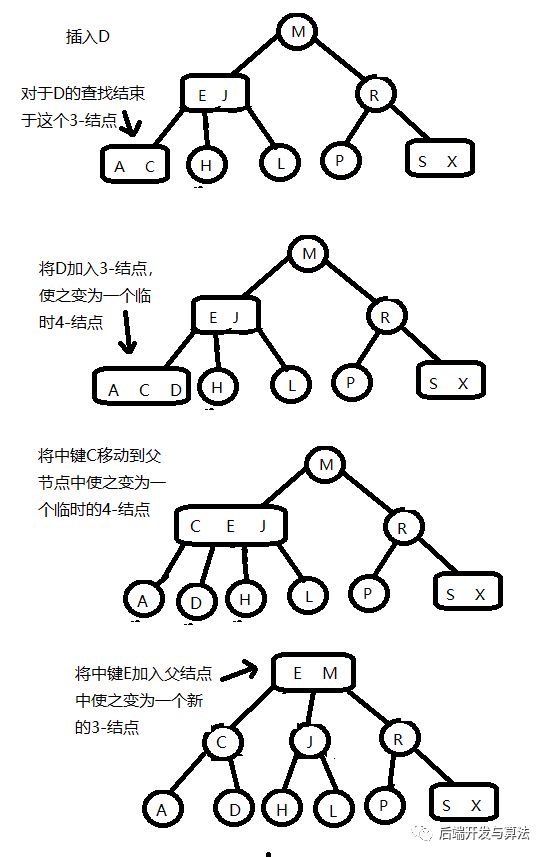
向一个父节点为2-结点的3-结点中插入新键【核心】

假设未命中查找结束于3-结点，且它的父节点为2-结点。在这种情况下，我们需要在维持树的完美平衡下为新键腾出空间。我们像刚刚一样构造一个临时4-结点将其分解，但此时我们不会为中键创建一个新的结点，而是将其移动到原来的父节点中。可以看做这次转化为指向原3-结点的一条链接替换为新父节点中的原中键左右两边的两条链接，分别指向新的两个2-结点。根据我们的假设，父节点中是有空间的：父节点是一个2-结点（一个键两条链接），插入之后变为了一个3-结点（两个键3条链接）。另外，此次变换也不会影响2-3树的完美平衡性，树仍然是有序的，因为中键被移动到父节点中去了，树仍然是完美平衡的，插入后所有的空链接到根节点的距离仍然相同。【此处分解和2-3-4树的满节点不为根节点分裂原理一样】

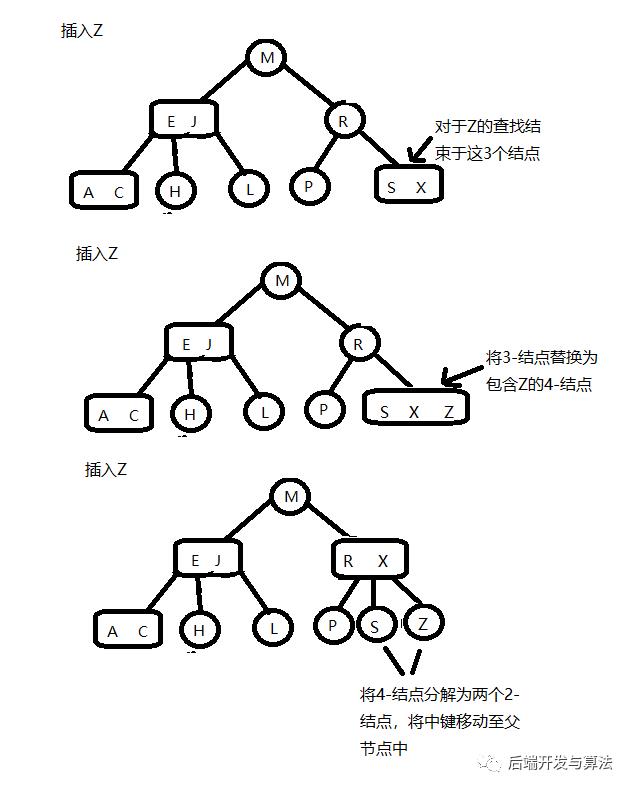
向一个父节点为3-结点的3-结点中插入新键

现在假设未命中结点的查找结束于一个父节点为3-结点的结点。我们再次和刚才一样构造一个临时的4-结点并分解它，然后从它的中键插入它的父节点中。但是父节点也是3-结点，因此我们在使用这个中键构造一个新的临时结点4-结点，然后在这个结点上进行相同的变换，即分解这个父节点并将它的中键插入到更高层的父节点中，直至遇得到一个2-结点并将它替换为一个不需要继续分解的3-结点，或者是到达3-结点的根。

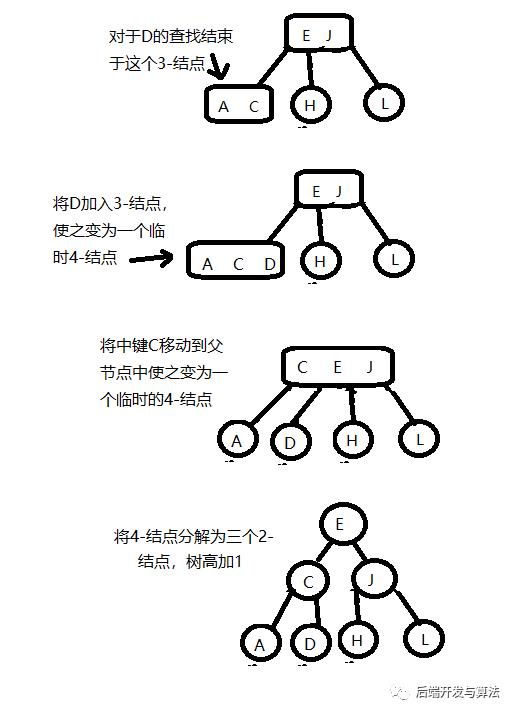
分解根节点

如果从插入结点到根节点对的路径上全是3-结点，我们的根节点最终会变为一个4-结点。此时我们可以按照向一颗只有3-结点的树中插入新键的方法处理这个问题。我们将临时的4-结点分解为3个2-结点，使树的高度加1。这次变换仍然保持了树的完美平衡性。

局部变换

讲一个4-结点分解为一颗2-3树可能有6中情况，都总结在了下面。这个4-结点可能是根节点，可能是一个2-结点的左子节点或者右子节点，也可能是一个3-结点的左子节点、中子节点或右子节点。2-3树插入算法的根本在于这些变换是局部的：除了相关的结点和链接之外不必修改检查树的其他部分。每次变换中，变更的链接数量不会超过一个很小的常数。需要特别之处的是，不光在树的底部，树的任何地方都要符合相应的模式，变换都可以执行。每个变换都会将4-结点中的一个键送入它的父结点中，并重构相应的链接而不必涉及树的其他部分。

全局性质

这些局部变换不会影响树的全局有序性和平衡性：任意空链接到根节点的路径长度大都是相等的。

思路转变

    至此已经弄明白了2-3树的所有变换，虽然我们可以用不同的数据类型表示2-结点和3-结点并写出变换所需的代码，但是这种直白的表示方法实现大多数的操作并不方便，因为需要处理的情况实在太多。我们需要维护两种不同类型的结点，将被查找的键和结点中的每个键进行比较，将链接和其他信息从一种结点复制到另一种结点，将结点从一种数据类型转换到另外一种类型等。实现这些不仅需要大量代码，而且它们所产生的额外开销可能会使算法比标准二叉树更慢。

红黑查找树

    上文讲的2-3树插入算法并不难理解，但是所需要的消耗和代码处理太多，我们这里使用一种名为红黑二叉树的简单数据结构来表达并实现它。

    红黑二叉查找树的背后思想就是用基本的标准二叉查找树（完全由2-结点构成）和一些额外的信息（替换3-结点）来表示2-3树。

    我们将树中的链接分为两种类型：红链接将2个2-结点连接起来构成一个3-结点，黑链接则为2-3树中的普通链接。我们将这种方式表示的2-3树的二叉查找树称为红黑二叉查找树（以下简称红黑树）。

定义

    红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树：

1. 红链接均为左链接

2. 没有任何一个结点同时和两条红链接相连；

3. 该树是完全黑色平衡的，即任何空链接到根节点的路径上黑链接的数量相同

一一对应

    如果我们将一颗红黑树中的红链接画平，那么所有的空链接到根节点的距离都是相同的，如果我们将由红链接相连的结点合并，那么我们就的得到了一颗2-3树。

    红黑树章节未完待续...