二叉树与红黑树

Posted 2021-04-04 记录世界 from antonio

红黑树在工程中的使用，红黑树是平衡树的一种。

1. 红黑树顺序的功能

2. 快速查找的功能

1.二叉树插入

1. 如果比当前根节点大，就插到右子树

2. 如果比当前根节点小，就插到左子树

3. 再与根节点的子树去比较，决定插入到左子树，还是右子树。

一直到左右子树为空的情况。注意：二叉树的插入，只能作为叶子节点。

代码中的tmp指向的是node的父节点。下图的根节点是tmp指向的，node是指向根节点的子节点。

//二叉树创建节点，一般是不对外开放struct bstree_node *bstree_create_node(KEY_VALUE key){
 struct bstree_node *node = (struct bstree_node *)malloc(sizeof(struct bstree_node)); if(node == null) return null;
 node->data = key; node->bst.left = node->bst.right = null; return node;}
//二叉树插入int bstree_insert(struct bstree *T,KEY_VALUE key){ if(T == null) return -1; //如果根节点为空，就创建一个树 if(T->root == NULL) { T->root = bstree_create_node(key); return 0; }
 //接替根节点 //指向父节点的子节点 struct bstree_node *node = T->root; //指向父节点 struct bstree_node *tmp = T->root;
 //把一个值插入到相应的位置 //这个while循环就相当于，一个查找的过程 while(node != NULL) { //第一次，父节点和子节点指向的同一个位置 tmp = node; //如果要插入的值，小于当前节点的值，插入左子树 if(key < node->data) { node = node->bst.left; }else if(key > node->data){
 //如果要插入的值，大于当前节点的值，插入右子树 node = node->bst.right; }else{
 //如果相同节点，不插入，直接返回，提示有个相同节点 printf("exit!!!
"); return -2; }
 }
 //当这个循环走完,终于找到要插入的位置 if(key < tmp->data) { //插入左边的叶子节点 tmp->bst.left = bstree_create_node(key); }else{ //插入右边的叶子节点 tmp->bst.rignt = bstree_create_node(key); }
 return 0;}
//二叉树traversal:遍历//如果不用递归实现遍历，就需要借助栈的方式int bstree_traversal(struct bstree_node *node){
 if(node == null) return 0; //左中右，中序遍历 bstree_traversal(node->bst.left); printf("%4d",node->data); bstree_traversal(node->bst.right);
}
//二叉树的测试和遍历的代码int main() {
 int keyArray[ARRAY_LENGTH] = {24,25,13,35,23, 26,67,47,38,98, 20,13,17,49,12, 21,9,18,14,15};
 struct bstree T = {0}; int i = 0; for (i = 0;i < ARRAY_LENGTH;i ++) { bstree_insert(&T, keyArray[i]); }
 bstree_traversal(T.root);
 printf("
");}

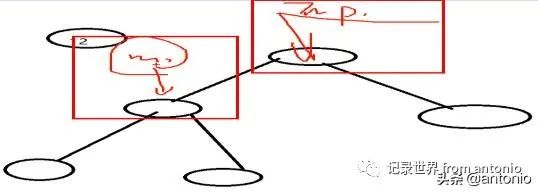
tmp指针，node指针，一直在往下移动。为什么这样呢？因为二叉树没有回溯，没有办法返回上一层，找不到父节点。所以这里必须用两个指针。

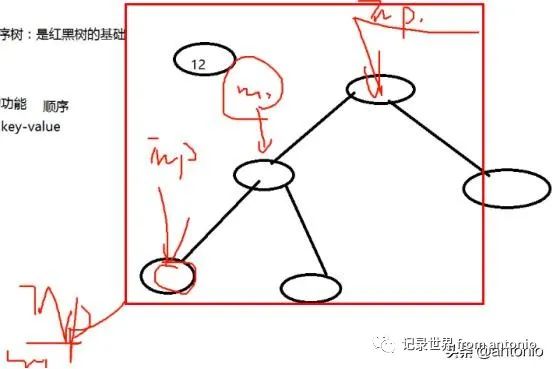
当代码中的循环走完的时候,node指向空。

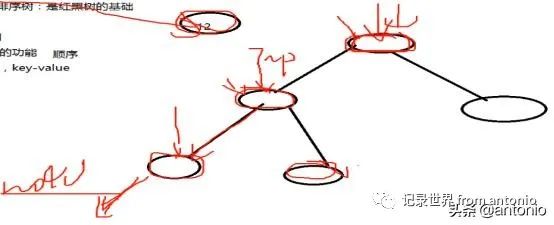
//遍历二叉树

由于遍历的流程都是一样，都可以采用递归的步骤。

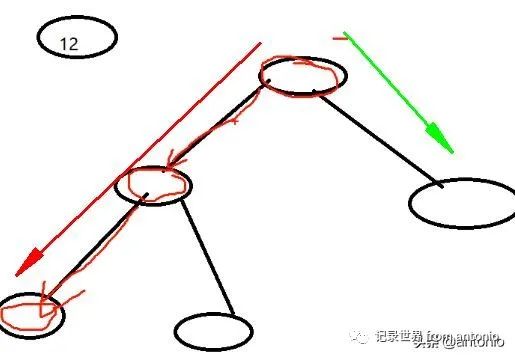
经过这个节点有3次，第一次经过这个节点是根左右，也就是前序遍历。第二次经过这个节点是左根右，也就是中序遍历。第三次经过这个这个节点是左右根，也就是后序遍历。

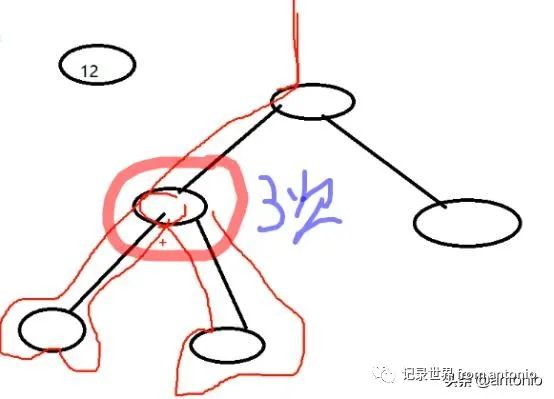
经过这个节点有3次，第一次经过这个节点是根左右，也就是前序遍历，分别打印23、15、7。第二次经过这个节点是左根右，分别打印7、15、18，也就是中序遍历。第三次经过这个这个节点是左右根，也就是后序遍历，分别打印18、28、23。

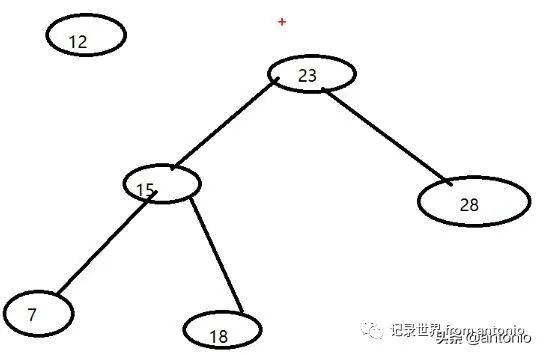
二叉树的删除

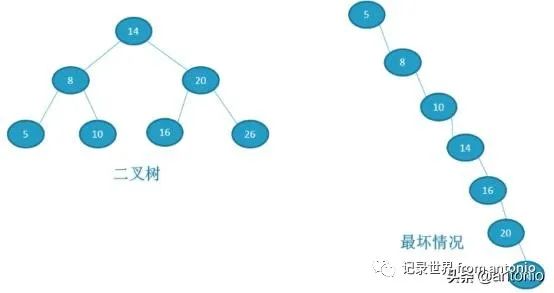
删除就是先查找的这个节点，然后把子树接上去。二叉树，最多两个分两个叉。最坏的情况就是类似链表的情况。

2.红黑树

红黑树性质:

第2，3点表示，黑色节点可以是相邻的关系。

第4点表示，红色的节点，不能是相邻关系。

第5点表示，这个是一个平衡的关系，平衡的是黑色节点的高度，与红色节点没有关系，也就是说红色节点是打酱油的。

那红色节点的作用是什么呢？

主要是用来区分不同的情况。比如做旋转。

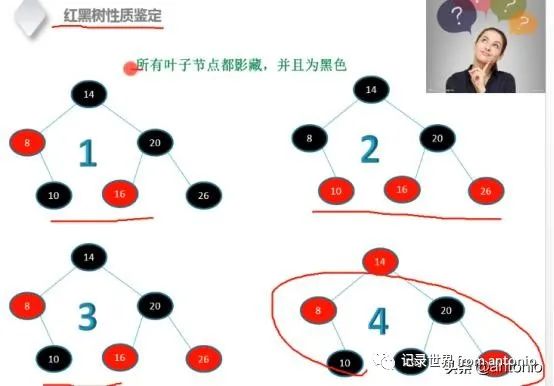
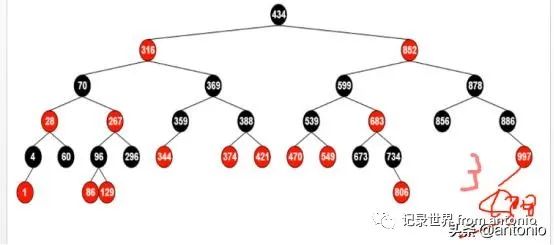
第一个不满足第5种情况，根节点左子树黑色的高度是2，而右子树，左边的高度是3。

第二个满足条件，是红黑树。

第三个不满足第5种情况，就是黑高不一致。

第四个也不满足第一个情况，根节点必须是黑色。

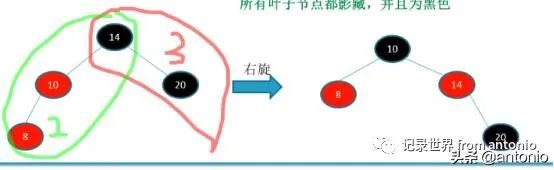
所有叶子节点影藏，并且默认是黑色。计算高度，也要把隐藏的算进去。

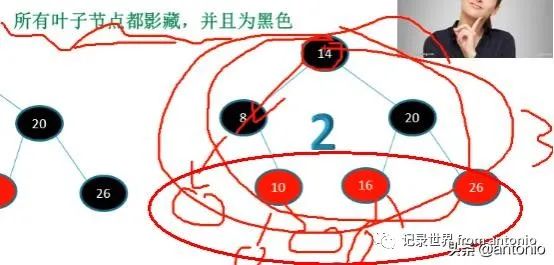
第二个是满足条件的，第二个是红黑树。

树的旋转

1.左旋

如果把当做父节点，然后左旋，则x会被当做y的左子树，b的位置也要发生改变。所以每个旋转的节点，都有3个方向，这三个方向都要发生改变，但是这三个方向都有个parrent节点，实际就是双重方向的，那总共就要改变6根指针。

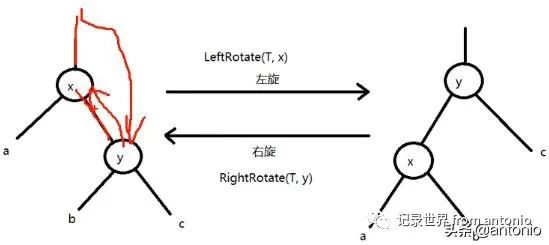
//旋转是红黑树的基础

那6个方向呢？

第一个是指向x的指针

第二个是指向Y的指针

第三个是x指向y的指针

第四个是y指向x的指针

第五个是y指向b的指针

第六个是x指向b的指针

//旋转是红黑树的基础//为了判断叶子节点隐藏的都是黑色，那需要把整个红黑树都传进来//以当前节点为轴心，这个当前节点是可以找到//这个是左旋的函数void rbtree_left_rotate(rbtree *T,rbtree_node *x){ //y等于x的右子树 rbtree_node *y = x->right;
 //1方向.现在x的右子树指向原来y的左子树 x->right = y->left; //如果y的左子树不是影藏节点 if(y->left != T->nil) { //2方向.原来y的左子树的父节点指向x y->left->parrent = x; }
 //这里旋转的时候，x是根节点,旋转完成后，y变为根节点
 //3方向.现在y的parrent指向原来x的parrent y->parrent = x->parrent;
 //4方向.如果x的父节点是叶子节点，是空，代表x是root节点。 if(x->parrent == T->nil) { //那根节点指向y T->root = y;
 }else if(x == x->parrent->left) { //如果x是父节点的左子树,那么就把原来x父节点的左子树，指向y x->parrent->left = y;
 }else { //这种情况就把原来x父节点的右子树，指向y x->parrent->right = y;
 }
 //5方向.现在y的左子树指向了x y->left = x; //6方向.现在x的父节点指向了y x->parrent = y;}
//x--y:需要换//y-->x:需要换//left-->right:需要换//right-->left:需要换
void rbtree_right_rotate(rbtree *T,rbtree_node *y){ //y等于x的右子树 rbtree_node *x = y->left;
 //1方向.现在x的右子树指向原来y的左子树 y->left = x->right; //如果y的左子树不是影藏节点 if(x->right != T->nil) { //2方向.原来y的左子树的父节点指向x x->right->parrent = y; }
 //这里旋转的时候，x是根节点,旋转完成后，y变为根节点
 //3方向.现在y的parrent指向原来x的parrent x->parrent = y->parrent;
 //4方向.如果x的父节点是叶子节点，是空，代表x是root节点。 if(y->parrent == T->nil) { //那根节点指向y T->root = x;
 }else if(y == y->parrent->right) { //如果x是父节点的左子树,那么就把原来x父节点的左子树，指向y y->parrent->right= x;
 }else { //这种情况就把原来x父节点的右子树，指向y y->parrent->left= x;
 }
 //5方向.现在y的左子树指向了x x->right= y; //6方向.现在x的父节点指向了y y->parrent = x;}

旋转后的解释就是，原来指向x的，现在指向了y。原来x指向左子树的，现在指向了x。x指向了Y的左子树。其它就是把parrent节点指向。

左旋不是原来的左右关系发生变化。不管是左右旋，红黑树的颜色都不会发生变化，旋转前需要判断颜色变化。旋转是为了寻求平衡。寻求平衡的目的是追求黑高的平衡，当黑高的高度不一致时，通过黑高来达到左右子树一致。

右旋，就是把原来的x换成y，y换成x。

//红黑树的插入与二叉树的插入是一样的性质，红黑树的插入也是插到最底下的叶子节点。

插入不会引起左右旋和其它改变。插入完成之后，会引起一个调整。

红黑树插入新节点之前，这个树已经是红黑树了。

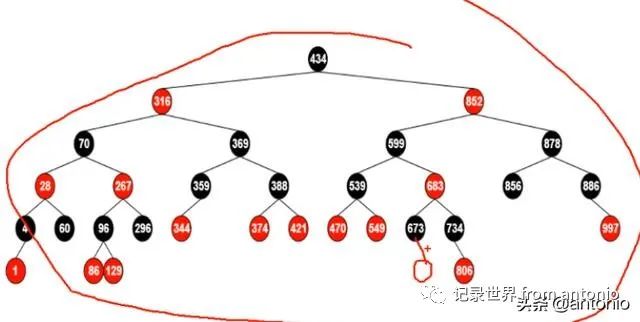
插入节点

新插入的节点最好是红色，因为不影响黑高。如果新插入节点的父节点是红色，那么就需要调整二叉树，为什么？因为红色节点的子节点必须是黑色，这样也会影响黑高。

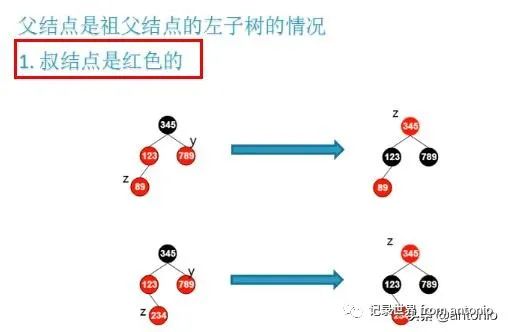
当前节点是红色，z的父节点是红色，z的祖父节点肯定是黑色的。叔父节点是可能是红色，可能是黑色

这里就存在3种情况：

第一种情况是插入的必须是红色节点(这也是确定的)，叔父节点是红色的,这个条件是确定的。

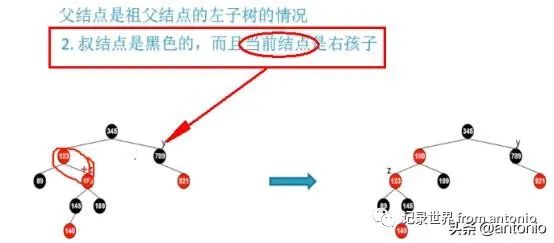
第二种情况是插入的必须是红色节点(这也是确定的)，叔父节点是黑色的。这个时候需要对祖父节点进行左旋。

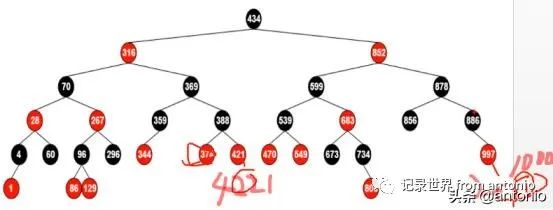
第三种情况是插入一个900

//父节点为红色，就需要调整红黑树，否则会影响黑高void rbtree_insert_fixup(rbtree * T,rbtree_node * z){
 while(z->parrent->color == RED) { //如果父节点是祖父节点的左子树 if(z->parrent == z->parrent->parrent->left) {  //获取叔父节点 rbtree_node *y = z->parrent->parrent->right; //如果叔父节点是红色 //这里有2种情况 if(y->color == RED) { //把父节点颜色变为黑色 z->parrent->color = BLACK; //当前节点也变为黑色 y->color = BLACK; //祖父节点变为红色 z->parrent->parrent->color = RED;
 //再以祖父节点为旋转即可调整黑高 z = z->parrent->parrent;
 }else { //如果叔父节点是黑色,这个时候就需要旋转 if(z == z->parrent->right) { //这个时候,父节点的右子树节点个数多，以父节点进行左旋 z = z->parrent; rbtree_left_rotate(T,z);
 } //定色 z->parrent->color = BLACK; z->parrent->parrent->color = RED; //再进行右旋 rbtree_right_rotate(T, z->parrent->parrent); } }else { //如果父节点是祖父节点的右子树 rbtree_node *y = z->parrent->parrent->left; if(y->color == RED) { //改变作色 z->parrent->color = BLACK; y->color = BLACK; z->parrent->parrent->color = RED; //轴心点 z = z->parrent->parrent;
 }else {
 if(z == z->parrent->left) {
 z = z->parrent; //右旋 rbtree_right_rotate(T,z); } //旋转第二次 z->parrent->color = BLACK; z->parrent->parrent->color = RED; //左旋 rbtree_left_rotate(T,z->parrent->parrent); }
 }
 }
 T->root->color = BLACK;
}
void rbtree_insert(rbtree *T,rbtree_node *z){
 //y是叶子节点 rbtree_node *y = T->nil; //x是根节点 rbtree_node *x = T->root;

 while(x != T->nil) {
 //只要x不是叶子节点 y = x; if(z->key < x->key) { //如果要插入的值小于当前节点的值，那就往当前节点的左子树走 x = x->left; }else if(z->key > x->key) { //如果要插入的值小于当前节点的值，那就往当前节点的右子树走 x = x->right; }else{ //这表示要插入的节点已经存在了 return; }
 }
 //指向节点的末端,把z节点插入进来 z->parrent = y; if(y == T->nil) { //如果y的叶子节点为空 T->root = z; }else if(z->key < y->key) { y->left = z; }else { y->right = z; } //插入节点的左右子树指向空 z->left= T->nil; z->right = T->nil; //插入节点的颜色最好是红色，黑色会影响黑高 z->color = RED;
 //别忘了插入 rbtree_insert_fixup(T,z);

}

红黑树和平衡二叉树区别？

平衡二叉树需要记录树的高度，是一个强平衡二叉树，当左右子树的高度大于1时，这个时候就需要调整。所以平衡二叉树旋转的次数，要比红黑树多。

为什么叔父节点是红色的时候，不需要旋转？

这个时候的黑高是一致的，只需要去改变颜色就行了。

如果叔父节点是黑色的，影响了黑高，那么就需要旋转，如下图。

这里根节点左子树的黑高是2，右子树的黑高是3，出现不一致的情况。就需要调整。

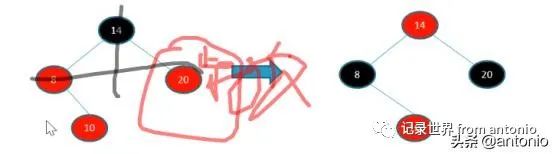
怎样判断是左旋还是右旋？

判断父节点的左子树上节点多，还是右子树节点多，往节点数小的方向去旋转。

如果叔父节点是红色的，那么需要改变颜色即可。

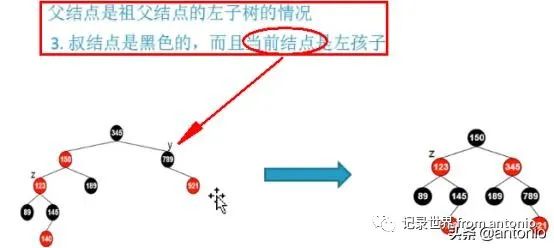
这个时候需要进行2次旋转。当前节点用y表示，第一次旋转在左边，另外一次旋转在右边。

红黑树的删除

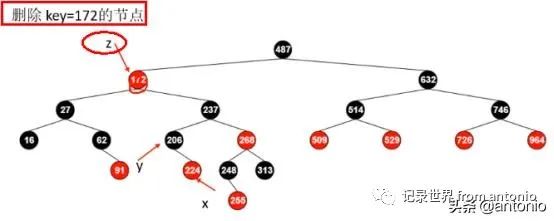
表面是删除172节点，实际上删除节点是172节点的后继，这里找的就是206，也就是y这个节点，那就需要把206(这个是右子树上面的那个最小的点)这个数赋值到z的位置，拷贝到z节点上面去。206被delete后，这个时候206变为237的父节点，如何旋转呢，修复呢？这个时候需要找出206的子树，放到237的位置上的位置上去。

z是被覆盖的节点。

y是真正被delete的点

X是轴心点，以他为轴心

这里的删除也分为2种情况

1. 当要删除的节点，没有左右子树的情况，就只能删除父节点。

2. 第二种，就是上面分析的那点，实际要删除就是右子树上面的最小的那个点。

移除的节点是黑色，才有可能要调整。

为什么删除是4种情况？

//如果移除的节点是黑色的，这个时候需要调整void rbtree_delete_fixup(rbtree * T,rbtree_node * x){
 //黑色的点 while((x != T->root) && (x->color == BLACK)) { //如果是左子树 if(x == x->parrent->left) {
 rbtree_node *w = x->parrent->right; //如果右子树的颜色是红色 if(w->color == RED) { //改变作色 w->color = BLACK; x->parrent->color = RED;
 //左旋 rbtree_left_rotate(T,x->parrent); w = x->parrent->right;
 }
 //如果左子树是黑色，右子树是黑色 if((w->left->color == BLACK) && (w->right->color == BLACK)) {
 //改变作色 w->color = RED; //重新制定父节点 x = x->parrent;
 }else{
 //左子树不是黑色,右子树是黑色 if(w->right->color == BLACK) { //改变颜色
 w->left->color = BLACK; w->color = RED; //并右旋 rbtree_right_rotate(T,w); w = x->parrent->right; }
 //再左旋 w->color = x->parrent->color; x->parrent->color = BLACK; // w->right->color = BLACK; rbtree_left_rotate(T,x->parrent);
 x = T->root; }
 }else { //右子树 rbtree_node *w = x->parrent->left; if(w->color == RED) { w->color = BLACK; x->parrent->color = RED; //右旋 rbtree_right_rotate(T,x->parrent); w = x->parrent->left; }
 //如果左子树是黑色，右子树也是黑色 if((w->left->color == BLACK) && (w->right->color == BLACK)) { w->color = RED; x = x->parrent;
 }else { if(w->left->color == BLACK) { w->right->color = BLACK; w->color = RED; rbtree_left_rotate(T,w); w = x->parrent->left; }

 w->color = x->parrent->color; x->parrent->color = BLACK; w->left->color = BLACK; rbtree_right_rotate(T,x->parrent);
 x = T->root;
 }
 } }
 x->color = BLACK;}
rbtree_node *rbtree_delete(rbtree * T,rbtree_node * z){
 rbtree_node *y = T->nil; rbtree_node *x = T->nil; //如果当前只有一个节点 if((z->left == T->nil) || (z->right == T->nil)) { y = z; }else { //左右子树都不为空的情况 //寻找节点 y = rbtree_successor(T,z); }
 if(y->left != T->nil) { x = y->left;
 }else if(y->right != T->nil) { x = y->right; }
 x->parrent = y->parrent; if(y->parrent == T->nil) { //如果没有叶子节点 T->root = x;
 }else if(y == y->parrent->left) { y->parrent->left = x;
 }else { y->parrent->right = x; }
 if(y != z) { z->key = y->key; z->value = y->value; }
 //调整 if(y->color == BLACK) { rbtree_delete_fixup(T,x); }
 /* //如果这里重复写了，会出现内存段错误 if(y->color == BLACK) { rbtree_delete_fixup(T,x); }
 */

 return y;}

搜索红黑树节点

//搜索节点rbtree_node *rbtree_search(rbtree *T,KEY_TYPE key){
 rbtree_node *node = T->root; while(node != T->nil) { if(key < node->key) { //小于当前节点，插到左子树 node = node->left; }else if(key > node->key) { //大于当前节点，插到右子树 node = node->right; }else { return node;
 }
 } return T->nil;}

红黑树遍历

//查找红黑树最小值rbtree_node *rbtree_mini(rbtree *T,rbtree_node *x){ while(x->left != T->nil) { x = x->left;  }
 return x;}
//查找红黑树最大值rbtree_node *rbtree_maxi(rbtree *T,rbtree_node *x){ while(x->right != T->nil) { x = x->right; }
 return x;}
//中序遍历void rbtree_traversal(rbtree *T,rbtree_node *node){ if(node != T->nil) { //递归 rbtree_traversal(T,node->left); printf("key:%d, color:%d
", node->key, node->color); rbtree_traversal(T,node->right); }}
//增删改查测试代码int main(){ int keyArr[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};
 rbtree *T = (rbtree *)malloc(sizeof(rbtree)); if(T == NULL) {
 printf("malloc failed
"); return -1; }
 T->nil = (rbtree_node*)malloc(sizeof(rbtree_node)); T->nil->color = BLACK; T->root = T->nil;
 rbtree_node *node = T->nil; int i = 0; for(i = 0; i < 20; i++) {
 node = (rbtree_node*)malloc(sizeof(rbtree_node)); node->key = keyArr[i]; node->value = NULL; //插入 rbtree_insert(T,node);
 } //中序遍历 rbtree_traversal(T,T->root); printf("1----------------------------------------
"); for(i = 0; i < 20; i++) { //搜索 rbtree_node *node = rbtree_search(T,keyArr[i]); //删除 rbtree_node *cur = rbtree_delete(T,node); //释放 free(cur); //遍历 rbtree_traversal(T,T->root); printf("2----------------------------------------
"); }}

测试:

插入元素，然后中序遍历，并作色

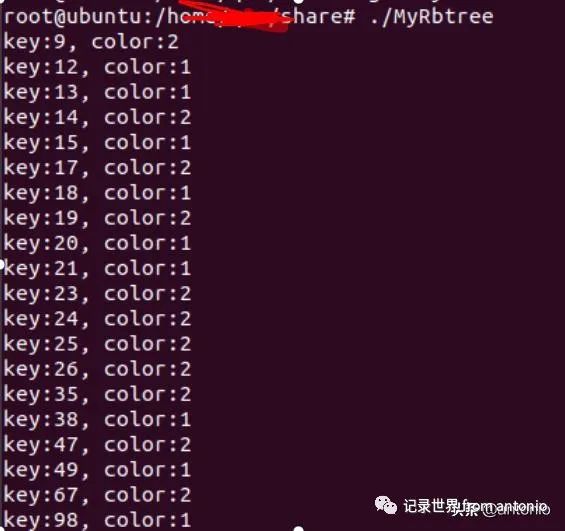
搜索，删除元素，再遍历输出

欢迎关注头条号