“红黑树”小结

Posted 2021-04-04 凌云网络实验室

    首先了解两个概念——“二分查找”和“树”。“二分查找”又称“折半查找”是一种效率较高的查找方法，而“树”是一种很常见的数据结构。由此，引出今天第一个主角二叉查找树(BST)。

二叉查找树

    二叉查找树：就是一颗二叉树，同时它的左节点比父节点要小，右节点比父节点要大。其基本操作有查找、遍历、插入和删除。

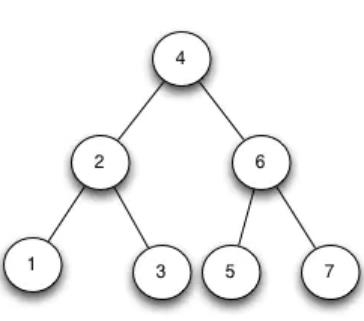
图一 平衡二叉查找树

    大家可能会发现BST中存在的问题：树在插入的时候会导致倾斜，不同的插入顺序会导致树的高度不一样，而树的高度直接影响了树的查找效率。最坏的情况所有的节点都在一条斜线上，这样树的高度为N。 

图二 倾斜二叉查找树

    基于BST存在的问题，平衡查找二叉树（Balanced BST）产生了。具有代表性的平衡树分别为高度平衡树(AVL：它具备二叉搜索树的全部特性，而且严格遵守左右子树高度差不超过1)和红黑树(仅需从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点即可)。但由于AVL树要求比较严格，插入和删除性能差，在实际环境下的应用不如红黑树。

    在正式介绍红黑树之前，我们先了解一下2-3-4树，这样有利于我们更好的理解红黑树。

2-3-4树

    2-3-4树是四阶的 B树(Balance Tree)，属于一种多路查找树，其结构有以下限制：

1. 所有叶子节点都拥有相同的深度。

2. 节点只能是 2节点、3节点、4节点之一。

    2节点：包含 1 个元素的节点，有 2 个子节点；3节点：包含 2 个元素的节点，有 3 个子节点；4节点：包含 3 个元素的节点，有 4 个子节点。所有节点必须至少包含1个元素。

3. 所有元素始终保持排序顺序，整体上保持二叉查找树的性质，即父结点大于左子结点，小于右子结点；而且结点有多个元素时，每个元素必须大于它左边的和它的左子树中元素。(将所有元素拍扁之后是有序的)

    其基本操作同二叉查找树。

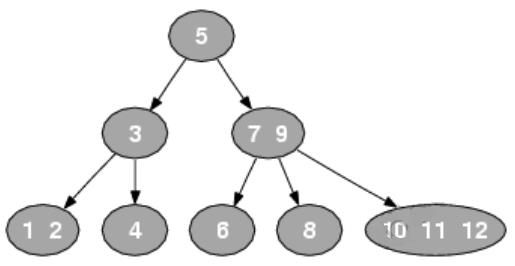
图三 2-3-4树

    红黑树可以由2-3-4树转化得到，2节点、3节点、4节点对应关系如图五所示：

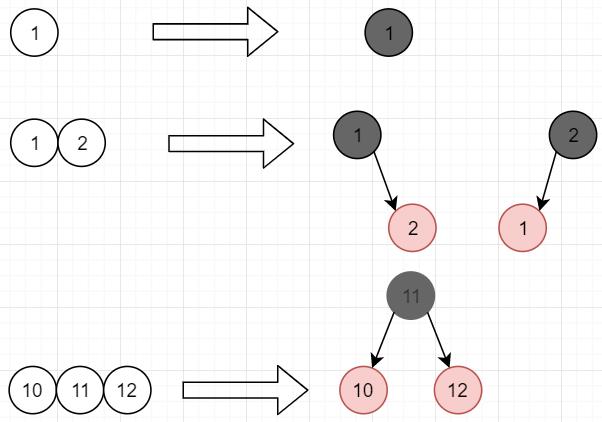
图五 节点对应关系

还有一种特殊的“裂变”状态，其对应特征如图六所示：

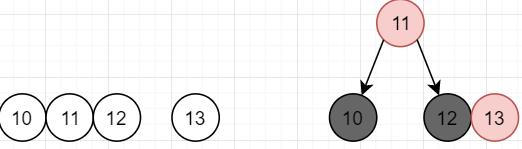
图六 “裂变”状态

因此，上文2-3-4树转化的红黑树如图七所示： 

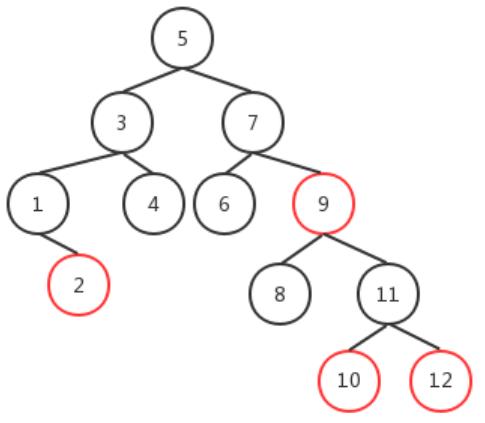
红黑树

    红黑树是一种结点带有颜色属性的二叉查找树，但它在二叉查找树之外，还有以下5大性质：

1. 节点是红色或黑色。

2. 根是黑色。

3. 所有叶子都是黑色（叶子是NIL节点，这类节点不可以忽视，否则代码会看不懂）。

4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）

5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点（黑色平衡）。

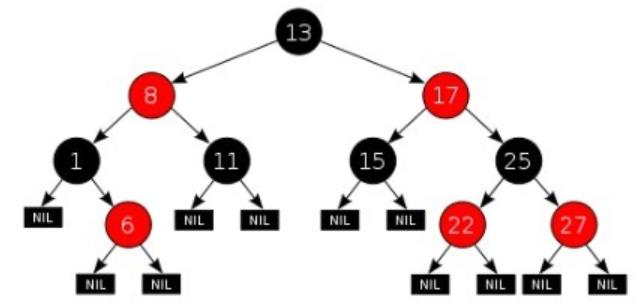
图四 红黑树

红黑树基本操作：

    由于红黑树在新节点插入前，总是平衡的，新节点的插入总是产生新层，破坏平衡。因此，红黑树为了保持平衡，有三个基本的操作：着色、左旋和右旋，其他操作(节点插入、删除)均是基于三个基本操作的。

1. 变色：节点的颜色由黑变红或者由红变黑

2. 左旋：以某个节点作为旋转点，其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，左子节点保持不变。

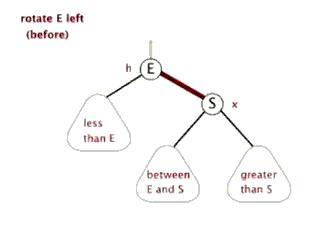
3. 右旋：以某个节点作为旋转点，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，右子节点保持不变。

4. 插入(以左子树为例)：分四种情况讨论，主要是要找到插入位置，然后通过左旋或者右旋且插入节点是红色。

①如果插入的是第一个节点（根节点），红色变黑色

②如果父节点为黑色，则直接插入，不需要变色

③如果父节点为红色，叔叔节点也是红色（此种情况爷爷节点一定是黑色），则父节点和叔叔节点变黑色，爷爷节点变红色（如果爷爷节点是根节点，则再变成黑色），爷爷节点此时需要递归（把爷爷节点当做新插入的节点再次进行比较）

④如果父节点是红色，没有叔叔节点或者叔叔节点是黑色（此时只能是NIL节点），则以爷爷节点为支点右旋，旋转之后原来的爷爷节点变红色，原来的父节点变黑色。

 

5. 删除：分三种情况讨论，自己搞定、父亲及兄弟帮忙、父亲及兄弟自损

①自己搞定：如果删除的节点对应于2-3-4树的3节点或者4节点，则直接删除；如果删除的是红色节点，则直接删；如果删除的是黑色节点，则红色节点上来替代，变黑即可。

②父亲及兄弟帮忙：找到“真正“的兄弟节点，兄弟节点有的借。

兄弟节点有两个子节点的情况（2个子节点肯定是红色，如果是黑色的话相当于此时兄弟节点对应2-3-4树是2节点，不可能有多余的元素可以借），此时需要旋转变色；兄弟节点只有一个子节点的情况，此时需要旋转变色。

③父亲及兄弟自损

 找到“真正“的兄弟节点，兄弟节点没的借（此时兄弟节点一定为黑色2节点），此时兄弟节点所在分支也要自损一个黑色节点以此达到黑色平衡，最快的方式就是兄弟节点直接变红（相当于就是减少一个黑色节点），此时一父节点为root的子树又达到了平衡（两边都比之前少一个黑

色）。但是以祖父节点为root的树依然是不平衡的，此时需要递归处理。

1

END

1

凌云网络实验室

图文：袁彤彤

排版：袁彤彤

审核：米玉秋