直方图均衡化

Posted 2023-04-19

参考技术A

想象一下，如果一副图像中的大多是像素点的像素值都集中在一个像素值范围之内会怎样呢？例如，如果一幅图片整体很亮，那所有的像素值应该都会很高。但是一副高质量的图像的像素值分布应该很广泛。所以你应该把它的直方图做一个横向拉伸（如下图），这就是直方图均衡化要做的事情。通常情况下，这种操作会改善图像的对比度。

这种方法通常用来增加许多图像的全局 对比度 ，尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法， 亮度 可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

这种方法对于背景和前景都太亮或者太暗的图像非常有用，这种方法尤其是可以带来 X光 图像中更好的 骨骼 结构显示以及曝光过度或者曝光不足 照片 中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是 可逆 操作，如果已知均衡化 函数 ，那么就可以恢复原始的直方图，并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择，它可能会增加背景 噪声 的对比度并且降低有用 信号 的对比度。

我们先来看看相应的直方图和累积直方图，然后使用 OpenCV 进行直方图均衡化。

我们可以看出来直方图大部分在灰度值较高的部分，而且分布很集中。而我们希望直方图的分布比较分散，能够涵盖整个 x 轴。所以，我们就需要一个变换函数帮助我们把现在的直方图映射到一个广泛分布的直方图中，这就是直方图均衡化。

**限制对比度自适应性直方图均衡化 CLAHE **

在上边做的直方图均衡化会改变整个图像的对比度，但是在很多情况下，这样做的效果并不好。的确在进行完直方图均衡化之后，图片背景的对比度被改变了。但是你再对比一下两幅图像中雕像的面图，由于太亮我们丢失了很多信息。

原理：

为了解决这个问题，我们需要使用自适应的直方图均衡化 CLAHE (Contrast Limited Adaptive Histogram Equalization)。这种情况下，整幅图像会被分成很多小块，这些小块被称为“tiles”（在 OpenCV 中 tileGridSize默认是 8x8），然后再对每一个小块分别进行直方图均衡化（跟前面类似）。所以在每一个的区域中，直方图会集中在某一个小的区域中（除非有噪声干扰）。如果有噪声的话，噪声会被放大。为了避免这种情况的出现，要使用对比度限制。

CLAHE中，每一个像素邻域都要进行对比度限制，从而得到对应的变换函数，被用来降低AHE中噪声的增强，这主要是通过限制AHE中的对比度增强来实现的。像素周围邻域噪声的增强主要是由变换函数的斜率造成的，由于像素邻域的噪声与邻域的CDF成正比，因此也与邻域直方图在该中心像素位置的值成正比，CLAHE之所以能够限制对比度，是因为它在计算邻域的CDF之前在指定阈值处对直方图进行了修剪，如下图所示，这一做法不仅限制了CDF的斜率，也限制了变换函数的斜率，其中对直方图进行切割所使用的阈值，被称作修剪限制度（clip limit），这个参数不仅依赖于直方图的归一化，而且依赖于像素邻域的size大小，通常设为3到4之间。

对于每个小块来说，如果直方图中的 bin 超过对比度的上限的话，就把其中的像素点均匀分散到其他 bins 中，然后在进行直方图均衡化。最后，为了去除每一个小块之间“人造的”（由于算法造成）边界，再使用双线性差值，与原图做图层滤色混合操作（可选）。

实现：

参考文献：
网址： 直方图均衡化
Adaptive_histogram_equalization
书籍：《数字图像处理》《OpenCV-Python 中文教程》

图片直方图均衡化

一、实验名称：直方图均衡化

二、实验内容

1、计算灰度图像归一化直方图

具体内容：利用Opencv对图像像素进行操作，就算归一化直方图，并在窗口以图形的方式展示出来。

2、灰度图的直方图均衡化处理

具体内容：通过计算归一化的直方图，设计算法实现直方图均衡化的处理。

3、彩色图像的直方图均衡化处理

具体内容：在灰度图像直方图均衡化的基础上实现彩色图像直方图均衡化的处理。

三、实验原理分析

3.1 实验原理

对于输入像素点r和输出像素点s都在灰度级 [0,L-1]之间，r = 0 代表黑色， r = L - 1代表白色。对于r和s的变换形式为：

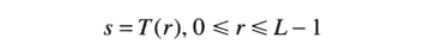
r和s满足一下条件：

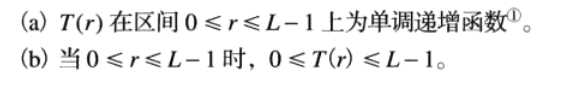
利用反函数来从s推r时，有以下定义：

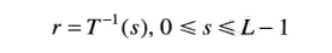
r和s满足条件：

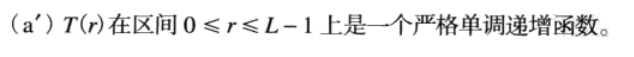
条件a是为了保证输出的灰度级不少于输入，这是为了防止二义性。条件b是为了保证输出的灰度范围和输入的灰度范围相同。条件a`也是为了保证s到r 也是一一对应的，防止二义性。实验中采用8bit整性的像素分布，不一定满足这个情况。

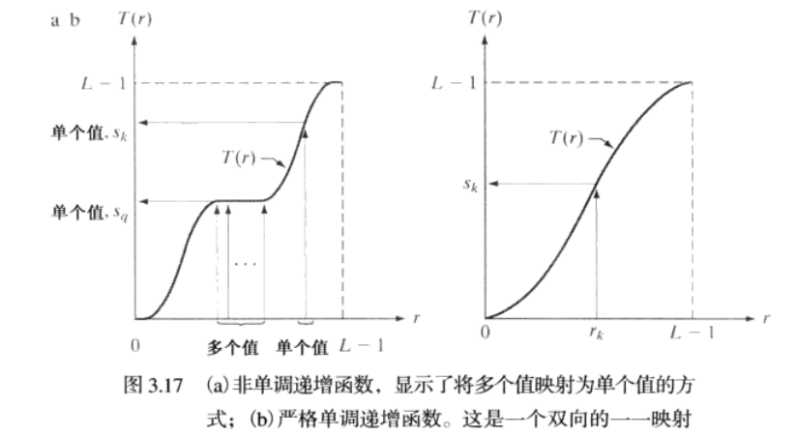
在实验中会类似左边的图像，出现多个输入的r,输出同一个s值。而在理论的约束上应该和右图相似，r与s一一对应。
对于一副灰度图像，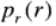
和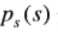
分别代表输入图像和输出图像的像素点的概率分布，我们简称为PDF。对于已知的和满足公式：

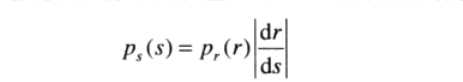
（1）
直方图均衡化的采用的公式如下：

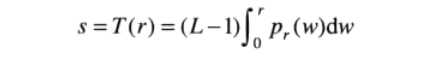
（2）
其中w是积分假变量，L-1是最大的灰度级。
为什么要这么做呢。由莱布尼兹准则，我们知道上限的定积分的导数是被积函数在该上限的值。

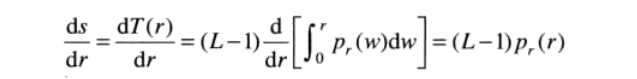
（3）
我们将的结果带入(1)中，

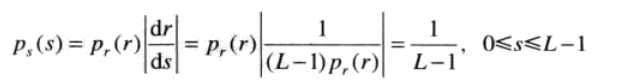
（4）

3.2 结论

使用（2）公式后，输出图像的像素点s分布是均匀的，PDF为1/(L-1)。

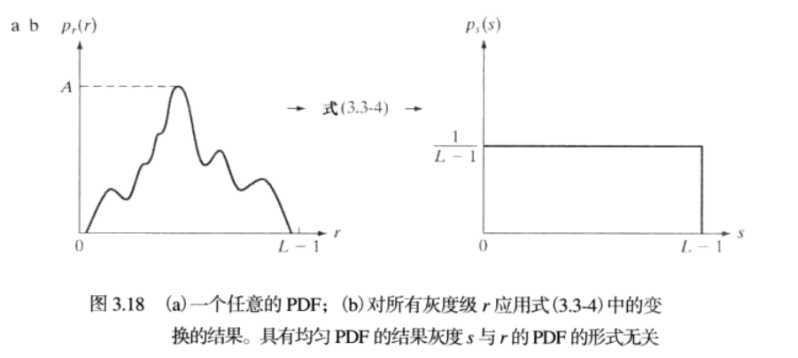
3.3 离散直方图均衡化采用公式

对于离散的直方图均衡化采用的公式为：

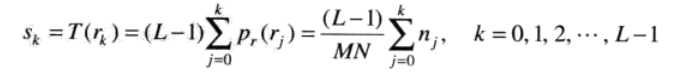
（5）
其中MN是总的像素点个数

四、编码实现

4.1 统计输入的灰度图像的像素信息

void calHistInfo(const Mat& src, vector<unsigned int>& calVec, vector<unsigned int >& calVecBefor,unsigned int LMax){
	int width = src.cols;
	int height = src.rows;
	int piexl = 0;
	for (int h = 0; h < height; h++) 
	{
		for (int w = 0; w < width; w++) {
			piexl = (int)src.at<uchar>(h, w);
			calVec[round(piexl)] += 1;
		}
	}
	
	calVecBefor[0] = calVec[0];
	for (int i = 1; i < calVec.size(); i++)
	{

		calVecBefor[i] = calVecBefor[i - 1] + calVec[i];
	}
	cout << "统计完毕" << endl;
}

这里我用了两个vector数组calVec 和calVecBefor ,calVec是用于记录每个灰度级别的像素个数，
calVecBefor是记录在当前像素r个数和r之前的像素之和。LMax是用于记录有多少个灰度级别，这里LMax =256。

4.2 根据直方图统计信息绘制折线图

void showHistChart(Mat& canvas,unsigned int LMax,vector<unsigned int> calVec,Scalar sca, int thikness)
{
//横轴是灰度级
//纵轴是像素的分布情况，我采取的方法是像素数目最多的为单位1
	int canvas_height = canvas.rows;
	int canvas_step = canvas.cols / LMax;
	auto it = max_element(calVec.begin(), calVec.end());
	unsigned int calMax = *it;

	//开始画折线图
	for (int i = 0; i < LMax-1; i++) 
	{
		line(canvas, Point(i * canvas_step, canvas_height - (canvas_height*(1.0)*calVec[i]/calMax)),
			Point((i + 1) * canvas_step, canvas_height - (canvas_height * (1.0) * calVec[i+1] / calMax)),
			sca, thikness, 8);
	}
}

其中canvas是画布，首先要找到像素点最多的灰度级别和该级别像素的个数calMax,以及根据画布大小和灰度级个数确定步长canvas_step，sca是画折线使用的颜色， thikness是折线的粗细，参数8是渲染方式。

4.3 确定像素点r与s之间的映射

void createRSTable(const vector<unsigned int>& calVecBefor,
	unordered_map<unsigned int,unsigned int>& table_rs,unsigned int LMax)
{
	double total = (double)calVecBefor[LMax - 1];
	for (int i =0;i<LMax;i++) 
	{
		double s = LMax*(double)calVecBefor[i] * (1.0) / total;
		if (round(s) <= 255) {
			table_rs.insert(make_pair(i, round(s)));
		}
		else 
		{
			table_rs.insert(make_pair(i, 255));
		}
		
	}
}

这里我采用的unordered_map用于记录输入的r与输出的s之间的映射关系。当然这里也可以用数组之类的记录，记录方法就是公式（5）。

4.4 灰度图像的直方图均衡化

void iHistImp(Mat& src, Mat&dst, unordered_map<unsigned int,unsigned int>& table_rs) {

	dst = Mat::zeros(src.size(), src.type());
	int width = src.cols;
	int height = src.rows;
	int piexl = 0;
	for (int h = 0; h < height; h++)
	{
		for (int w = 0; w < width; w++) {
			piexl = (int)src.at<uchar>(h, w);

				auto it = table_rs.find(piexl);
				if (it != table_rs.end())
				{
					dst.at<uchar>(h, w) = it->second;
				}

		}
	}
}

这里通过遍历灰度输入的输入像素点r,来找到相应的输出s。

4.5 灰度图像直方图均衡化的结果

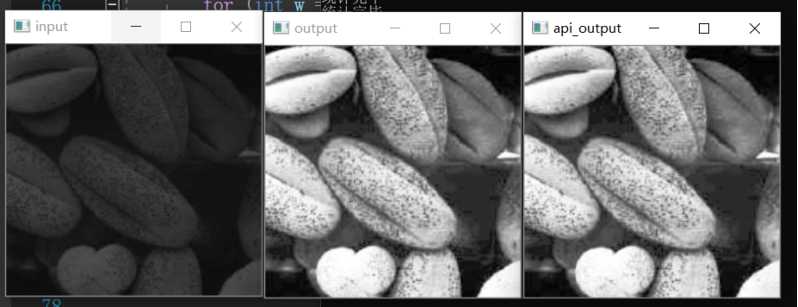
这里我除了使用自己实现的直方图均衡化，还调用opencv中直方图均衡化的api,来对比实验效果。
实验前后的折线图：

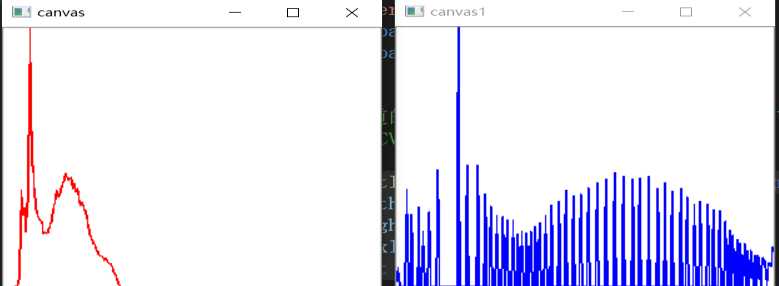
红色是直方图均衡化前的像素统计，蓝色是均衡化后的像素统计。

4.6 彩色图像的直方图均衡化

彩色图像的直方图均衡化，我是将输入的彩色图像分成bgr三个通道，分别进行直方图均衡化，然后再将结果合并再一起。

/*
* 彩色图像的直方图均衡化
*/
void BGRHist(Mat& src, Mat& dst) 
{
	//将彩色图像的按照BGR三个通道切分
	vector<Mat> splitMat;
	split(src,splitMat);

	//分别对bgr 三个通道进行直方图均衡化
	vector<Mat> mergeMat;
	split(src, mergeMat);
	for (int i = 0; i < 3; i++) 
	{
		unsigned int LMax = 256;
		vector<unsigned int> calVec(LMax, 0);
		vector<unsigned int > calVecBefor(LMax, 0);//用于记录灰度级l之前的所以的像素点个数
		calHistInfo(splitMat[i], calVec, calVecBefor, LMax);
		//构建输入像素r 与输出像素s 之间的 一一映射表
		unordered_map<unsigned int, unsigned int > table_rs;
		createRSTable(calVecBefor, table_rs, LMax);
		iHistImp(splitMat[i],mergeMat[i], table_rs);
	}
	merge(mergeMat,dst);
}

彩色图像直方图均衡化的结果：

五、实验中的问题以及需要改进的地方

1、在实验的像素的统计过程和r与s转换的过程，可以采用基于指针的方式遍历。

2、彩色图像的直方图均衡化效果不是很好，可以尝试新的算法。

3、r与s的映射表可以转成用数组存放，可能要快点。