怎么通俗易懂地解释EM算法并且举个例子？

Posted 2023-04-18

你知道一些东西（观察的到的数据），你不知道一些东西（观察不到的），你很好奇，想知道点那些不了解的东西。怎么办呢，你就根据一些假设（parameter）先猜（E-step），把那些不知道的东西都猜出来，假装你全都知道了;然后有了这些猜出来的数据，你反思一下，更新一下你的假设（parameter）,让你观察到的数据更加可能(Maximize likelihood;M-stemp);然后再猜，在反思，最后，你就得到了一个可以解释整个数据的假设了。1.注意，你猜的时候，要尽可能的猜遍所有情况，然后求期望（Expected）；就是你不能仅仅猜一个个例，而是要猜出来整个宇宙；2.为什么要猜，因为反思的时候，知道全部的东西比较好。（就是P(X,Z)要比P(X)好优化一些。Z是hidden states）3.最后你得到什么了？你得到了一个可以解释数据的假设，可能有好多假设都能解释数据，可能别的假设更好。不过没关系，有总比没有强，知足吧。（你陷入到local minimum了）

公司有很多领导=[A总，刘总，C总]，同时有很多漂亮的女职员=[小甲，小章，小乙]。（请勿对号入座）你迫切的怀疑这些老总跟这些女职员有问题。为了科学的验证你的猜想，你进行了细致的观察。于是，观察数据：1）A总，小甲，小乙一起出门了；2）刘总，小甲，小章一起出门了；3）刘总，小章，小乙一起出门了；4）C总，小乙一起出门了；收集到了数据，你开始了神秘的EM计算：初始化，你觉得三个老总一样帅，一样有钱，三个美女一样漂亮，每个人都可能跟每个人有关系。所以，每个老总跟每个女职员“有问题”的概率都是1/3;这样，（E step）1）A总跟小甲出去过了1/2*1/3=1/6次，跟小乙也出去了1/6次；（所谓的fractional count）2）刘总跟小甲，小章也都出去了1/6次3）刘总跟小乙，小章又出去了1/6次4）C总跟小乙出去了1/3次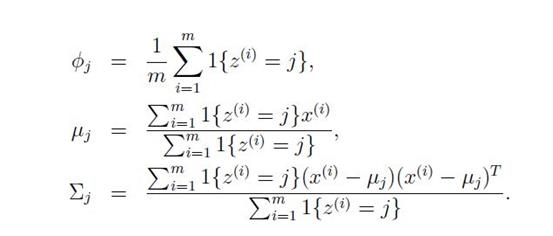

参考技术A

最大似然估计和EM算法都是根据实现结果求解概率分布的最佳参数θ，但最大似然估计中知道每个结果对应哪个概率分布（我知道哪个概率分布实现了这个结果），而EM算法面临的问题是：我不知道哪个概率分布实现了该结果。怎么在不知道其概率分布的情况下还能求解其问题？一般的用Y表示观测到的随机变量的数据，Z表示隐随机变量的数据(因为我们观测不到结果是从哪个概率分布中得出的，所以将这个叫做隐变量)。于是Y和Z连在一起被称为完全数据，仅Y一个被称为不完全数据。这时有没有发现EM算法面临的问题主要就是：有个隐变量数据Z。而如果Z已知的话，那问题就可用极大似然估计求解了。于是乎，怎么把Z变成已知的？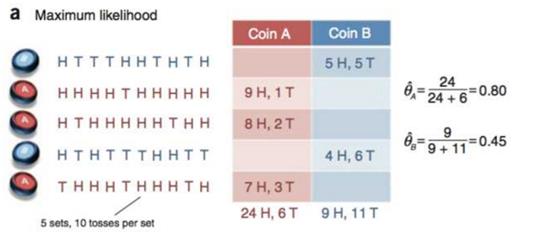

参考技术B

现在一个班里有50个男生，50个女生，且男生站左，女生站右。我们假定男生的身高服从正态分布，女生的身高则服从另一个正态分布：。这时候我们可以用极大似然法（MLE），分别通过这50个男生和50个女生的样本来估计这两个正态分布的参数。但现在我们让情况复杂一点，就是这50个男生和50个女生混在一起了。我们拥有100个人的身高数据，却不知道这100个人每一个是男生还是女生。这时候情况就有点尴尬，因为通常来说，我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。但从另一方面去考量，我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。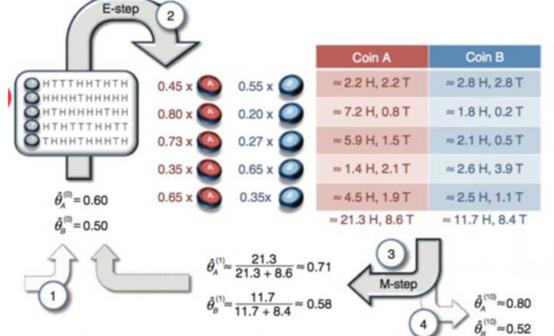

Ceph 通俗易懂的解释 Crush 算法

http://www.xuxiaopang.com/2016/11/08/easy-ceph-CRUSH/