机器学习——分类学习

Posted 2021-04-03 蜗牛的灯塔

一、设置问题  

针对于图片数据，因为图像时高维度数据，贸然开始处理会很难。因此，根据图片特征分类为纵向图像和横向图像。

二分类:二分类问题 - simplehearted - 博客园 (cnblogs.com)

假设现在有两个训练数据：

宽	高	形状
80	150	纵向
160	50	横向

（可讲数据表示在平面直角坐标中，x轴为图像的宽、y轴为图像的高）

但是数据太少，下面我们进行相应增加：

宽	高	形状
80	150	纵向
60	110	纵向
35	130	纵向
160	50	横向
160	20	横向
125	30	横向

如果只用一条先将途中白色的点和黑色的点分开

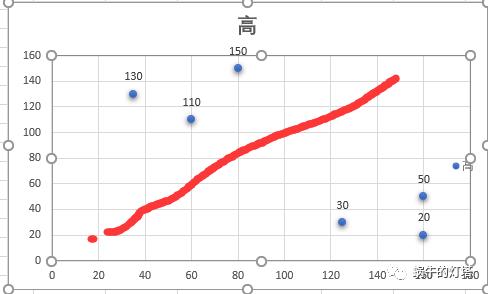
分类的目的就是找到这条红色的分界线。根据点在线的上方还是下方，从而对其形状进行分类。

二、内积  

目的是找出向量。分类用图形来解释更容易理解，所以将其想象为由大小和方向的、带箭头的向量比较好。

如内容一图，所画线是使权重向量成为法线向量的直线。设权重向量为ω，那么那条直线的表达式为：

                                                                  

权重向量就是我们想要知道的未知参数，ω是权重一词的英文——weight的首字母。同回归一样，θ和ω一样，目的就是求未知参数。θ和ω都是参数，只是叫法不一样。

表达式（3.2.1）是两个向量的内积。实向量空间的内积是各相应元素乘积的和，因此可将表达式改写为：

                                           

法线是与某条直线相垂直的向量。

接下来以n=2，ω=（1，1）为例，进行解释：

                                                 

在移项变形之后，表达式变成x2=-x1。就是斜率为-1的直线

内积的另一个表达式：

                                                          

表达式中|ω|和|x|是向量的长，因此必定是正数。要想使内积为0，只能使cosθ=0，即θ=90°或者θ=270°。

在计算之后，最终找到与我画的直线成直角的权重向量就行

小结：在一开始并不存在所画的直线，二十要通过训练找到权重向量，然后才能得到与这个向量垂直的直线，最后根据这条直线就可以对数据进行分类。