机器学习选股模型的可解释性分析

Posted 2021-04-03 量化投资与机器学习

全网Quant都在看！

编译：QIML编辑部

在上一篇文章中：

 

MF框架从Linear、Nonlinear及Interactions三个角度，分别对模型的以下两个方面进行了分析：

 

1、每个因子在模型中的作用：

• 线性部分（Linear）和非线性部分（Nonlinear）对模型效果的贡献；

• 每两个因子之间相互作用（Interactions）对模型效果的贡献。

2、模型应用到投资组合中，最终收益率的拆分，也是分为Linear、Nonlinear及Interactions三个部分。

 

我们分别从以上两个应用来解释MF框架：

Part1：MF框架

量化每个因子在模型预测结果中的边际贡献

在把每个因子的效果拆解为Linear、Nonlinear及Interactions三部分之前，我们首先要掌握一个重要的概念：模型对于每个因子的边际依赖。Friedman (2001)提出了partial dependence的概念，主要为了测算每个单独的因子对于模型效果的影响程度。具体的做法是，选定某个待分析的因子k，每次对于所有的样本点，固定k的值而其他因子值不做变动，测试k在不同取值情况下模型效果的变化。如果非要用数学公示加以表达，以下公式就是Partial Dependence Eqution，表示在保持其他因子不变的情况下，因子k在不同取值时，模型效果的期望：

在机器学习工具库Scikit-Learn中，有现成的分析Partial dependence的函数，plot_partial_dependence。以下图1，就反应了在房价预测这个案例中，AveOccup及HouseAge的边际贡献。

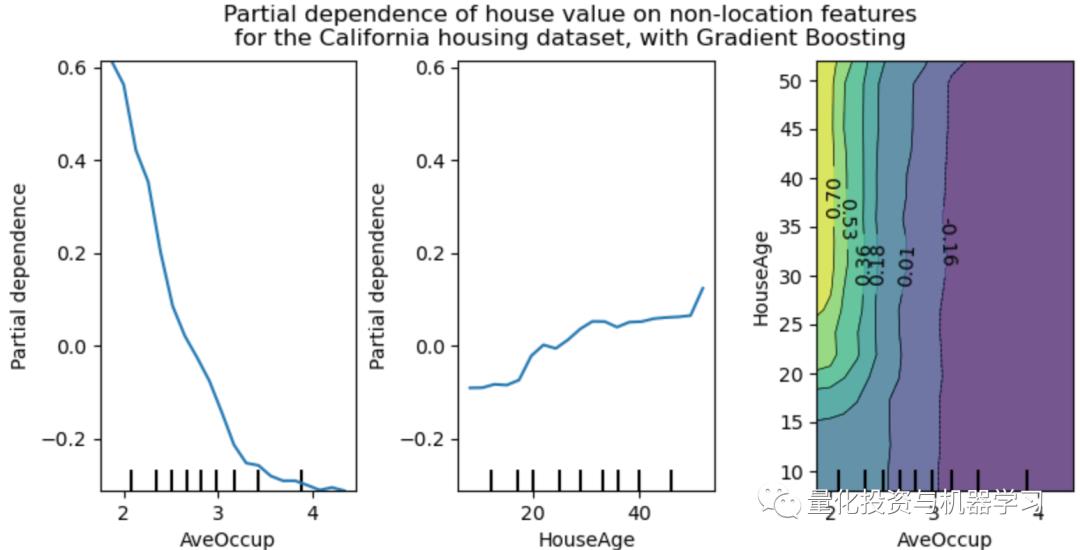
从"因子"到“收益率”的预测，机器学习模型的应用一直非常直观，但通常我们很难理解模型背后的逻辑，更别说把模型的机制进行可视化。在这篇文章中，我们参考partial dependence的理念，尝试从以下三个角度去分析机器学习模型的预测机制：Linear、Nonlinear和Interactions。

以下公式中，l函数为线性partial dependence function（假设预测模型为普通线性回归模型），f函数为原始模型。

• Linear prediction effect: 因子k的线性贡献用。k在某个固定取值时，线性模型对于k的边际依赖，减去原始模型对于k的边际依赖的平均值，再对这个差的绝对值求均值。

  
  

• Nonlinear prediction effect：因子k的非线性贡献，等于原始模型f对于k的边际依赖，减去线性模型对于k的边际依赖，得到的差的绝对值的均值就是模型对于k的非线性依赖。（换个角度就是因子对于模型效果的非线性影响）

• Interactions effect：两个因子交互作用的贡献，等于原始模型f对于两个因子整体的边际依赖，减去原始模型f对于两个因子分别的依赖，再求这个差的绝对值的均值。

Pairwise interaction effect 

关于interactions effect的定义，作者参考了 Friedman and Popescu (2008)的H-statistic.

下图1展示了某个模型对于某个因子三个方面的依赖，从左到右分别是Linear、Nonlinear和Interactions。

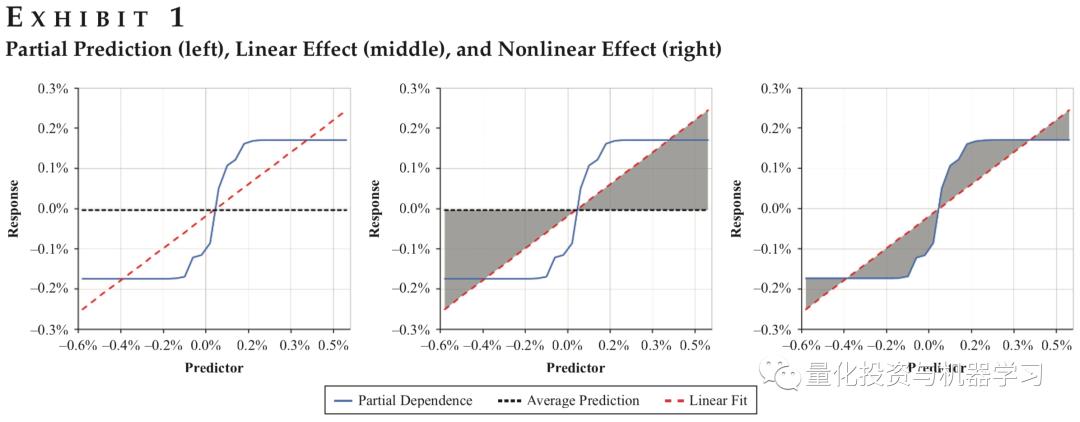
图2展示了模型对于两个因子交互作用的依赖，可以看出当因子1极高（或极低）且因子2极低（或极高）时，模型的效果较佳。

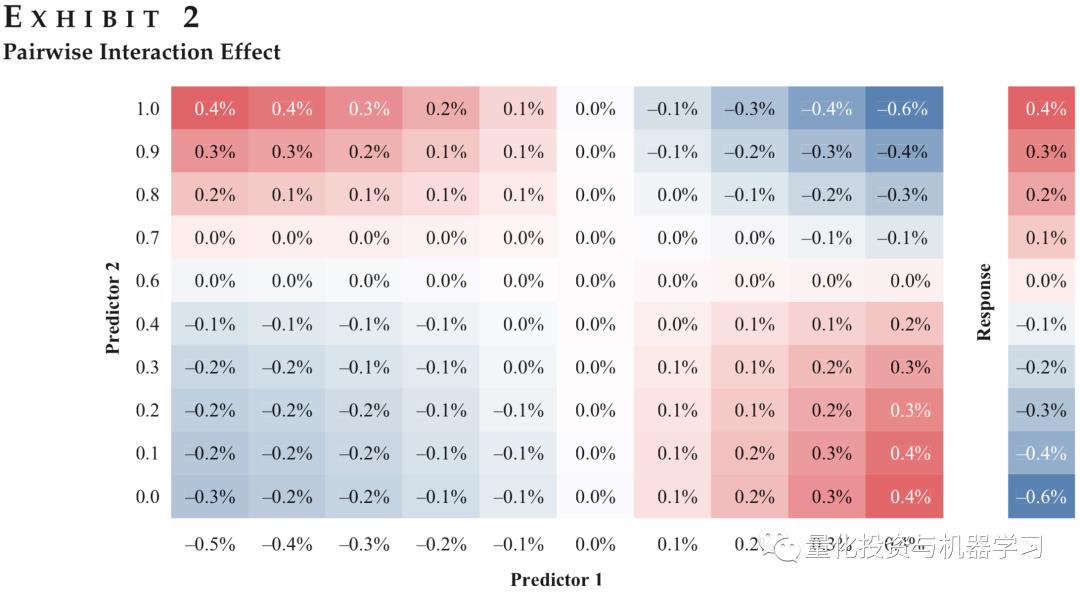
计算模型对于某个因子边际依赖的具体步骤如下：

1、固定因子K的值，用模型预测不同样本的预测目标；

2、对于该因子K在这个特定值下，对于所有样本的预测结果，计算评价指标（如R平方）；

3、改变K的取值，再次计算评价指标，就可以做出如图1的Partial Dependence Plot。

Part2：MF框架

从Linear、Nonlinear及Interactions三个角度拆解收益

Part1中，我们从模型预测效果的角度对每个因子的边际贡献，从Linear、Nonlinear及Interactions的三个角度进行了拆解结分析。但我们最终关系的是模型反映到策略端时的最终收益. 这一部分，我们综合各个因子的三方面的边际贡献，把模型的收益拆分为线性收益（Linear）、非线性收益（Nonlinear）、交互收益（Interactions）及高维度交互收益（Higher-order Interactions）。

关于如何测算所有因子不同作用的收益，作者没有详细阐述，小编结合文章内容做一下猜测。假设现在有S1、S2、S3、S4、S5五只股票，及X1、X2、X3三个因子，及已经校准好的线性模型L：

1、固定X1因子的值，用线性模型L分别预测五只股票的下一期收益；

2、改变X1的值，再用线性模型L分别预测五只股票的下一期收益；

3、对以上每只股票，在X1不同取值下的预测求平均，记为R1

4、在对因子X2、X3重复1-3的步骤，求出R2、R3；

5、求R1、R2及R3的均值，在根据这个均值对股票进行排序，构建组合。

以上组合的收益就是线性收益。

 

1、线性收益是各因子线性贡献部分带来的收益，计算方法参数以上注释。

2、相互作用来的的收益，等于相互作用及线性贡献带来的收益减去步骤1中的线性收益。

3、非线性收益，等于线性、相互作用及非线性贡献带来的收益减去步骤1和2的收益。

4、高维相互作用带来的收益，等于模型的总收益减去步骤1-3的收益。

 

 

通过以上步骤，我们就可以把根据一个模型预测结果构建的投资组合的收益拆分为Linear、Nonlinear及Interactions三个主要的部分，剩下的解释不了的部分，我们放在高维相互作用带来的收益。

Part3：实证分析

作者用G10国家的10个外汇币种组成的45对外汇组合（以下称为品种），并基于以下5个因子构建预测模型，预测目标是每组外汇未来1个月的收益，并基于这个预测选出27个预测收益绝对值最大的品种。然后根据选出品种的预测收益方向，相应的做多或做空。五个因子是：

 

1、The short-term interest rate differential between countries

2、The trailing five-year spot return adjusted for trailing five-year inflation differential

3、The trailing one-year spot return

4、The trailing one-year equity return differential

5、 Currency market turbulence

 

选取了常用的几种机器学习模型：Random forests、Gradient boosting machines和Neural networks. 训练时间为1990年至2015年，测试时间为2016年至2019年。测试结果参考下图。在所有模型中，interest rate differential的非线性贡献最大，同时interest rate differential与Currency market turbulence的交互作用带来的贡献，也是所有因子对中最大的。图4更清楚了展示了不同取值时，这两者交互作用给模型带来的贡献。我们还可以看出，Random Forests中，各因子各个维度的贡献都不是很明显；GB中模型可多的挖掘了因子的非线性作用，而Neural Network中更多的挖掘了因子的线性作用。

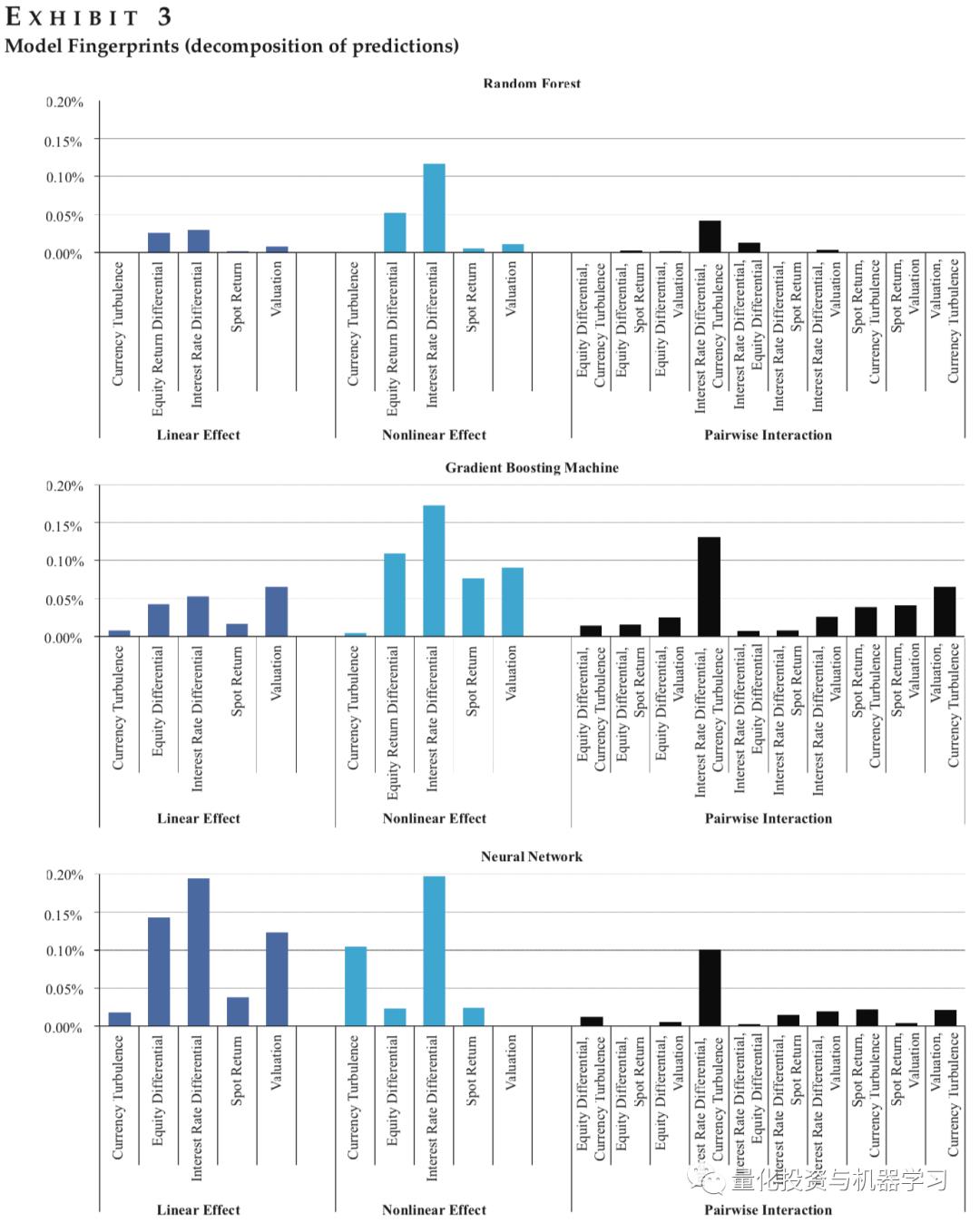
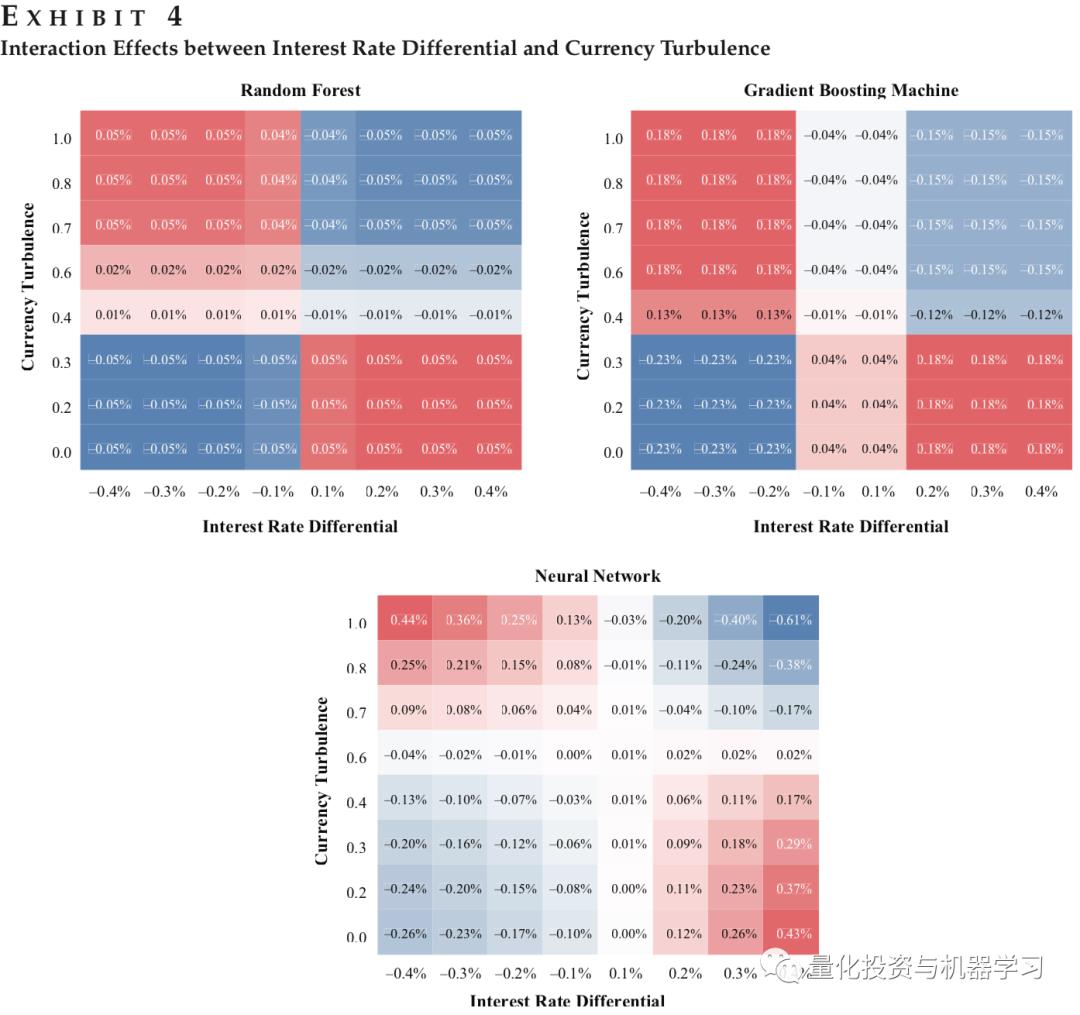
图5展示了训练集中，各模型收益的拆解，可以看出，线性收益占了各个模型收益的绝大部分，GB模型更擅长挖掘因子间相互作用（包括高维相互作用），Neural Network更擅长挖掘非线性收益。

最后，给出了不同模型在样本内外的测试表现，不同模型的效果样本内外保持的比较一致，整体而言GB模型和Neural Networks的表现更优。

总结

从Linear、Nonlinear及Interactions三个角度分析因子在不同模型中的贡献，首先可以看出不同因子的特点，其次也能看出模型在不同维度挖掘信息的强弱，比如GB模型擅长挖掘因子交互作用带来的信息，Neural Network擅长挖掘单因子的非线性信息。最终，从可解释的角度拆解因子的贡献及模型的收益，能够指导我们更好的选择模型及因子。

参考文献：

1、Friedman, J. H., and B. E. Popescu. 2008. “Predictive Learning via Rule Ensembles.” The Annals of Applied Statistics 2 (3): 916–954.

2、Li, Y., Turkington, D. and Yazdani, A., 2020. “Beyond The Black Box: An Intuitive Approach to Prediction with Machine Learning.” The Journal of Financial Data Science, Vol. 2, No. 3

(Summer).