机器学习 | 最大熵模型学习的最优化算法

Posted 2021-04-03 BBIT

机器学习 | 最大熵模型学习的最优化算法（一）

今天我们来说最大熵模型学习中用到的最优化算法：改进的迭代尺度法。

我们知道最大熵的模型为：

其中：

对数似然函数为：

目标是通过极大似然估计学习模型参数求对数似然函数的极大值 。

改进的迭代尺度法的想法是：假设最大熵模型最大熵模型当前的参数向量是 ，找到一个新的参数向量 ，使模型的对数似然函数值增大。如果能有这样一种参数向量更新的方法 ，那么就可以不停迭代，直至找到对数似然函数的最大值。

因为：

所以：

利用不等式 可知：

又知：

则

又因为：

于是：

这里，将等式右端记为 ，这是似然函数的下界。

如果我们能够找到适当的 使下界提高，那么似然函数也会随之提高。但 是一个向量，不易同时对每个方向都进行优化，于是固定其它方向，仅优化其中的一个方向，这时我们需要再一次更新下界，使得可以仅优化一个方向。

具体的，我们引入一个量：

这个值表示所有特征在(x, y)中出现的次数，其可能为常数也可能不为常数。原因如下：

首先这个函数 本身代表的是一个规则，即 与 满足某一事实，则为1，否则为0。括号内的 和 是输入值，即每一个数据点的数据，或者说是每一个实例的数据。

那么 中的下标i表示的是不同的规则，比如 在x=1, y=2的情况下为1，否则为0； 在x=2，y=2的情况下为1，否则为0。

对某一个实例而言，我们将其代入 和 中，判断这个实例的数据是否符合 和 的规则，如果仅符合 而不符合 ， 。

那么 实际上是对一个特定的实例的数据进行i次不同规则的判断，这就是其即可能为常数也可能不为常数的原因。在常数的情况下，说明每一个实例的数据符合的规则的数量是一样的，比如有三个规则，实例1符合规则1和规则2，实例2符合规则2和规则3，实例3符合规则1和规则3，尽管它们符合的规则不同，但数量相同，三个实例的f#(x, y)都为2。当然，f#(x, y)为常数的情况发生的概率很小，因此f#(x, y)在大部分情况下都不是常数。

回到算法本身，定义了f#(x, y)之后，可以将 进行改写，于是，最终得到了：

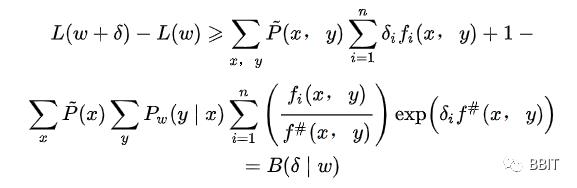
于是下界被再一次刷新，此时可以对向量 中的一个方向单独进行优化（求导）了。对其求偏导并令导数为0：

于是有：

这样就可以依次对每一个 求解，得到向量 并对 进行更新迭代。

以上就是今天的内容，谢谢大家的观看！