机器学习入门之决策树1

Posted 2021-04-03 雲知的B612

分而治之

此处重点放在分而治之的解题思路

问题1: 给定一个数组 [2,3,4,6]，你需要将这些数字相加，并返回结果。

使用循环很容易完成这种任务：

num = [2,3,4,6]def sum1(num): total = 0 for i in num: total += i return total
print(sum1(num))15

问题2: 那我们如何使用 分而治之 策略呢？

Q1: 如果我问数组[2] or []数字相加的结果是多少？

A1: 2 or 0，因为只有1个元素时，累加肯定是其本身2；没有元素时，肯定为0。因此，称这种情况下为基线条件。可以理解为：计算最简单的条件。

Q2：对于数组[2,3,4,6]求和是否可以看成：对数组[2]求和 + 对数组[3,4,6]求和？

A2：可以，在问题2中，所求取的数组长度更短了。换言之，这缩小了问题规模，这就是Divide。

综合问题1和问题2，新的sum2函数工作原理如下：

1. 如果列表为空，返回0

2. 否则，计算第1个元素+剩余元素列表总和

def sum2(num): if num == []: return 0 return num[0] + sum2(num[1:])print(sum2(num))15

总结1：¶

1. 分而治之不是用于解决问题的算法，而是一种解决问题的思路。

2. 首先要找到基线条件。

3. 每次递归调用都必须离基线条件更进一步，即 缩小问题规模。

决策树基本流程¶

决策树（Decision Tree）是一类常见的机器学习算法，其基本流程图遵循简单且直观的 D&C策略。

下面以西瓜问题来展示决策树基本流程：

西瓜属性包含：[色泽, 根蒂, 敲声]

1. 我们可能首先看“它是什么颜色的？”，如果是“青绿色”

2. “它的根蒂是什么形态？”，如果是“蜷缩”

3. “它敲起来是什么声音？”，如果是“浊响”

结论：好瓜。

对照 D&C策略，我们发现下一次的问题总是基于属性子集来问的。第一个问题包含3种属性，第二个问题包含2种属性，等等。

由此可见，决策树是基于树结构来进行决策的。这种决策方式恰是人类在面临决策问题时一种很自然的处理机制。并且我们会很容易理解每个决策步骤的结果（有很好的解释性）。

一般的，一颗决策树：

• 包含一个根节点（包含所有属性）

• 若干内部节点（跟节点属性子集）

• 若干叶节点（最终决策结果：好瓜or坏瓜）

从根节点到叶节点的一条路径，称之为“一个决策序列”。

决策树伪代码¶

三种情形¶

1. 当前节点包含的样本全属于同一类别，无需划分（红色框）。

2. 当前属性集为空，或是所有样本在所有属性上取值相同（x取值一样），无法划分（蓝色框），根据少数服从多数投票（后验分布）。

3. 当前节点包含的样本集合为空，不能划分（绿色框），此时要回到上一节点，根据少数服从多数投票（先验分布）。

注：由于决策树是采用 分而治之策略，所以决策树的生成是一个递归过程。

划分选择¶

信息熵（information entropy）

在上面绿色框内有一个红色小框（第8行），如何选择最优划分属性呢？

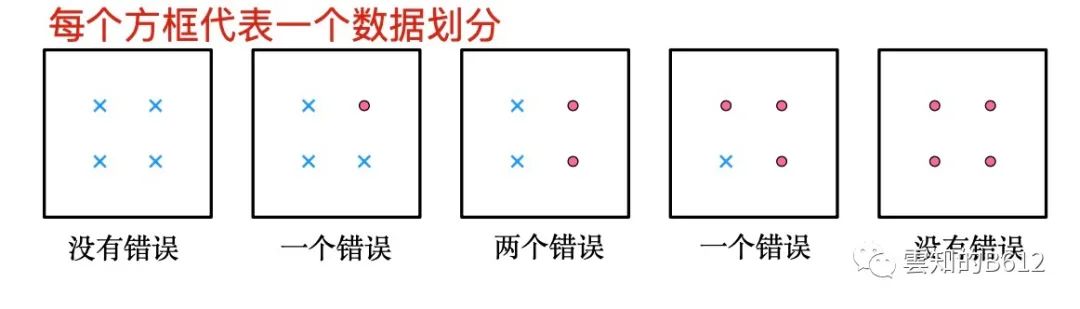
我们应该如何衡量一个划分数据的犯错大小呢？

从上面的图片可以看出：当两类东西数量相当时，我们不能用少数服从多数投票方法给出结果。

如何衡量一类东西数量相对整体的情况呢？

我们可以用频率，根据统计学知识，我们知道一个东西频率的极限就是概率。

但是如果单用概率，我们很难描述上述图片。（从左到右依此为数据集1-数据集5）

• 第1个数据集，x类概率为4/4，红点类为0/4

• 第2个数据集，x类概率为3/4，红点类为1/4

• 第3个数据集，x类概率为2/4，红点类为2/4

• 第4个数据集，x类概率为1/4，红点类为3/4

• 第5个数据集，x类概率为0/4，红点类为4/4

我们会发现，如果单纯使用概率值，我们需要指定其值是对应那类数据。

但是如果我们只看类别情况，第1个数据集与第5个数据集有区别吗？第2个数据集与第4个数据集有区别吗？

虽然数据集1与数据集5、数据集2与数据集4，两类数据占比情况有所区别；但是所传递的信息量是一样的

1. 数据集1和数据集5都只有一类数据

2. 数据集2和数据集4，都是有一类数据占比3/4，有一类数据占比1/4

所以为了描述上述图片的区别，我们要采用信息量来描述。

在1948年，香农在 A Mathematical Theory of Communication 论文中首次对上述信息量做了定量描述：信息熵。

信息熵：是对一个信号源所发出的符号（x号和红点）的不确定性的定量描述

公式为：