PNN神经网络(Matlab)
Posted 您好啊数模君
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PNN神经网络(Matlab)相关的知识,希望对你有一定的参考价值。
一、介绍
概率神经网络它主要用于模式分类,是径向基网络的一个分支,是基于贝叶斯策略前馈神经网络。它具有如下优点:学习过程简单、训练速度快;分类更准确,容错性好等。从本质上说,它属于一种有监督的网络分类器,基于贝叶斯最小风险准则。
二、PNN结构
该神经网络与GRNN类似由输入层、隐含层和输出层组成。输入层将变量传递给隐含层,但不进行计算,因此该层只起传输数据的作用。隐含层中的神经元个数等于训练集样本个数,该层的权值函数为欧式距离函数,用||dist||表示,其作用是计算出网络输入与输入层权重IW1,1之间的距离及阈值,阈值用b1表示。隐含层传递函数为径向基函数,采用高斯函数作为网络的传递函数。输出层为竞争输出,各神经元依据Parzen方法来球和估计各类的概率,从而竞争输入模式的响应机会,最后仅有一个神经元竞争获胜,这样获胜的神经元即表示对输入变量的分类。
在数学上,PNN结构的特性,可在高维数据空间中解决在低维空间不易解决的问题。也因此其隐含神经元较多,但隐含层空间的维数和网络性能有着直接的关系,维数越高,网络的逼近精度越高,但带来的负面后果是网络复杂度也随之提高。
三、算法步骤
(1)确定隐含层神经元径向基函数中心
设训练集样本输入矩阵P和输出矩阵T

其中,pij表示第j个训练样本的第i个输入变量;tij表示第j个训练样本的第i个输出变量;n为输入变量的维度;k为输出变量的维度;m为训练集样本数。
隐含层的每个神经元对应一个训练样本,即m个隐含神经元对应的径向基函数中心
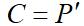
(2)确定隐含层神经元阈值
m个隐含神经元对应的阈值为:
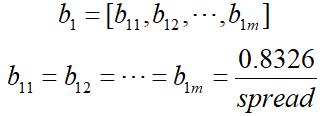
spread为径向基函数的扩展速度。
(3)确定隐含层与输出层的权值
隐含层神经元的径向基函数中心及阈值确定后,隐含层神经元的输出可有下式计算:
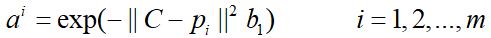
其中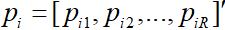 为第i个训练样本向量。
为第i个训练样本向量。
隐含层与输出层间的连接权值W取为训练输出矩阵,即
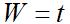
(4)输出层神经元输出计算
当隐含层与输出层神经元间的连接权确定后,即可计算出输出层神经元输出。
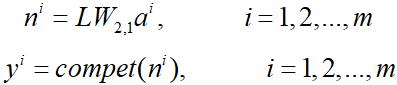
案例——对某花不同种类的识别
本文给出一些已经确定好的花的各个种类的各项特征数据,请对其余花种的类别进行识别。
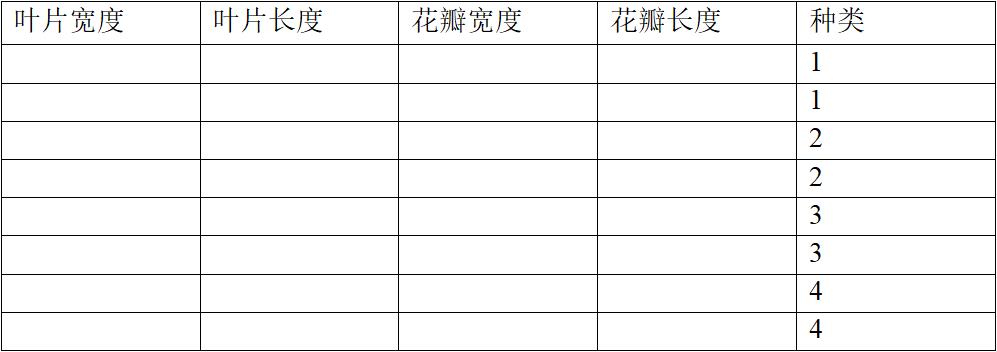
由于数据较多,本文不列举,首先先在matlab导入两个数据矩阵,一个是花种的各项指标数据,一个是花的类别。
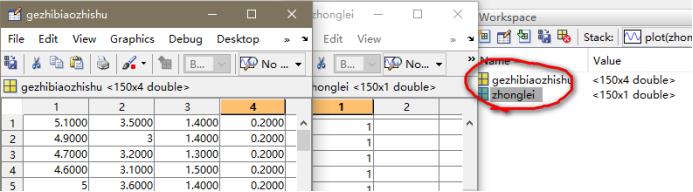
mat数据文件保存:
将数据读入matlab后键入
>>save+空格+名称 比如:
>>save shuju
即将当前Workspace工作区间中的所有矩阵文件保存在shuju.mat文件中
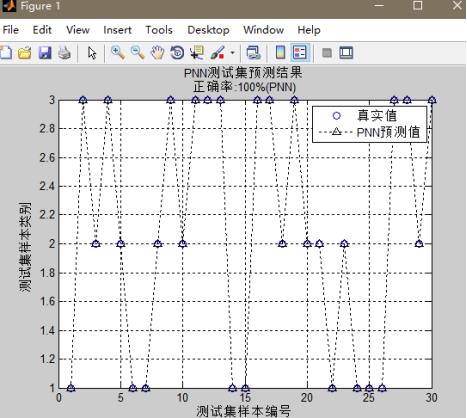
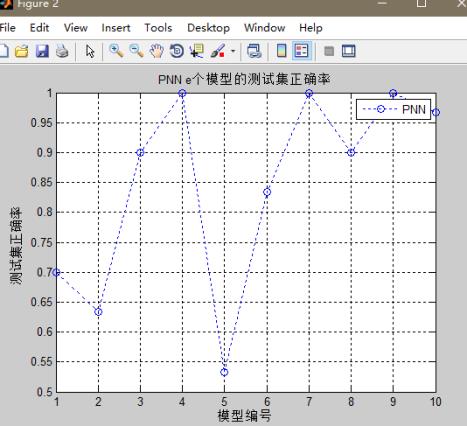
%% 清空环境变量clear allclc%% 训练集/测试集产生% 导入数据load shuju.mat[a,b]=size(gezhibiaozhishu);%指标矩阵维度% 随机产生训练集和测试集,这里是在标准数据中随机选取一部分用来训练,一部分用于检验P_train = [];%初始化矩阵T_train = [];%初始化矩阵P_test = [];%初始化矩阵T_test = [];%初始化矩阵g = gezhibiaozhishu;z = zhonglei;n = randperm(a);%函数功能:随机打乱一个数字序列c=120;%用于训练的个数d=30;%用于检验的个数% 训练集——提取矩阵前c个样本P_train = g(n(1:c),:)';T_train = z(n(1:c),:)';% 测试集——提取矩阵后d个样本P_test = g(n(c+1:a),:)';T_test = z(n(c+1:a),:)';%% 模型建立result_grnn = [];%初始化矩阵result_pnn = [];%初始化矩阵time_grnn = [];%初始化矩阵time_pnn = [];%初始化矩阵for i = 1:bfor j = i:b%这里提取p_train = P_train(i:j,:);p_test = P_test(i:j,:);%% PNN创建及仿真测试t = cputime;Tc_train = ind2vec(T_train);% 创建网络net_pnn = newpnn(p_train,Tc_train);% 仿真测试Tc_test = ind2vec(T_test); %ind2vec详见后文解释t_sim_pnn = sim(net_pnn,p_test);T_sim_pnn = vec2ind(t_sim_pnn); %vec2ind详见后文解释t = cputime - t;time_pnn = [time_pnn t];%记录每次运行的时间result_pnn = [result_pnn T_sim_pnn'];%记录每次运行的结果endend%% 性能评价% 正确率accuracyaccuracy_pnn = [];%记录pnn的正确率time = [];%记录grnn和pnn每个模型运行的时间e=(b^2+b)/2;%e为建立模型的个数for i = 1:eaccuracy_2 = length(find(result_pnn(:,i) == T_test'))/length(T_test);accuracy_pnn = [accuracy_pnn accuracy_2];end[~,good]=max(accuracy_pnn);% 结果对比result = [T_test' result_pnn];accuracy = accuracy_pnn;time = time_pnn;%% 绘图figure(1)plot(1:d,T_test,'bo',1:d,result_pnn(:,good),'k:^')grid onxlabel('测试集样本编号')ylabel('测试集样本类别')string = {'PNN测试集预测结果';['正确率:' num2str(accuracy_pnn(good)*100) '%(PNN)']};title(string)legend('真实值','PNN预测值')figure(2)plot(1:e,accuracy(1,:),'b:o')grid onxlabel('模型编号')ylabel('测试集正确率')title('PNN e个模型的测试集正确率')legend('PNN')figure(3)plot(1:e,time(1,:),'b:o')grid onxlabel('模型编号')ylabel('运行时间(s)')title('PNN e个模型的运行时间')legend('PNN')

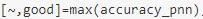
ind2vec和vec2ind明白其中一个,反之另一个就明白了,先说容易理解的vec2ind吧,从命令名字上可以看出是“向量变索引”,假设一个3*6的稀疏矩阵T(1,:)=[0 1 0 0 1 0];T(2,:)=[1 0 1 1 0 0];T(3,:)=[0 0 0 0 0 1],通过vec2ind(T)将会得到什么?因为通过矩阵知道T是6列的,vec2ind(T)得到的记过是1行6列的向量,该向量对应的元素分别是T中第1列到第6列中数字"1"对应的行号,因例子中的T矩阵,在第一列中第2行对应的是"1",则vec2ind(T)的第一个元素是2,同理,T中第二列中“1”在第1行,则vec2ind(T)的第二个元素是"1",依次类推,T中第3列至第6列中“1”对应行数分别是“2","2","1","3",因此,vec2ind(T)=[1 2 2 2 1 3];
ind2vec则反过来理解即可,如一个索引适量A=[1 3 2 2 2 1 2 1],求ind2vec?从A可以看出A是1行8列的(如果实在不知道,就用size(A)查看),从A中元素最大值"3"可以看出,索引对应的向量是3行的,还不理解?那就用最基本的方法,因A中元素对应的是行号,设B=ind2vec(A),意味着B(1,1),B(3,2),B(2,3),B(2,4), B(2,5), B(1,6),B(2,7),B(1,8)对应的值是"1",其余元素均为"0"
即
以上是关于PNN神经网络(Matlab)的主要内容,如果未能解决你的问题,请参考以下文章