机器学习笔记#1 线性回归
Posted Yuan的学习笔记
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习笔记#1 线性回归相关的知识,希望对你有一定的参考价值。
Yuan的学习笔记 作者 Yuan
-
什么是线性模型 -
线性模型的基本形式 -
线性回归 -
多元线性回归 -
Python模拟
什么是线性模型?

还是用周志华老师的西瓜来举例子吧,假如我们有很多西瓜,我们要给西瓜打分,西瓜有这些属性(色泽,敲声,大小等),线性模型通过这些属性的线性组合来判断一个瓜好不好。
线性模型的基本形式
线性模型(linear model)试图学得一个通过属性(x1;x2;...;xd)的线性组合来进行预测的函数,即
特点:
-
线性模型形式简单,易于建模 -
许多功能强大的非线性模型可在线性模型的基础上通过引入层级结构或高位映射而得 -
线性模型由很好的可解释性
线性回归
给定数据集,线性回归试图学得一个线性模型以尽可能准确地预测输出值。
即线性回归试图学得
确定w和b的关键在于如何衡量f(x)与y之间的差别。均方误差是回归任务中最常用的性能度量,可以试图让均方误差最小化,即:
求解w和b使E(w,b)
最小化的过程,称为线性回归模型的最小二乘“参数估计”。将E(w,b)分别对w和b求导,得到:
令上面两个式子为零可得到w和b的最优解:
其中:
多元线性回归
下面看更一般的情形,我们有数据集D,m个样本,每个样本有d个属性。此时线性回归试图学得:
这称为多元线性回归。
还是用最小二乘法对w和b进行估计。我们把w和b吸收入向量:
把数据集D表示为一个m*(d+1)大小的矩阵X:
Tips: 矩阵X每行对应一个样本,每行前d个元素对应d个属性值; 一共m个样本所以有m行; b前的系数为1,所以每行最后一个元素恒置为1;
也可以写成这样:
再把标记(每个样本的label,或真实值)也写成向量形式:
类似于公式(1.4),我们试图求解均方误差最小化的w:
我们令
令上式为零得到w的最优解。
Notice: 这个戴帽子的w已经包含了w和b
当X^TX为满秩矩阵或正定矩阵,令(1.10)式为零可得:
令xi^hat = (xi;1),最终学得的多元线性回归模型为:
然而许多任务中变量的数目会超过样例数(对应X矩阵列数大于行数,m<d),导致X^TX不满秩。此时,我们可以解出多组使均方误差最小化的解。
Tips: 其实就是解方程的时候,未知数个数多于方程数,结果有好多解。
Python模拟
来看点有趣的吧,我们用python模拟下,看看公式(1.11)是否可以求出线性回归模型的参数w和b,使所有样本到直线上的欧氏距离之和最小。
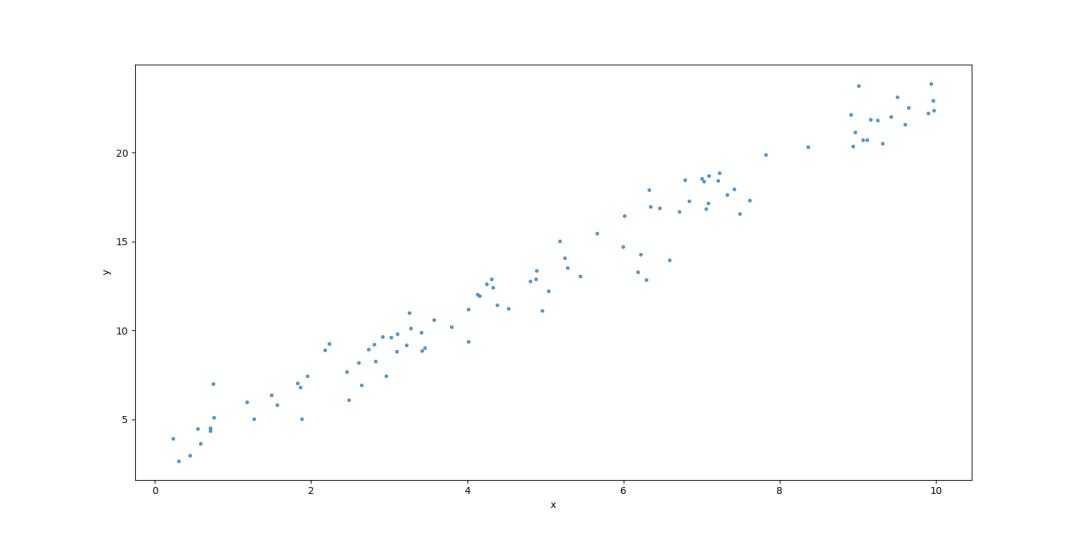
先导入numpy库,使用np.random.rand生成100个0到10之间的随机数,样本标记是y(y = 2 * x + 3 + 满足标准正态分布的随机数)。
In [1]: import numpy as np
In [2]: x = np.random.rand(100, 1) * 10
In [3]: y = 2 * x + np.random.randn(100, 1) + 3
Tips: np.random.rand随机生成0到1之间的数 np.random.randn随机生成满足标准正态分布的数
使用matplotlib库函数查看生成的样本:
In [4]: import matplotlib.pyplot as plt
In [5]: plt.figure(figsize=(10,8))
...: plt.scatter(x, y, s = 8, alpha = 0.7)
...: plt.xlabel('x')
...: plt.ylabel('y')
...: plt.show()
按照公式(1.11)求得线性回归模型的参数w和b
In [6]: X = np.concatenate((x, np.ones((100,1))), axis=1)
In [7]: w_and_b = np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T, X)), X.T), y)
In [8]: w_and_b
Out[8]:
array([[2.02609688],
[3.01087005]])
Tips: np.concatenate可以将两个矩阵在某一个维度拼接 np.matmul用于矩阵相乘 np.linalg.inv可以求矩阵的逆
求得参数w是2.02609688,参数b是3.01087005,我们把这条线画出来:
In [9]: plt.figure(figsize=(10,8))^M
...: plt.scatter(x, y, s = 8, alpha = 0.7)^M
...: plt.plot(x, w_and_b[0]*x+w_and_b[1], c='yellow')^M
...: plt.xlabel('x')^M
...: plt.ylabel('y')^M
...: plt.show()
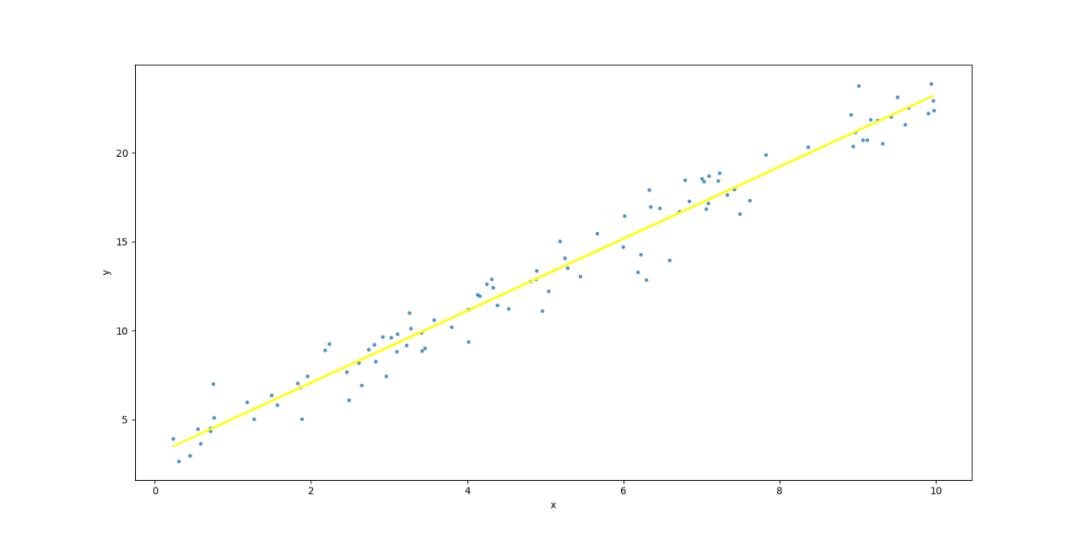
这样我们就找到了一条线,使所有样本到直线上的欧氏距离(均方误差)之和最小。
以上是关于机器学习笔记#1 线性回归的主要内容,如果未能解决你的问题,请参考以下文章