二叉树红黑树以及Golang实现红黑树
Posted 算法爱好者
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树红黑树以及Golang实现红黑树相关的知识,希望对你有一定的参考价值。
=> x==> logn。
那么为什么会出现退化成链表的情况(图一)呢?我们该怎么处理才不会变成链表呢(怎么解决)?
当插入的节点数值从小到大时,则就会出现二叉树退化成链表的情况,那么有另一种树可以解决这种情况,就是平衡二叉树(AVL树)。
AVL树是一种追求极致平衡的二叉搜索树,即将树调整到最优的情况,由于这种树结构比较苛刻、旋转也比较多,这里就不重点展开讲。
1. 变颜色的情况:如果插入的节点的父节点和叔叔节点为红色,则:1)把父节点和叔叔节点设为黑色;2)把爷爷(祖父)节点设为红色;3)把指针定位到爷爷节点作为当前需要操作的节点,再根据变换规则来进行判断操作。2. 左旋:如果当前父节点是红色,叔叔节点是黑色,而且当前的节点是右子树时,则需要以父节点作为左旋转。3. 右旋:当前父节点是红色,叔叔节点是黑色,且当前的节点是左子树时,则:1)把父节点变为黑色;2)把爷爷节点变为红色;3)以父节点右旋转。
比如要往上图中插入数字6,则这颗红黑色的演变过程如下:
step1: 插入6节点后如下图,它的父节点和叔叔节点均是红色,则需要根据变换规则来操作,到step2了。

step2: 根据变换规则,需要将插入节点的父节点和叔叔节点均变为黑色,爷爷节点变为红色,然后将指针定位到爷爷节点(蓝色圈)。将指针定位到爷爷节点(12)后,此时做为当前需要操作的节点,再根据变换规则来判断,可以看到下图的当前节点(12)的叔叔节点是黑色的,则不能用变颜色规则的情况了,进行step3,此时需要进行左旋或右旋了。

step3: 根据上图情况可以知道此时是符合左旋规则的:当前节点(12)的父节点(5)是红色,叔叔节点(3)是黑色,而且当前的节点是右子树。接下来需要进行左旋变换(三步走):

step4:左旋变换后,可以看到当前节点(5)的父节点(12)为红色,叔叔节点(30)为黑色,而且当前节点为左子树,符合右旋的规则。接下来就是进行右旋的变换操作了:1)把父节点(12)变为黑色;2)把爷爷节点(29)变为红色;3)以父节点(12)右旋转

到这里,可以看到经过多次旋转后,这棵树是符合红黑色的性质。
Golang代码实现红黑树直接上代码,如下:
package main
import (
"fmt"
"math/rand"
"time"
)
const (
RED bool = true
BLACK bool = false
)
type Node struct
key int
value interface
left *Node
right *Node
//parent *Node
color bool
type RedBlackTree struct
size int
root *Node
func NewNode(key, val int) *Node
// 默认添加红节点
return &Node
key: key,
value: val,
left: nil,
right: nil,
//parent: nil,
color: RED,
func NewRedBlackTree() *RedBlackTree
return &RedBlackTree
func (n *Node) IsRed() bool
if n == nil
return BLACK
return n.color
func (tree *RedBlackTree) GetTreeSize() int
return tree.size
// node x
// / \\ 左旋转 / \\
// T1 x ---------> node T3
// / \\ / \\
// T2 T3 T1 T2
func (n *Node) leftRotate() *Node
// 左旋转
retNode := n.right
n.right = retNode.left
retNode.left = n
retNode.color = n.color
n.color = RED
return retNode
// node x
// / \\ 右旋转 / \\
// x T2 -------> y node
// / \\ / \\
// y T1 T1 T2
func (n *Node) rightRotate() *Node
//右旋转
retNode := n.left
n.left = retNode.right
retNode.right = n
retNode.color = n.color
n.color = RED
return retNode
// 颜色变换
func (n *Node) flipColors()
n.color = RED
n.left.color = BLACK
n.right.color = BLACK
// 维护红黑树
func (n *Node) updateRedBlackTree(isAdd int) *Node
// isAdd=0 说明没有新节点,无需维护
if isAdd == 0
return n
// 需要维护
if n.right.IsRed() == RED && n.left.IsRed() != RED
n = n.leftRotate()
// 判断是否为情形3,是需要右旋转
if n.left.IsRed() == RED && n.left.left.IsRed() == RED
n = n.rightRotate()
// 判断是否为情形4,是需要颜色翻转
if n.left.IsRed() == RED && n.right.IsRed() == RED
n.flipColors()
return n
// 递归写法:向树的root节点中插入key,val
// 返回1, 代表加了节点
// 返回0, 代表没有添加新节点, 只更新key对应的value值
func (n *Node) add(key, val int) (int, *Node)
if n == nil // 默认插入红色节点
return 1, NewNode(key, val)
isAdd := 0
if key < n.key
isAdd, n.left = n.left.add(key, val)
else if key > n.key
isAdd, n.right = n.right.add(key, val)
else
// 对value值更新,节点数量不增加,isAdd = 0
n.value = val
// 维护红黑树
n = n.updateRedBlackTree(isAdd)
return isAdd, n
func (tree *RedBlackTree) Add(key, val int)
isAdd, nd := tree.root.add(key, val)
tree.size += isAdd
tree.root = nd
tree.root.color = BLACK //根节点为黑色节点
// 前序遍历打印出key,val,color
func (tree *RedBlackTree) PrintPreOrder()
resp := make([][]interface, 0)
tree.root.printPreOrder(&resp)
fmt.Println(resp)
func (n *Node) printPreOrder(resp *[][]interface)
if n == nil
return
*resp = append(*resp, []interfacen.key, n.value, n.color)
n.left.printPreOrder(resp)
n.right.printPreOrder(resp)
// 测试红黑树代码
func main()
count := 10
redBlackTree := NewRedBlackTree()
nums := make([]int, 0)
for i := 0; i < count; i++
nums = append(nums, rand.Intn(count))
fmt.Println("source data: ", nums)
now := time.Now()
for _, v := range nums
redBlackTree.Add(v, v)
fmt.Println("redBlackTree:", now.Sub(time.Now()))
redBlackTree.PrintPreOrder()
fmt.Println("节点数量:", redBlackTree.GetTreeSize())
测试输出结果如下:
data source: [1 7 7 9 1 8 5 0 6 0]
redBlackTree: -2.136µs
[[7 7 false] [1 1 true] [0 0 false] [6 6 false] [5 5 true] [9 9 false] [8 8 true]]
节点数量: 7
红黑树是保持近似平衡的二叉树,从另一种角度上来说红黑树不是平衡二叉树,它的最大高度为2*logn。
二分搜索树,AVL树,红黑树对比:1. 对于完全随机的数据源,普通二分搜索树很好用,缺陷是在极端情况下容易退化成链表 2. 对于查询较多的使用情况,AVL树很好用,因为他的高度一直保持h=logn 3. 红黑树牺牲了平衡性,即h=2*logn,但在添加和删除操作中,红黑树比AVL树有优势 4. 综合增删改查所有操作,红黑树的统计性能更优
zhuanlan.zhihu.com/p/368944960
- EOF -
1、一些著名的软件都用什么语言编写?
2、“阿里味” PUA 编程语言火上 GitHub 热榜
3、深入理解 CPU 的调度原理
觉得本文有帮助?请分享给更多人
推荐关注「算法爱好者」,修炼编程内功
点赞和在看就是最大的支持❤️
二叉树红黑树
封装基于 BinaryTreeOperations 的 红黑树(一种自平衡的二叉查找树)。
除了提供 BinaryTreeOperations 中的部分基础接口外,增加按键的插入 和 按键或节点指针的删除操作。
在阅读本文前,您应该先了解二叉树中的旋转是怎么回事(相关文章很多且简单,笔者不再赘述)。
讲解红黑树的教程很多,但是很多讲解并不足以让读者清楚的学会红黑树,尤其是删除操作,许多教程十分凌乱,因此本文将使用清晰的层次分类及必要的图进行讲解。
节点定义:
enum class Color :bool { RED = 0, BLACK }; struct Node { _Ty key; Node* left = nullptr; Node* right = nullptr; Node* parent = nullptr; Color color = Color::RED; Node(const _Ty& _key) :key(_key) {} };
红黑树的规则:
① 每个节点是红色或者黑色。
② 根节点是黑色。
③ 每个叶子节点是黑色(注意:这里的叶子节点指 为空的叶子节点)。
④ 如果一个节点是红色,则它的孩子必须是黑色(或者说支路上不得出现连续的红节点)。
⑤ 从任意节点到其叶子节点的所有路径中,所办含的黑色节点数相同(叶子节点同样指为空的节点)。
请务必尽快熟练的记住以上规则(尤其是 ②,④,⑤),尽管这看似复杂,但在应用中正是因为这些特性会使得红黑树没这么难。
红黑树的增删操作分为两步:
① 按二叉查找树的规则将节点插入到相关位置。
② 讨论各种情况,若红黑树失衡则采取相关方法进行调整使之重新恢复平衡。
插入操作(令插入的节点为 cur,cur 的父节点为 par,par 的兄弟节点为 uncle,par 的父节点为 gpa):
如嵌套 if else 一样,我们将插入情况分为两类(称为外层分类),再根据这两类的 子情况 进行其他分类(称为内层分类)。
注意,新插入节点 cur 一定是红色(因为这不会违背规则 ⑤,只有可能违背规则 ① ④,违背 ① 时容易处理,即插入空树时只需将其变为黑色即可)。
为何宁愿违背 ① ④ 而不宁愿违只背 ⑤(即新插节点是黑色)?(你可以理解为这会更容易实现自平衡,不用过于纠结)。
插入空树情况比较简单,后文不特地说明该情况。
① 外层分类分为:par 是黑色 或 par 是红色。
② 内层分类是在 par 是红色 的情况下分类的,这在稍后进行讲解。
现在先解决 ①:
1) par 是黑色时,直接插入即可(这不会打破平衡)。
2)par 是红色(打破规则 ④),进入 ②。(注:此时 gpa 一定是黑色,看规则 ④)。
现在解决 ② (分为 uncle 是红色 或 uncle 是黑色):
1)如图 uncle 是红色时(空的黑色节点没有画出):
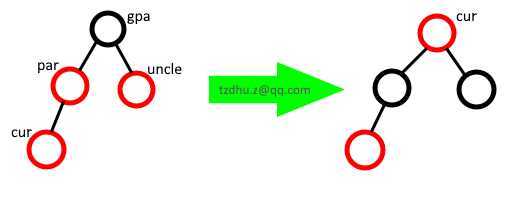
如图进行变色后将 cur 指向 gpa 的节点,继续执行 1)。
直到 cur 是红色且为根节点时,直接将根节点变黑即可。或者出现 新的 uncle 是黑色 时进入后面的情况。
2)uncle 是黑色时分为四类情况(不用担心,原理都一样,分为两类也可以的,这里也可以类似 AVL 树四种旋转情况)该情况调整后便已经平衡,可直接返回。
① 直接看图,图中给出 par 是左孩子的两种情况:
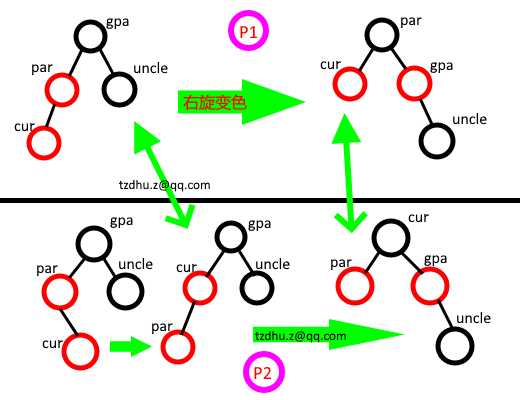
图上P1,以 gpa 右旋(看!是不是类似 AVL 树的 左左_右旋!),并交换 par 和 gpa 的颜色(小的两类情况是:cur 是左孩子还是右孩子)。
图下P2,先将 gpa 的左孩子左旋,在将 gpa 右旋(看!是不是类似 AVL 树的 左右_左右旋!),然后交换 cur 和 gpa 的颜色。
② 接下来,par 是右孩子的两种情况(小的两类情况同样看 cur 是左孩子还是右孩子)。
由于 ② 与 ① 是左右对称的情况,因此交给读者自行思考(用 AVL 树的旋转方法类似的话是:右右_左旋 和 右左_右左旋),不需要笔者继续画图了吧!
至此,插入操作结束!总结......就不用了吧。接下去是删除操作,情况很多,坐稳扶好!!!(不用慌,笔者会以清晰的层次进行分类说明)。
删除操作:
待续......
以上是关于二叉树红黑树以及Golang实现红黑树的主要内容,如果未能解决你的问题,请参考以下文章