机器学习矩阵运算必学库Numpy首秀！

Posted 2022-02-01 机器学习算法那些事

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习矩阵运算必学库Numpy首秀！相关的知识，希望对你有一定的参考价值。

[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]])

       [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.]]])

[0., 0., 0., 0.],
[0., 0., 0., 0.]])

      [0., 2., 0., 0.],
       [0., 0., 0., 1.]])

[1., 1.],
[1., 1.]])

       [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]]])

[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])

      [0, 1, 0, 0],
       [0, 0, 1, 0],
       [0, 0, 0, 1]])

[1., 1., 1.]])

      [1, 1, 1]])

[4, 5, 6]])

      [4., 5., 6.]])

[6, 5, 4]])
[7, 8, 9]])
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]])

      [1., 0., 0., 0., 0., 1.],
       [1., 0., 0., 0., 0., 1.],
       [1., 0., 0., 0., 0., 1.],
       [1., 0., 0., 0., 0., 1.],
       [1., 1., 1., 1., 1., 1.]])

[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1.]])

      [0., 1., 1., 1., 1., 1., 1., 0.],
       [0., 1., 1., 1., 1., 1., 1., 0.],
       [0., 1., 1., 1., 1., 1., 1., 0.],
       [0., 1., 1., 1., 1., 1., 1., 0.],
       [0., 1., 1., 1., 1., 1., 1., 0.],
       [0., 1., 1., 1., 1., 1., 1., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0.]])

[1, 0, 0, 0, 0, 0],
[0, 2, 0, 0, 0, 0],
[0, 0, 3, 0, 0, 0],
[0, 0, 0, 4, 0, 0],
[0, 0, 0, 0, 5, 0]])
[0.34963774, 0.51837142],
[0.68895046, 0.04980068]],

[[0.98352437, 0.47189043],
[0.30430488, 0.49057744],
[0.20020709, 0.90466043]]])
[9, 8, 7, 6]])
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])

      [ 8,  9, 10, 11, 12, 13, 14, 15]])

      [ 2,  3],
       [ 4,  5],
       [ 6,  7],
       [ 8,  9],
       [10, 11],
       [12, 13],
       [14, 15]])

      [ 2,  3],
       [ 4,  5],
       [ 6,  7],
       [ 8,  9],
       [10, 11],
       [12, 13],
       [14, 15]])

      [ 8,  9, 10, 11, 12, 13, 14, 15]])

5.99484250e+02, 1.66810054e+03, 4.64158883e+03, 1.29154967e+04,
3.59381366e+04, 1.00000000e+05])

11.75787594, 21.77264 , 40.3174736 , 74.

Numpy快速上手（机器学习基础）

「这是我参与2022首次更文挑战的第5天，活动详情查看： 2022首次更文挑战」

本博文优先在掘金社区发布！

前言

刚才我已经演示了，机器学习的常用的绘图库之一的matplotlib。那么接下来使我们另一个经常使用的numpy。numpy的使用相当广泛，所以不论你是不是学习机器学习，其实都是要学的当然还有一个库pandas也是我们需要掌握的（不过这个库内容稍微比较多，同样的使用pandas可以帮助我们对数据进行清洗）

在进行机器学习，或者数学运算时，我们经常需要使用到矩阵，那么numpy就为我们提供了很多类似的功能。并且numpy的使用相当简便，而且速度相当之快，相对于python自带的list而言，numpy由于底层是C语言直接避免了GIL的限制，支持并行运算，同时相对于list的存储模式，numpy更像是一个数组。

请注意我这里使用的环境是jupyter
速度对比

import random 
import time import numpy as np 
a = [] 
for i in range(100000000): 
    a.append(random.random()) 
# 通过%time魔法方法, 查看当前行的代码运行一次所花费的时间 
%time sum1=sum(a) 
b=np.array(a) 
%time sum2=np.sum(b)

numpy基本操作

首先numpy的使用和我们的list的使用类似。区别只是在api的使用上面略有区别。

此外支持的数据类型有

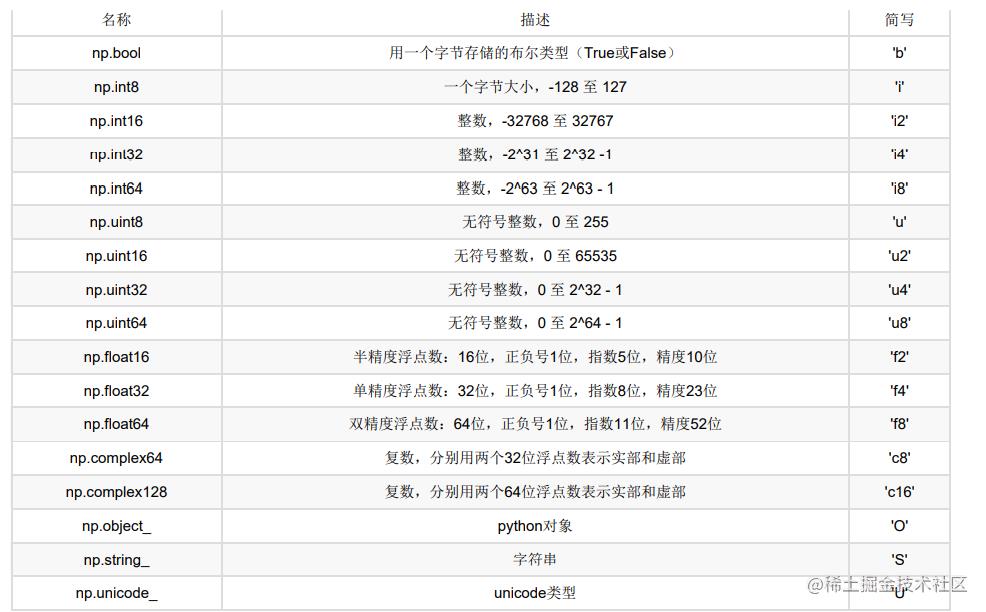
>>> a = np.array([[1, 2, 3],[4, 5, 6]], dtype=np.float32)

>>> a.dtype

dtype(‘float32’)

生成0,1数组

这个也是常用的，例如我们绘制一张图片。假设一张RGB图片，那么他是典型的（nxnx3）
nxn表示像素点。

ones = np.ones([4,8]) 
ones

array和asarray的不同

先说结论

Arrary相当于深度拷贝
asarrary 只是类型转换，相当于浅拷贝

创建等差数组

指定步长参数
- step:步长,默认值为1
  np.arange(10, 50, 2)

创建正态分布

np.random.normal(loc=0.0, scale=1.0, size=None)

loc：float
此概率分布的均值（对应着整个分布的中心centre）
scale：float 此概率分布的标准差（对应于分布的宽度，scale越大越矮胖，scale越小，越瘦高）
size：int or tuple of ints 输出的shape，默认为None，只输出一个值
np.random.standard_normal(size=None) 返回指定形状的标准正态分布的数组。

形状修改

np.reshape(shape)

元素的Curd

这个的api的模板固定，只是api名称不同。我们这边演示添加

import numpy as np
#创建数组arr arr = np.array([[1,2,3,4],[5,6,7,8]]) 
print('第1个数组arr：',arr)　　 
print('向arr数组添加元素：') 
print(np.append(arr,[[9,10],[11,12]])) 
print('原数组：',arr)　　 
print('沿轴 0 添加元素：') 
print(np.append(arr,[[9,10,11,12],[11,11,11,11]], axis=0)) 
print('沿轴 1 添加元素：') 
print(np.append(arr,[[9,10],[11,12]], axis=1))

注意接受参数

运算

逻辑运算

# 生成10名同学，5门功课的数据
>>> score = np.random.randint(40, 100, (10, 5))
# 取出最后4名同学的成绩，用于逻辑判断
>>> test_score = score[6:, 0:5]
# 逻辑判断, 如果成绩大于60就标记为True 否则为False
>>> test_score > 60
array([[ True, True, True, False, True],
[ True, True, True, False, True],
[ True, True, False, False, True],
[False, True, True, True, True]])
# BOOL赋值, 将满足条件的设置为指定的值-布尔索引
>>> test_score[test_score > 60] = 1
>>> test_score
array([[ 1, 1, 1, 52, 1],
[ 1, 1, 1, 59, 1],
[ 1, 1, 44, 44, 1],
[59, 1, 1, 1, 1]])

三元运算

np.where(temp > 60, 1, 0)

矩阵运算

广播机制

arr1 = np.array([[0],[1],[2],[3]])
arr1.shape
# (4, 1)
arr2 = np.array([1,2,3])
arr2.shape
# (3,)
arr1+arr2
# 结果是：
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 5],
[4, 5, 6]])