我画了25张图展示线程池工作原理和实现原理,原创干货,建议先收藏再阅读
Posted JavaQ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了我画了25张图展示线程池工作原理和实现原理,原创干货,建议先收藏再阅读相关的知识,希望对你有一定的参考价值。
好记性不如烂笔头,记录下来的才是永恒!这里是JavaQ大本营,诚邀关注。
上篇《这样的API网关查询接口优化,我是被迫的》文章末尾,有朋友留言提到文中的场景是IO密集型操作,不是CPU密集操作,不需要使用线程池,我猜这位朋友可能想表达的是IO密集且阻塞时间久的不要使用线程池方案解决。IO密集型在控制好同步处理时间或阻塞等待的条件下是可以使用线程池的,不知道这么描述是否合理,有高见的大佬可以继续留言讨论。
关注过我更新频率的朋友会发现有好几天没有上新内容了,原因有二,一是最近真的太忙了,项目催的紧,程序员哪有不加班是吧;另一个是我正在梳理技能图谱,后续的内容更新会根据这个图谱来,还在进行中,有兴趣的朋友持续关注下我和我的github:https://github.com/wind7rui/JavaHub,持续更新哦!好了,开始我们今天的话题~线程池。注意:下方多图高能预警,建议先收藏后阅读,防止走丢!
为什么要使用线程池平时讨论多线程处理,大佬们必定会说使用线程池,那为什么要使用线程池?其实,这个问题可以反过来思考一下,不使用线程池会怎么样?当需要多线程并发执行任务时,只能不断的通过new Thread创建线程,每创建一个线程都需要在堆上分配内存空间,同时需要分配虚拟机栈、本地方法栈、程序计数器等线程私有的内存空间,当这个线程对象被可达性分析算法标记为不可用时被GC回收,这样频繁的创建和回收需要大量的额外开销。再者说,JVM的内存资源是有限的,如果系统中大量的创建线程对象,JVM很可能直接抛出OutOfMemoryError异常,还有大量的线程去竞争CPU会产生其他的性能开销,更多的线程反而会降低性能,所以必须要限制线程数。
既然不使用线程池有那么多问题,我们来看一下使用线程池有哪些好处:
使用线程池可以复用池中的线程,不需要每次都创建新线程,减少创建和销毁线程的开销;
同时,线程池具有队列缓冲策略、拒绝机制和动态管理线程个数,特定的线程池还具有定时执行、周期执行功能,比较重要的一点是线程池可实现线程环境的隔离,例如分别定义支付功能相关线程池和优惠券功能相关线程池,当其中一个运行有问题时不会影响另一个。
本文内容我们只聊线程池ThreadPoolExecutor,查看它的源码会发现它继承了AbstractExecutorService抽象类,而AbstractExecutorService实现了ExecutorService接口,ExecutorService继承了Executor接口,所以ThreadPoolExecutor间接实现了ExecutorService接口和Executor接口,它们的关系图如下。
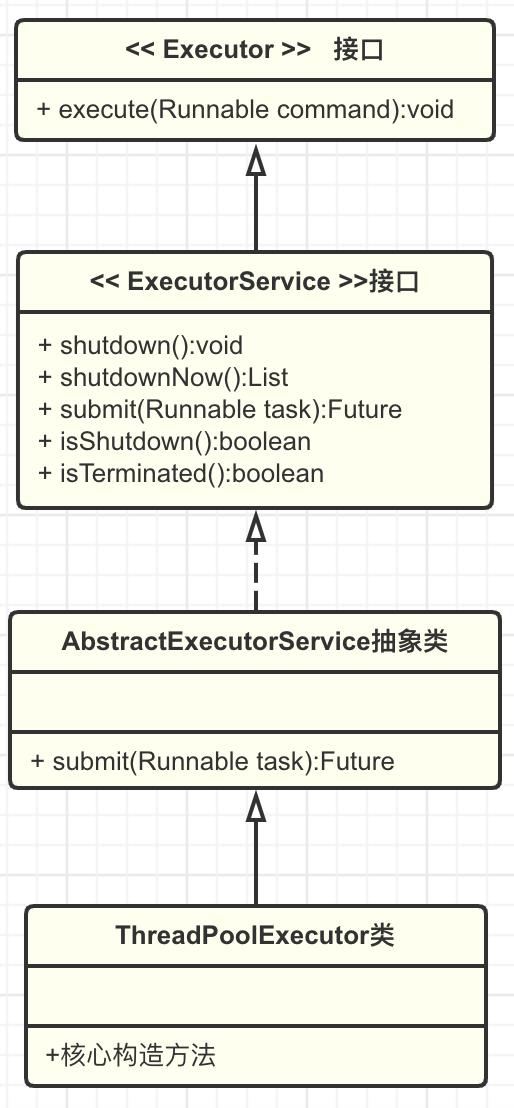
一般我们使用的execute方法是在Executor接口中定义的,而submit方法是在ExecutorService接口中定义的,所以当我们创建一个Executor类型变量引用ThreadPoolExecutor对象实例时可以使用execute方法提交任务,当我们创建一个ExecutorService类型变量时可以使用submit方法,当然我们可以直接创建ThreadPoolExecutor类型变量使用execute方法或submit方法。
ThreadPoolExecutor定义了七大核心属性,这些属性是线程池实现的基石。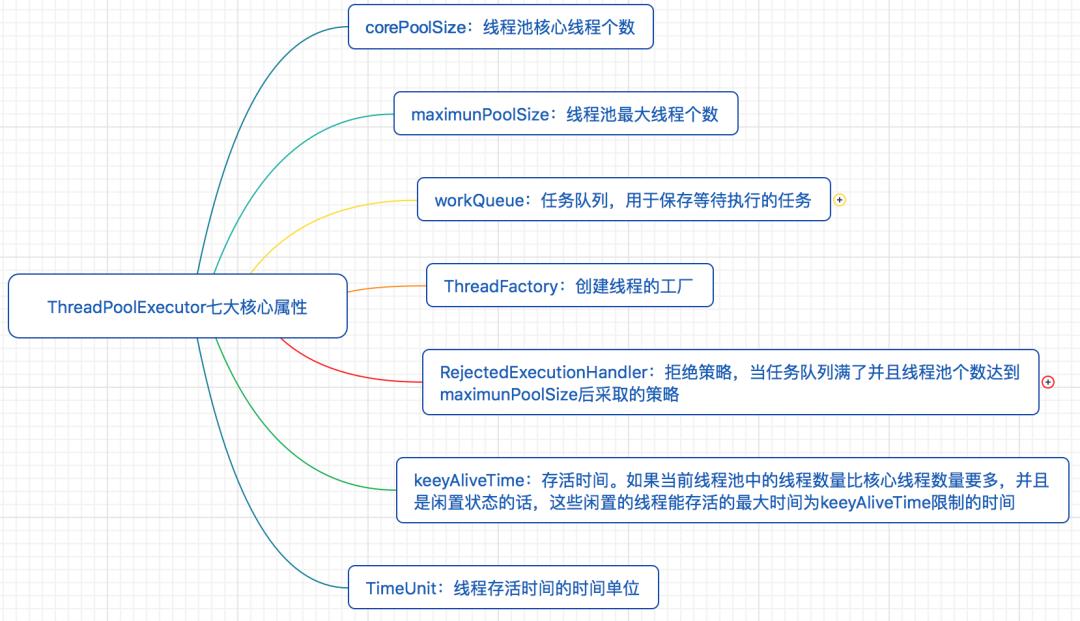
corePoolSize(int):核心线程数量。默认情况下,在创建了线程池后,线程池中的线程数为0,当有任务来之后,就会创建一个线程去执行任务,当线程池中的线程数目达到corePoolSize后,就会把到达的任务放到任务队列当中。线程池将长期保证这些线程处于存活状态,即使线程已经处于闲置状态。除非配置了allowCoreThreadTimeOut=true,核心线程数的线程也将不再保证长期存活于线程池内,在空闲时间超过keepAliveTime后被销毁。
workQueue:阻塞队列,存放等待执行的任务,线程从workQueue中取任务,若无任务将阻塞等待。当线程池中线程数量达到corePoolSize后,就会把新任务放到该队列当中。JDK提供了四个可直接使用的队列实现,分别是:基于数组的有界队列ArrayBlockingQueue、基于链表的无界队列LinkedBlockingQueue、只有一个元素的同步队列SynchronousQueue、优先级队列PriorityBlockingQueue。在实际使用时一定要设置队列长度。
maximumPoolSize(int):线程池内的最大线程数量,线程池内维护的线程不得超过该数量,大于核心线程数量小于最大线程数量的线程将在空闲时间超过keepAliveTime后被销毁。当阻塞队列存满后,将会创建新线程执行任务,线程的数量不会大于maximumPoolSize。
keepAliveTime(long):线程存活时间,若线程数超过了corePoolSize,线程闲置时间超过了存活时间,该线程将被销毁。除非配置了allowCoreThreadTimeOut=true,核心线程数的线程也将不再保证长期存活于线程池内,在空闲时间超过keepAliveTime后被销毁。
TimeUnit unit:线程存活时间的单位,例如TimeUnit.SECONDS表示秒。
RejectedExecutionHandler:拒绝策略,当任务队列存满并且线程池个数达到maximunPoolSize后采取的策略。ThreadPoolExecutor中提供了四种拒绝策略,分别是:抛RejectedExecutionException异常的AbortPolicy(如果不指定的默认策略)、使用调用者所在线程来运行任务CallerRunsPolicy、丢弃一个等待执行的任务,然后尝试执行当前任务DiscardOldestPolicy、不动声色的丢弃并且不抛异常DiscardPolicy。项目中如果为了更多的用户体验,可以自定义拒绝策略。
threadFactory:创建线程的工厂,虽说JDK提供了线程工厂的默认实现DefaultThreadFactory,但还是建议自定义实现最好,这样可以自定义线程创建的过程,例如线程分组、自定义线程名称等。
一般我们使用类的构造方法创建它的对象,ThreadPoolExecutor提供了四个构造方法。
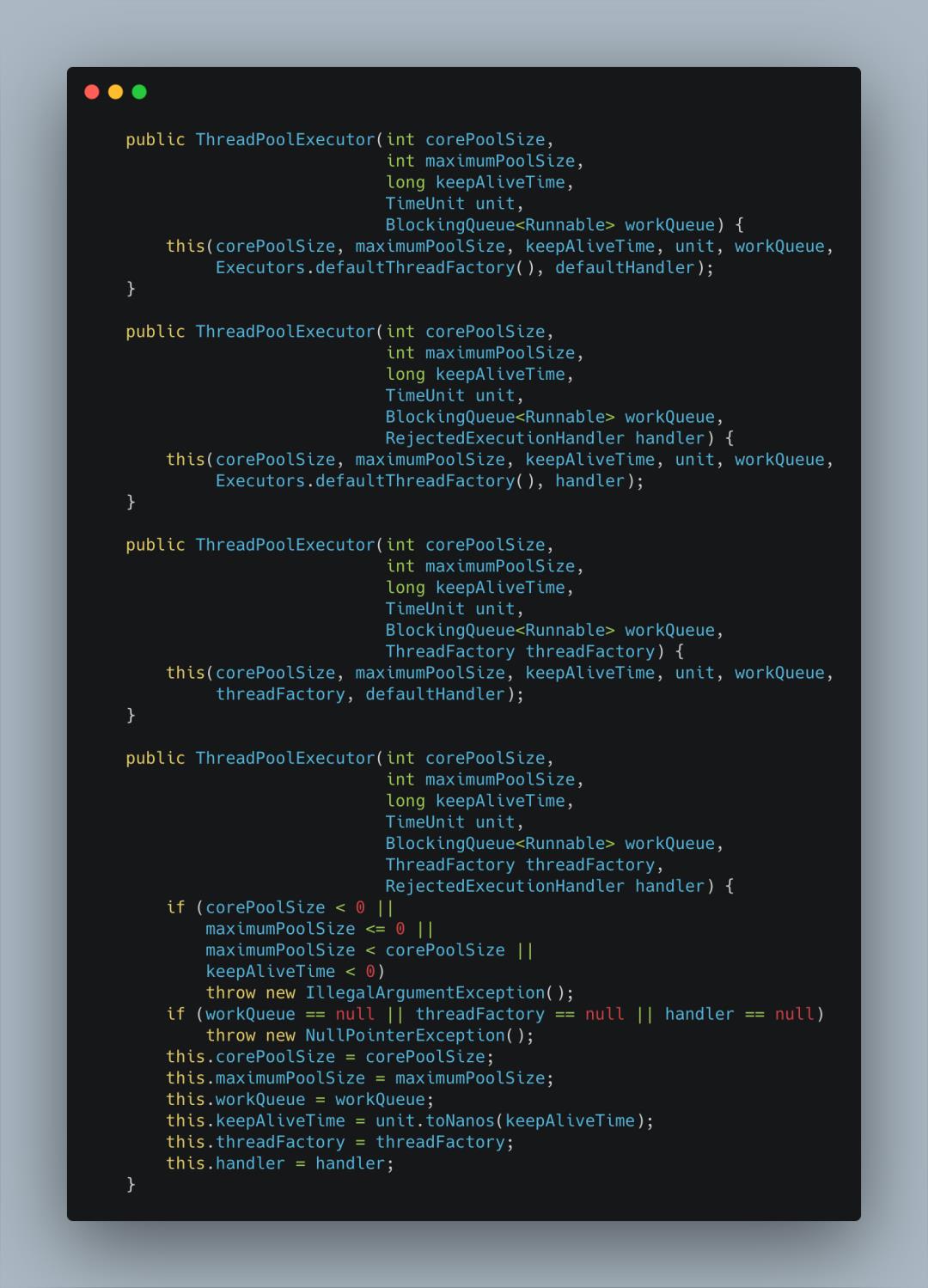
可以看到前三个方法最终都调用了最后一个、参数列表最长的那个方法,在这个方法中给七个属性赋值。创建线程池对象,强烈建议通过使用ThreadPoolExecutor的构造方法创建,不要使用Executors,至于建议的理由上文中也有说过,这里再引用阿里《Java开发手册》中的一段描述。

了解了线程池ThreadPoolExecutor的基本构造,接下来手撸一段代码看看如何使用,样例代码中的参数仅为了配合原理解说使用。
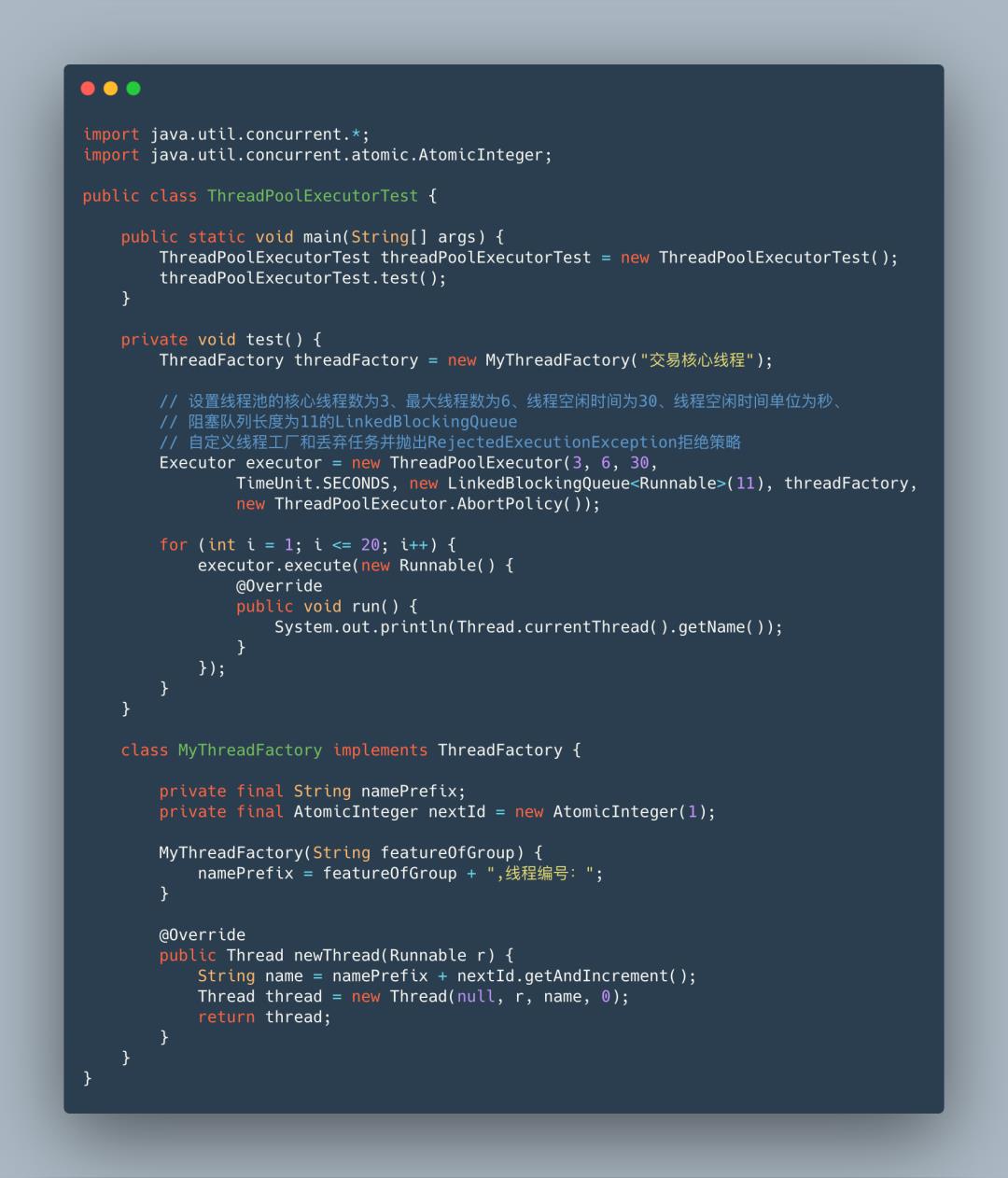
关于线程池的工作原理,我用下面的7幅图来展示。
1.通过execute方法提交任务时,当线程池中的线程数小于corePoolSize时,新提交的任务将通过创建一个新线程来执行,即使此时线程池中存在空闲线程。
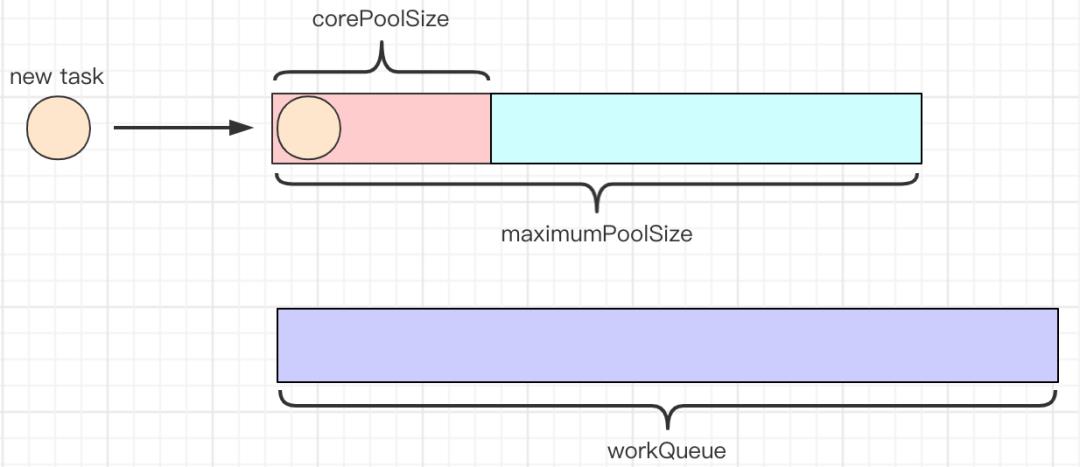
2.通过execute方法提交任务时,当线程池中线程数量达到corePoolSize时,新提交的任务将被放入workQueue中,等待线程池中线程调度执行。
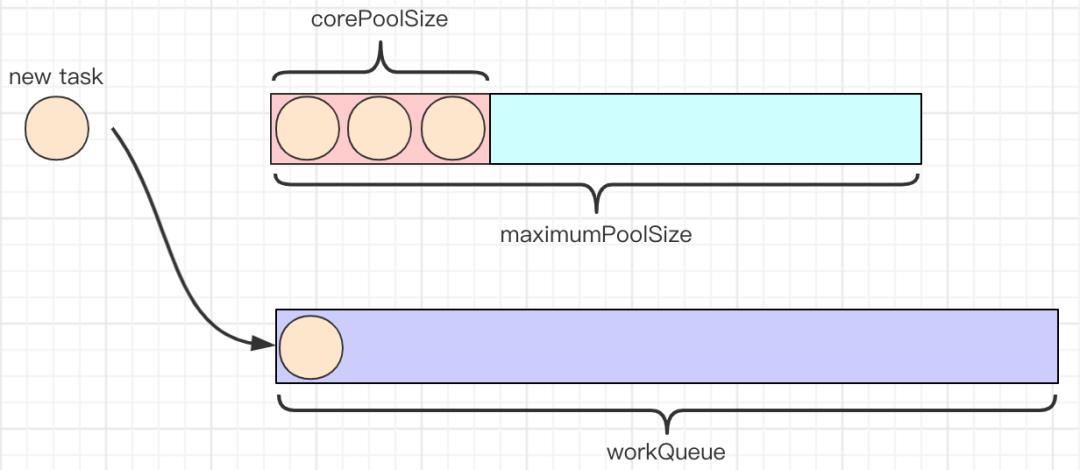
3.通过execute方法提交任务时,当workQueue已存满,且maximumPoolSize大于corePoolSize时,新提交的任务将通过创建新线程执行。
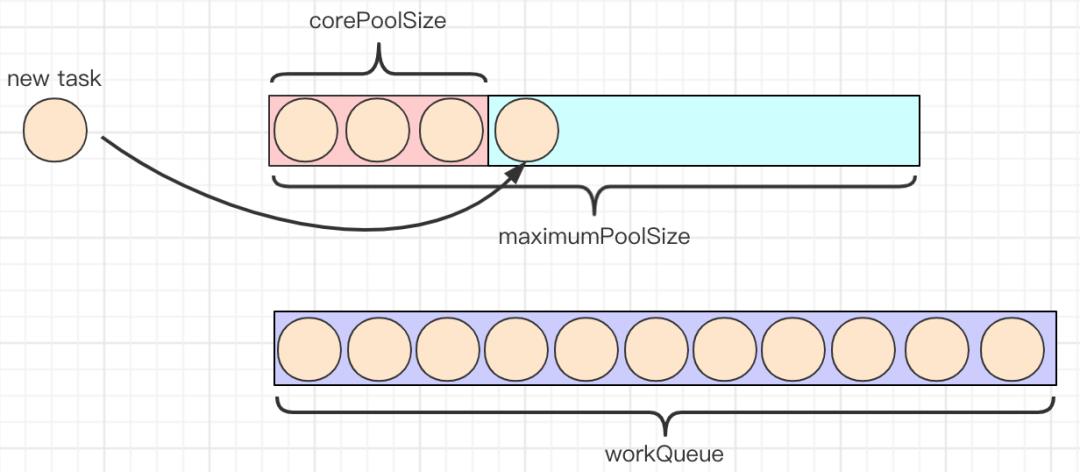
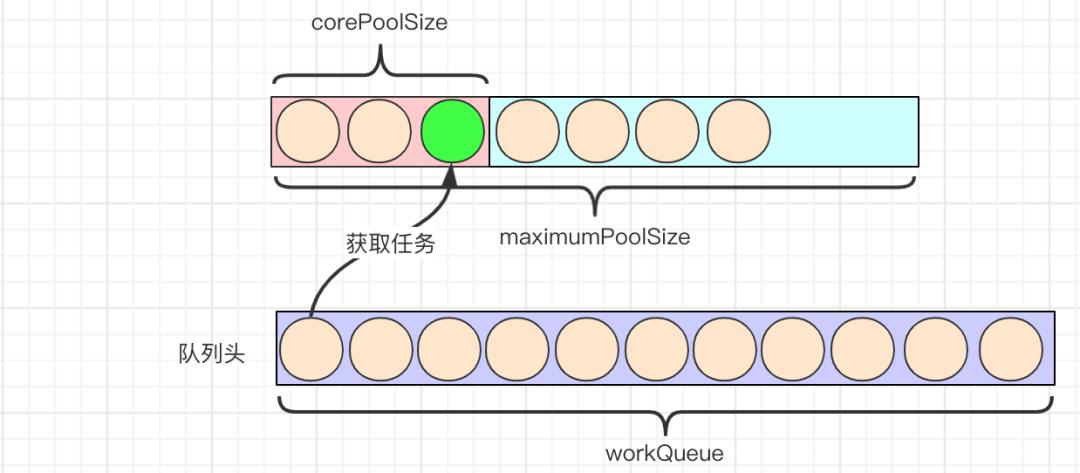
4.当线程池中的线程执行完任务空闲时,会尝试从workQueue中取头结点任务执行。
5.通过execute方法提交任务,当线程池中线程数达到maxmumPoolSize,并且workQueue也存满时,新提交的任务由RejectedExecutionHandler执行拒绝操作。
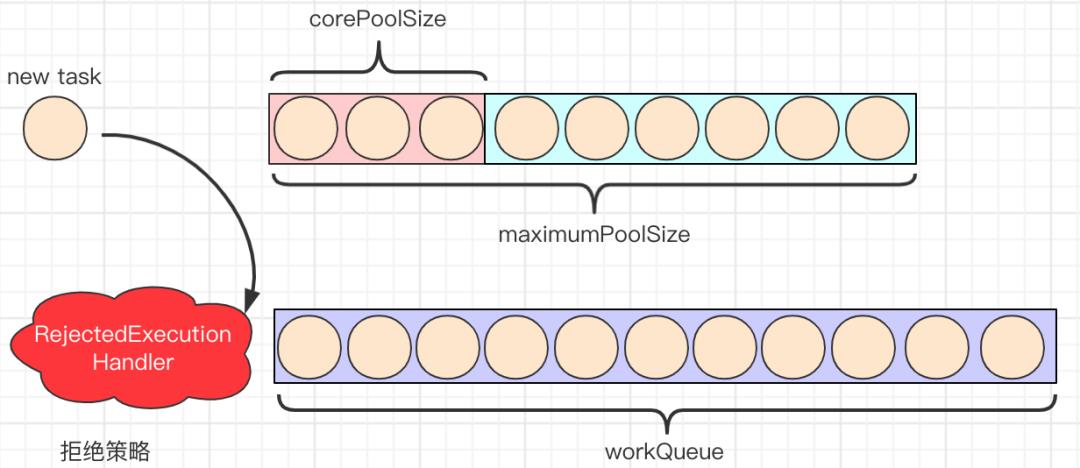
6.当线程池中线程数超过corePoolSize,并且未配置allowCoreThreadTimeOut=true,空闲时间超过keepAliveTime的线程会被销毁,保持线程池中线程数为corePoolSize。
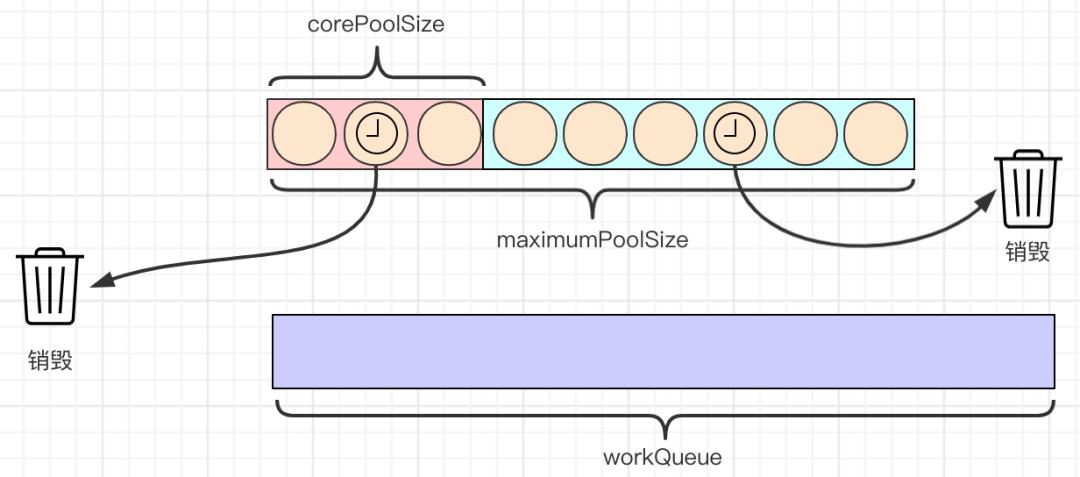
注意:上图表达的是销毁空闲线程,保持线程数为corePoolSize,不是销毁corePoolSize中的线程。
7.当设置allowCoreThreadTimeOut=true时,任何空闲时间超过keepAliveTime的线程都会被销毁。
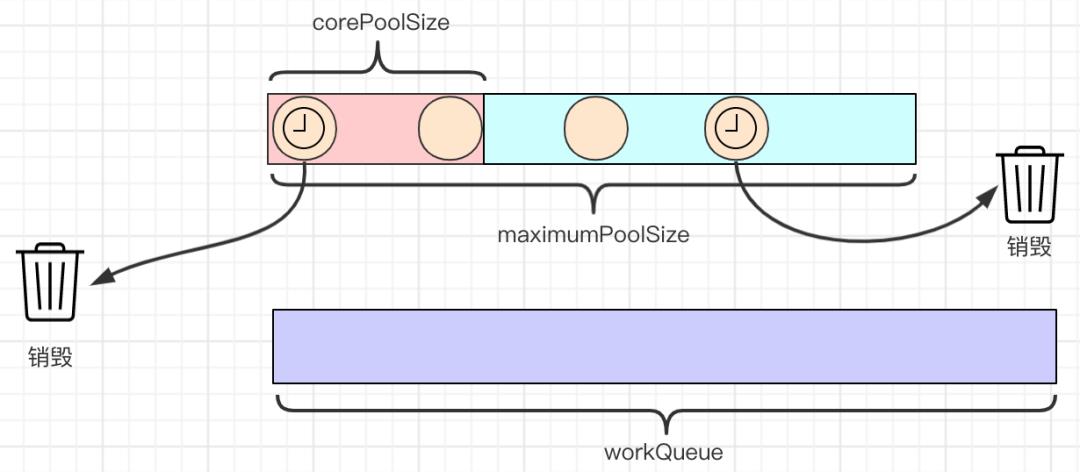
查看ThreadPoolExecutor的源码,发现ThreadPoolExecutor的实现还是比较复杂的,下面简单介绍几个重要的全局常量和方法。
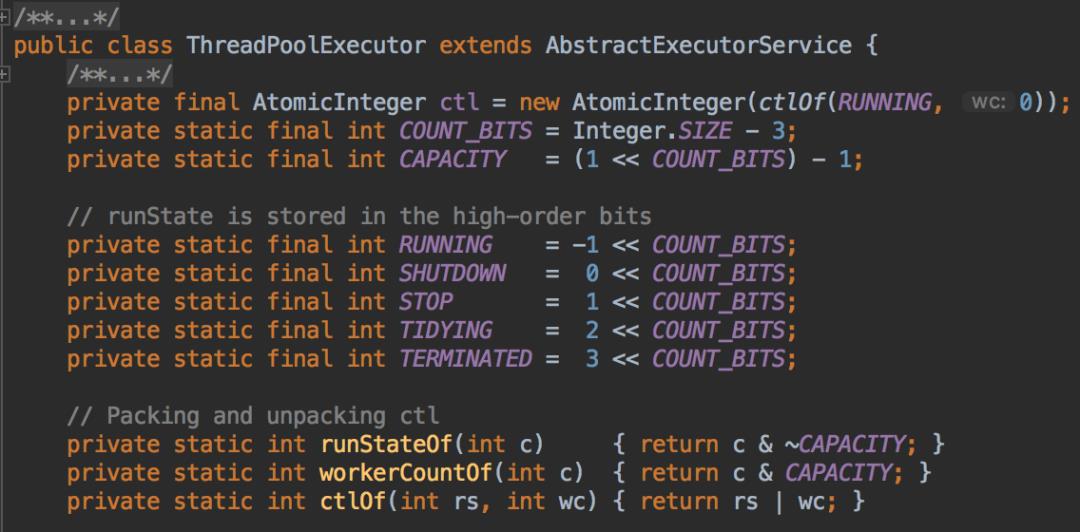
ctl用于表示线程池的状态和线程数,在ThreadPoolExecutor中使用32位二进制数来表示线程池的状态和线程池中线程数量,其中前3位表示线程池状态,后29位表示线程池中线程数。private final AtomicInteger ctl = new AtomicInteger(ctlOf(RUNNING, 0))初始化线程池状态为RUNNING、线程池数量为0。

COUNT_BITS值等于Integer.SIZE - 3,在源码中Integer.SIZE是32,所以COUNT_BITS=29。CAPACITY表示线程池允许的最大线程数,转算后的结果如下。

RUNNING、SHUTDOWN、STOP、TIDYING和TERMINATED分别表示线程池的不同状态,转算后的结果如下。
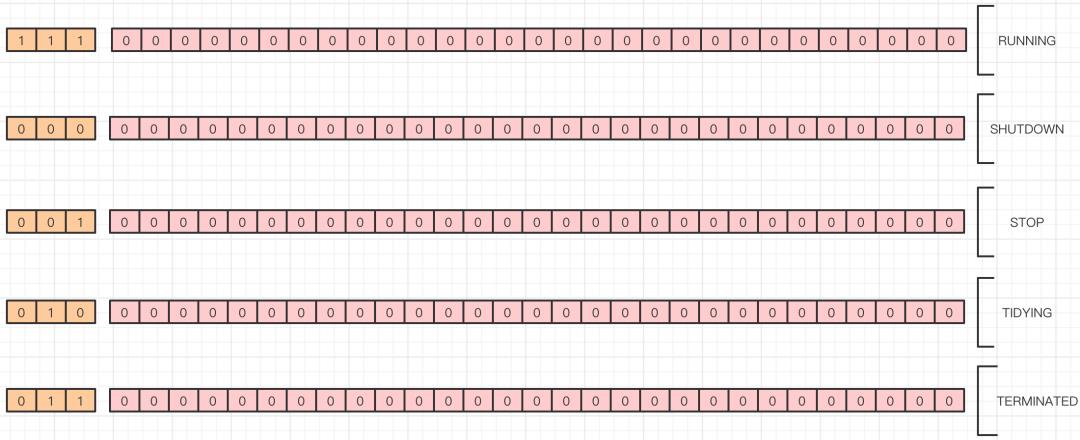
线程池处在不同的状态时,它的处理能力是不同的。
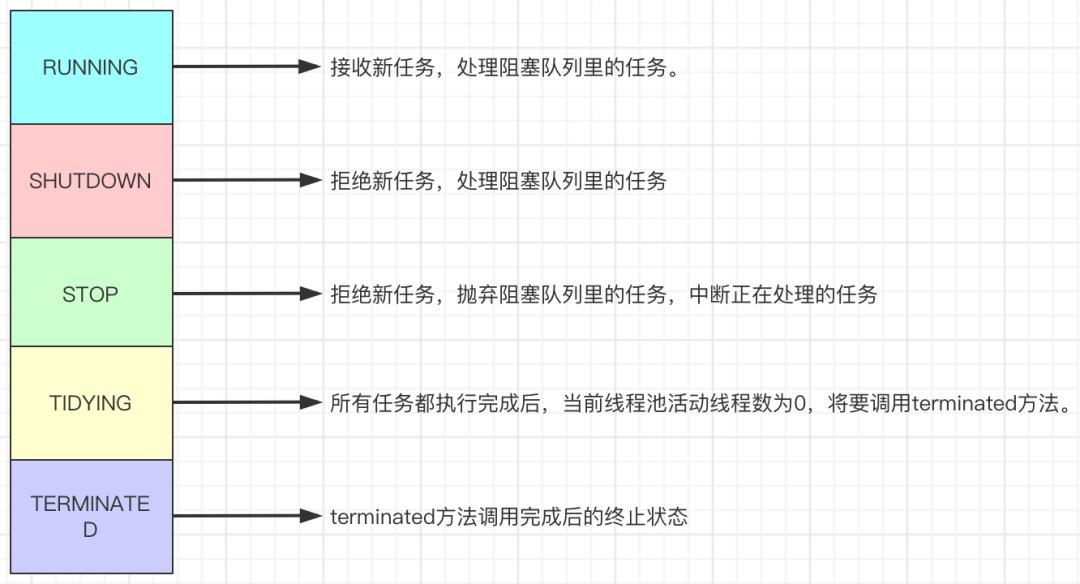
线程池不同状态之间的转换时机及转换关系如下图。
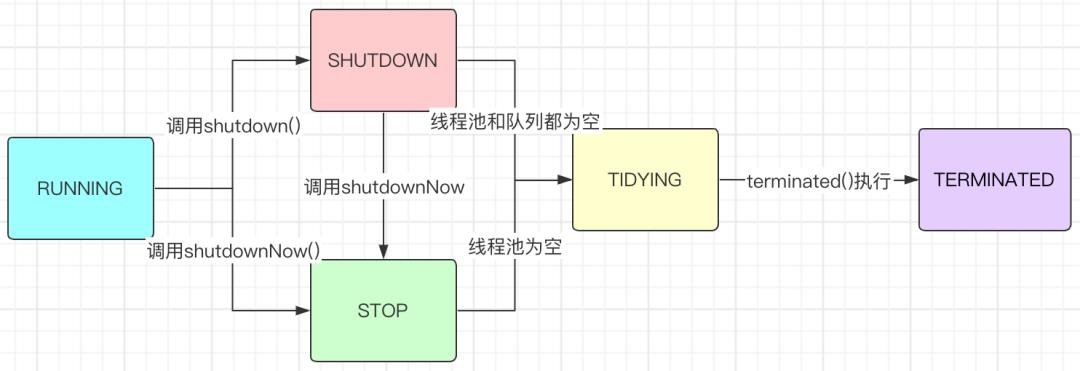
runStateOf获取ctl高三位,也就是线程池的状态。workerCountOf获取ctl低29位,也就是线程池中线程数。ctlOf计算ctlOf新值,也就是线程池状态和线程池个数。
你可能会疑问“为什么要介绍上面这些?”,这是因为接下来的源码分析会用到这些基础的知识点。一般,我们使用ThreadPoolExecutor的execute方法提交任务,所以从execute的源码入手。
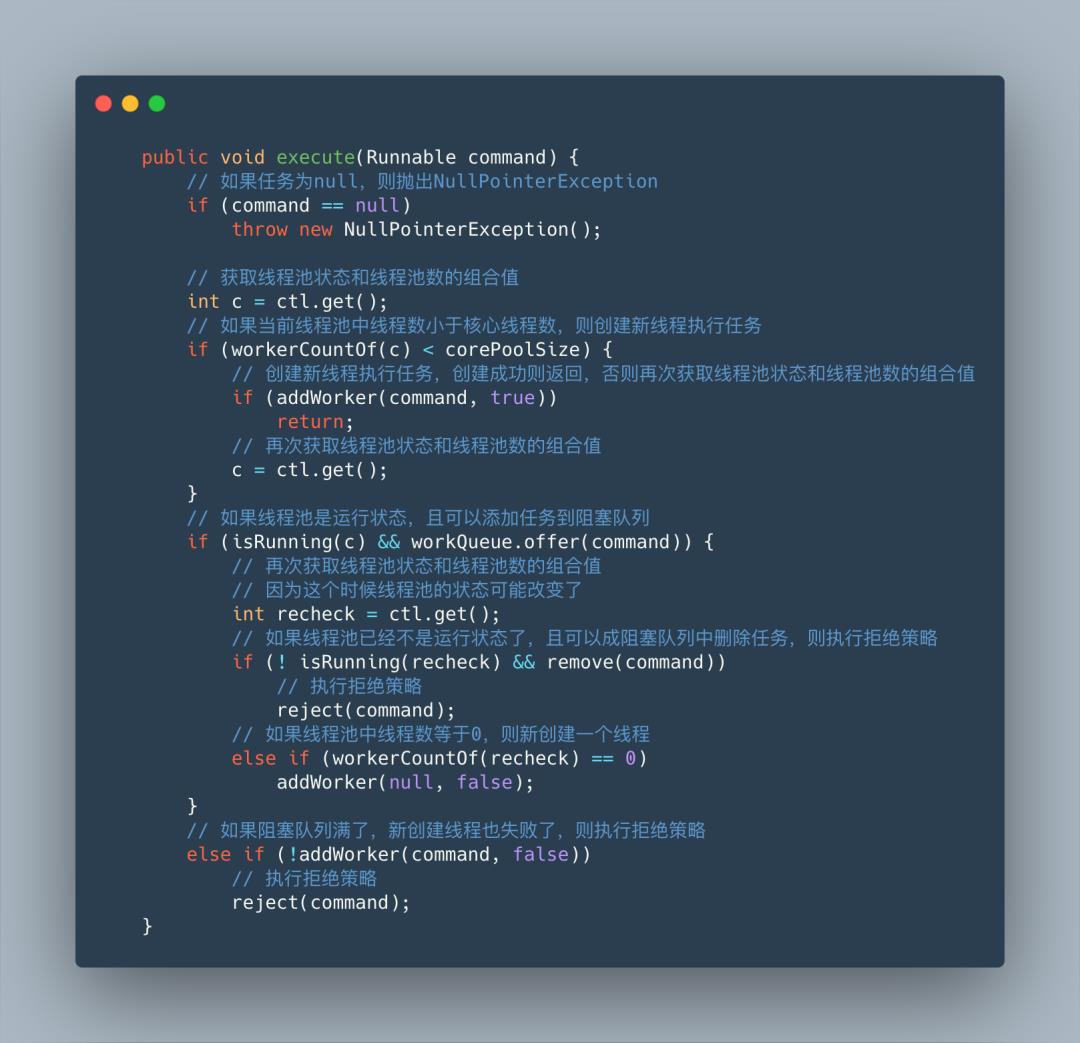
为了更轻松的理解上图中的源码,我又画了一个流程图。
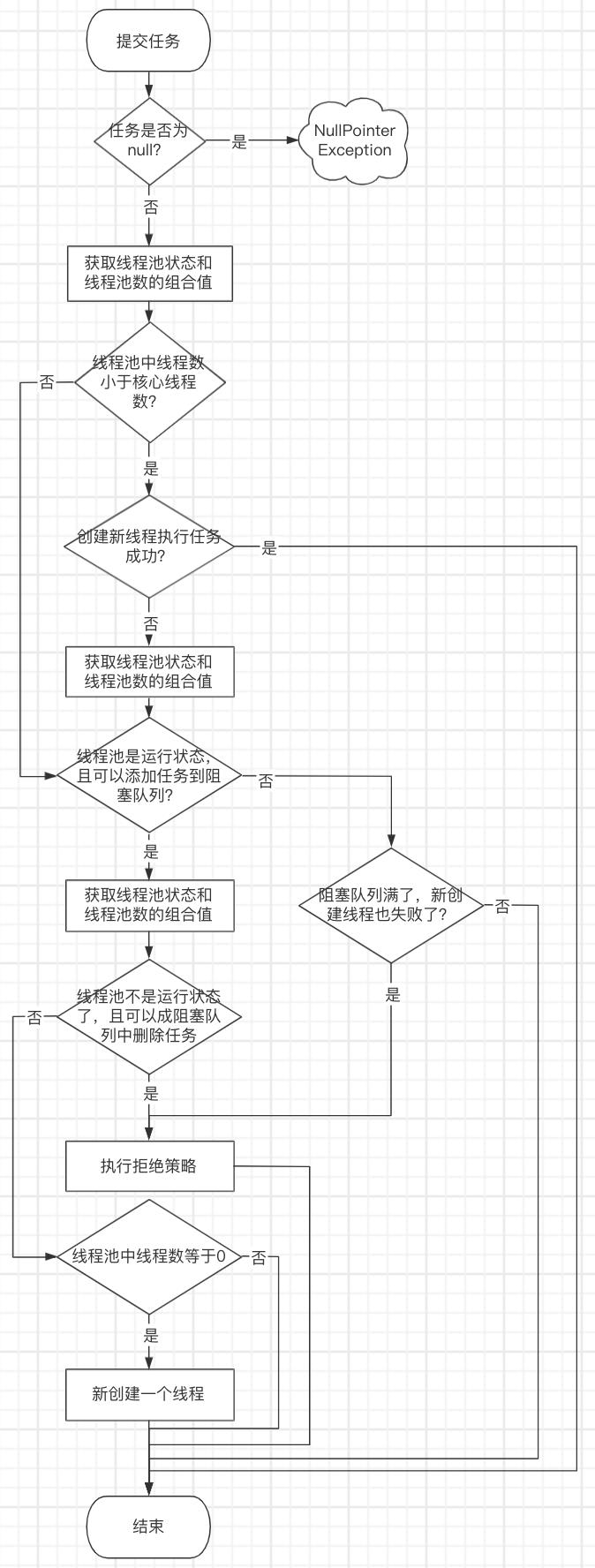
到这里线程池的基本实现原理已经很清晰了,接下来我们重点分析一下线程池中线程是如何执行任务、如何复用线程和线程空闲时间超限如何判断的。还是从execute方法入手,我们直接看它里面调用的addWorker方法,它实现了创建新线程执行任务。
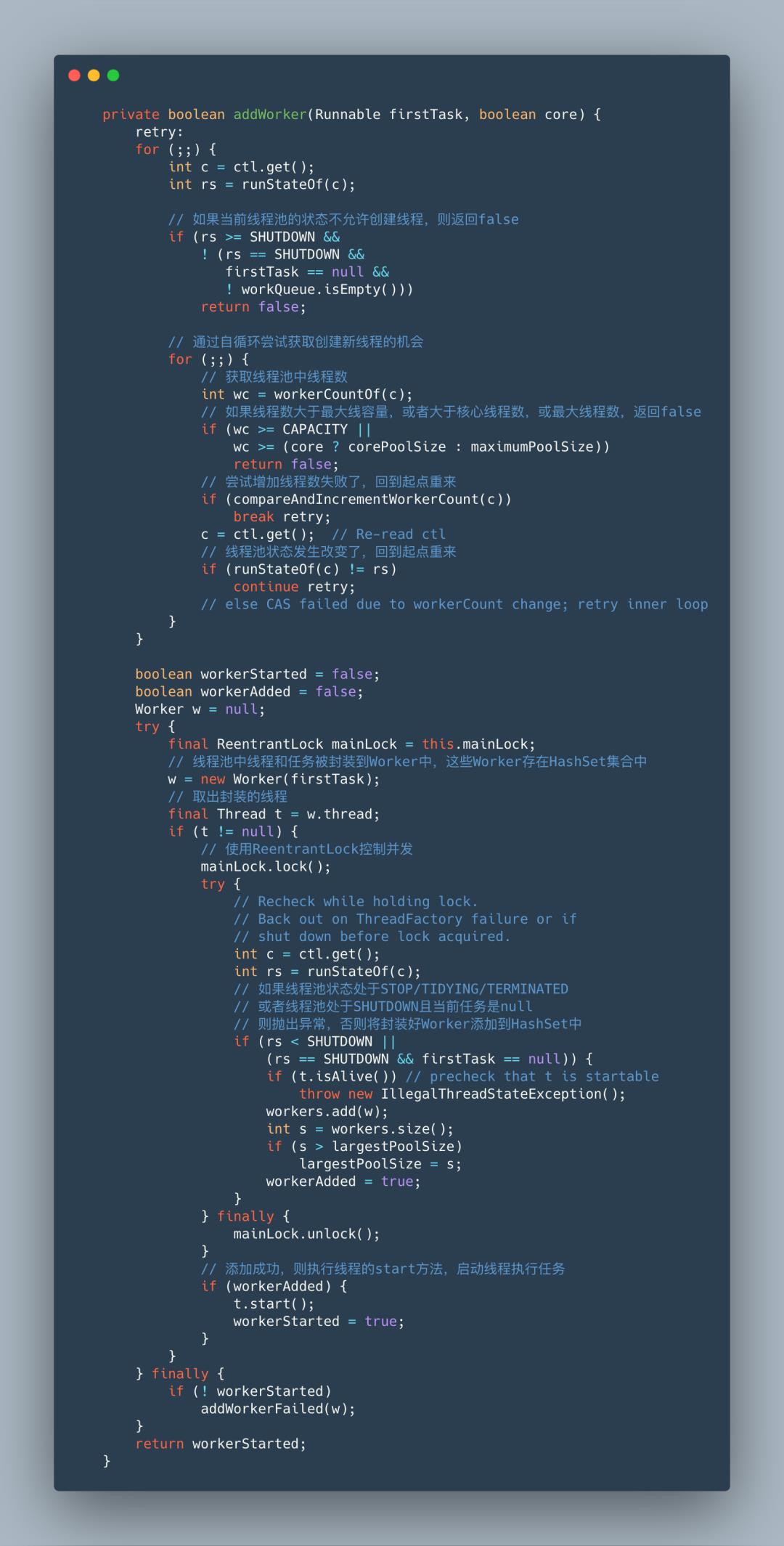
源码中将线程和任务封装到了Worker中,然后将Worker添加到HashSet集合中,添加成功后通过线程对象的start方法启动线程执行任务,既然这样那我们就来看看上图代码中的w = new Worker(firstTask)到底是如何执行的。
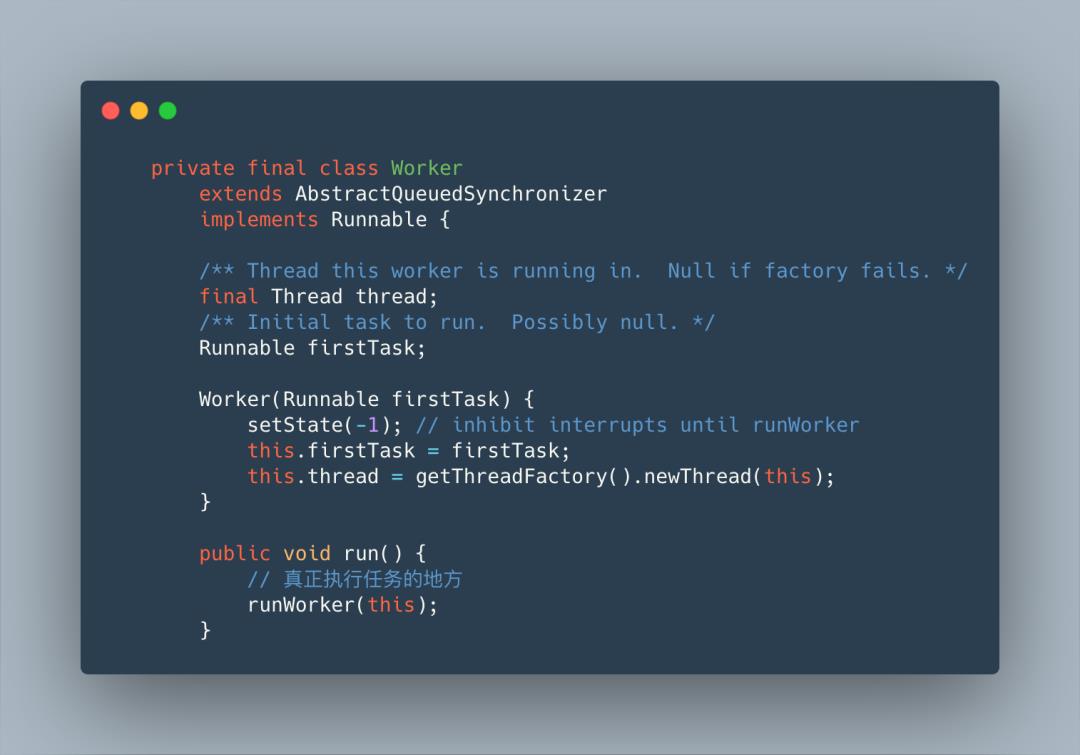
Worker继承了AbstractQueuedSynchronizer,并且实现了Runnable接口,看到这里很清楚了任务最终由Worker中的run方法执行,而run方法里调用了runWorker方法,所以重点还是runWorker方法。
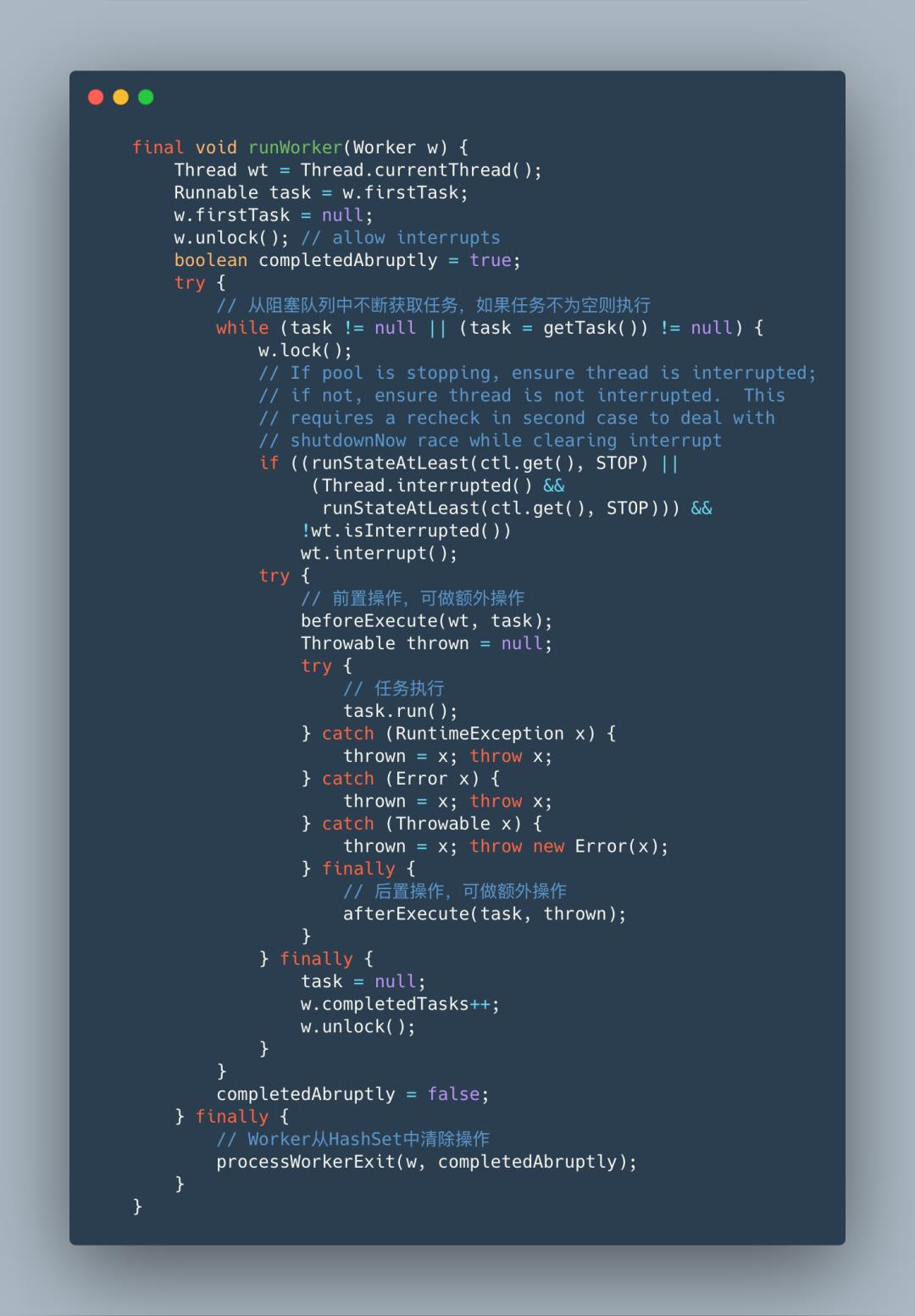
在runWorker方法中,使用循环,通过getTask方法,不断从阻塞队列中获取任务执行,如果任务不为空则执行任务,这里实现了线程的复用,不断的获取任务执行,不用重新创建线程;队列中获取的任务为null,则将Worker从HashSet集合中清除,注意这个清除就是空闲线程的回收。那getTask何时返回null?接着看getTask源码。
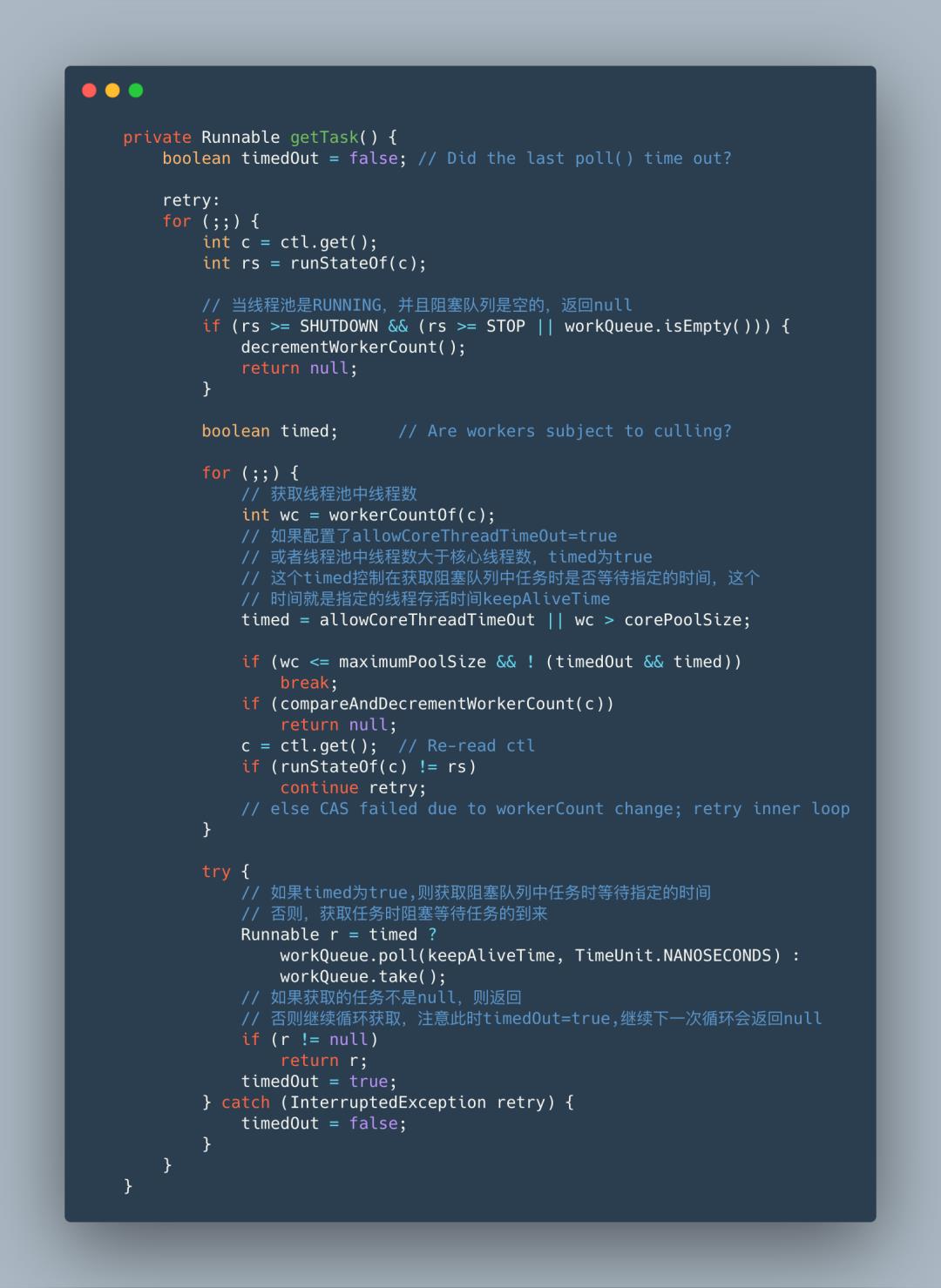
到这里,线程池中线程是如何执行任务、如何复用线程,以及线程空闲时间超限如何判断都已经清楚了。
最后,关于线程池的实现原理,我画了一张思维导图。ps:如果平台显示的不是高清图,可以在文末评论区或留言区@我,另外,本文全图文已收录到GitHub:https://github.com/wind7rui/JavaHub,后续其它内容也会更新到这里,欢迎follow、start。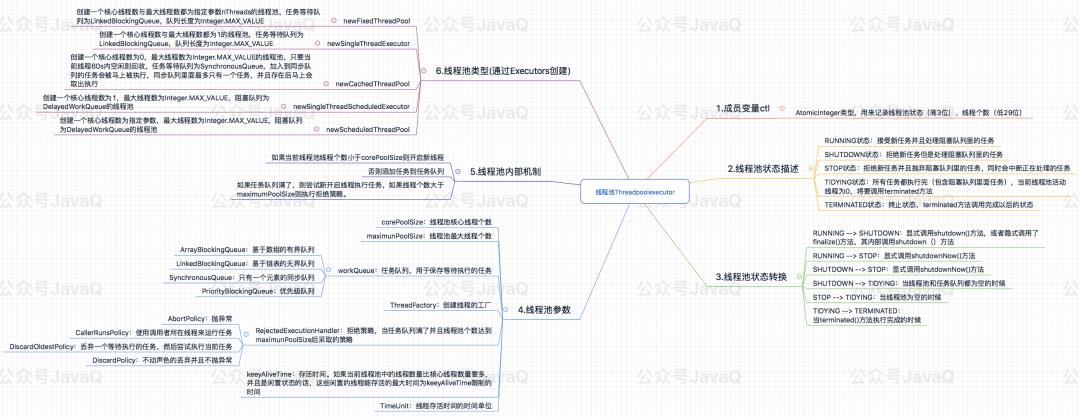
细心的朋友会发现,全文竟没有介绍Executors,这个创建线程池的辅助工具类。是的,我强烈不推荐使用它,因为Executors中的newFixedThreadPool和newSingleThreadExecutor方法创建的线程池中,阻塞队列LinkedBlockingQueue的长度是Integer.MAX_VALUE,可能会堆积大量的任务,从而导致 OOM;而newCachedThreadPool方法创建的线程池中最大线程数是Integer.MAX_VALUE,会创建大量的线程,从而导致OOM。如果创建线程池,通过ThreadPoolExecutor的构造方法创建,这样使用这个线程池的人会更加明确线程池的各个参数的设置及运行方式,提前避免隐藏问题的发生。
为什么要这么做呢?是因为,当项目规模逐渐扩展,各系统中线程池也不断增多,当发生线程执行问题时,通过自定义线程工厂创建的线程设置有意义的线程名称可快速追踪异常原因,高效、快速的定位问题。
使用自定义拒绝策略虽然,JDK给我们提供了一些默认的拒绝策略,但我们可以根据项目需求的需要,或者是用户体验的需要,定制拒绝策略,完成特殊需求。
不同业务、执行效率不同的分不同线程池,避免因某些异常导致整个线程池利用率下降或直接不可用,进而影响整个系统或其它系统的正常运行。
实际工作中,我们经常使用线程池,对这块的要求不仅是常规的如何使用,原理我们也要清楚是怎么回事。同时,线程池工作原理和底层实现原理也是面试必问的考题,所以,这块是一定要掌握的。
说实话,为了画这些图消耗了不少休息时间,如果你在看,点个赞支持一下我的原创吧!
学之多,而后知之少!朋友们点【在看】是我持续更新的最大动力,我们下期见!
我画了近百张图来理解红黑树
文章已同步发表于微信公众号JasonGaoH,我画了近百张图来理解红黑树,文章略有修改。
之前在公司组内分享了红黑树的工作原理,今天把它整理下发出来,希望能对大家有所帮助,对自己也算是一个知识点的总结。
这篇文章算是我写博客写公众号以来画图最多的一篇文章了,没有之一,我希望尽可能多地用图片来形象地描述红黑树的各种操作的前后变换原理,帮助大家来理解红黑树的工作原理,下面,多图预警开始了。
在讲红黑树之前,我们首先来了解下下面几个概念:二叉树,排序二叉树以及平衡二叉树。
二叉树
二叉树指的是每个节点最多只能有两个字数的有序树。通常左边的子树称为左子树 ,右边的子树称为右子树 。这里说的有序树强调的是二叉树的左子树和右子树的次序不能随意颠倒。
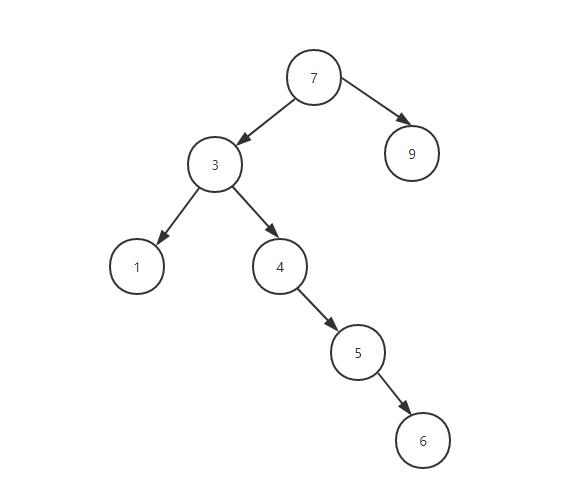
二叉树简单的示意图如下:

代码定义:
class Node
T data;
Node left;
Node right;
排序二叉树
所谓排序二叉树,顾名思义,排序二叉树是有顺序的,它是一种特殊结构的二叉树,我们可以对树中所有节点进行排序和检索。
性质
- 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若她的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 具有递归性,排序二叉树的左子树、右子树也是排序二叉树。
排序二叉树简单示意图:
排序二叉树退化成链表
排序二叉树的左子树上所有节点的值小于根节点的值,右子树上所有节点的值大于根节点的值,当我们插入一组元素正好是有序的时候,这时会让排序二叉树退化成链表。
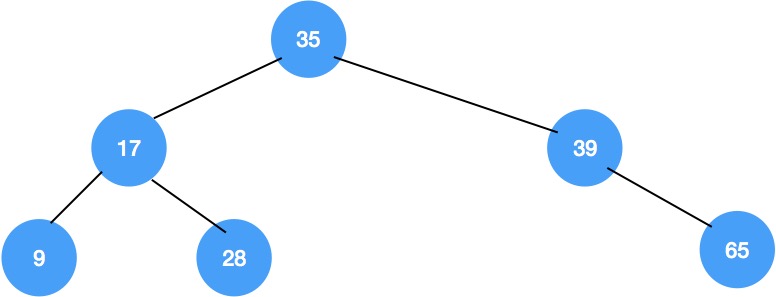
正常情况下,排序二叉树是如下图这样的:
但是,当插入的一组元素正好是有序的时候,排序二叉树就变成了下边这样了,就变成了普通的链表结构,如下图所示:
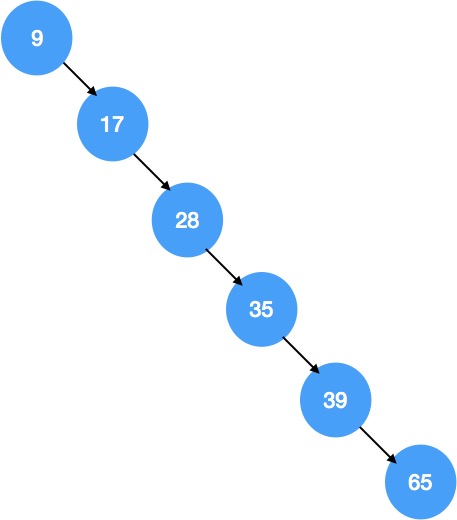
正常情况下的排序二叉树检索效率类似于二分查找,二分查找的时间复杂度为 O(log n),但是如果排序二叉树退化成链表结构,那么检索效率就变成了线性的 O(n) 的,这样相对于 O(log n) 来说,检索效率肯定是要差不少的。
思考,二分查找和正常的排序二叉树的时间复杂度都是 O(log n),那么为什么是O(log n) ?
关于 O(log n) 的分析下面这篇文章讲解的非常好,感兴趣的可以看下这篇文章 二分查找的时间复杂度,文章是拿二分查找来举例的,二分查找和平衡二叉树的时间复杂度是一样的,理解了二分查找的时间复杂度,再来理解平衡二叉树就不难了,这里就不赘述了。
继续回到我们的主题上,为了解决排序二叉树在特殊情况下会退化成链表的问题(链表的检索效率是 O(n) 相对正常二叉树来说要差不少),所以有人发明了平衡二叉树和红黑树类似的平衡树。
平衡二叉树
平衡二叉数又被称为 AVL 树,AVL 树的名字来源于它的发明作者 G.M. Adelson-Velsky 和 E.M. Landis,取自两人名字的首字母。
官方定义:它或者是一颗空树,或者具有以下性质的排序二叉树:它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
两个条件:
- 平衡二叉树必须是排序二叉树,也就是说平衡二叉树他的左子树所有节点的值必须小于根节点的值,它的右子树上所有节点的值必须大于它的根节点的值。
- 左子树和右子树的深度之差的绝对值不超过1。
红黑树
讲了这么多概念,接下来主角红黑树终于要上场了。
为什么有红黑树?
其实红黑树和上面的平衡二叉树类似,本质上都是为了解决排序二叉树在极端情况下退化成链表导致检索效率大大降低的问题,红黑树最早是由 Rudolf Bayer 于 1972 年发明的。
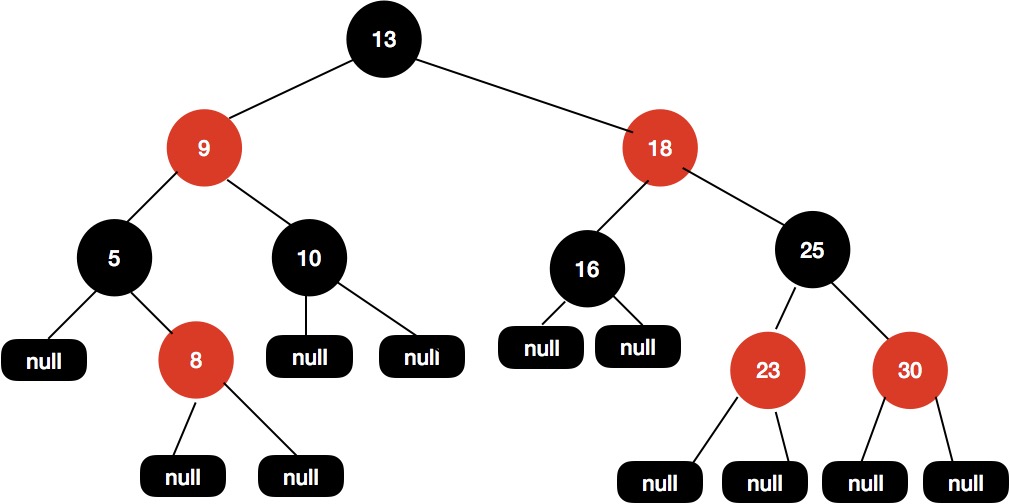
红黑树首先肯定是一个排序二叉树,它在每个节点上增加了一个存储位来表示节点的颜色,可以是 RED 或 BLACK 。
Java 中实现红黑树大概结构图如下所示:
红黑树的特性
- 性质1:每个节点要么是红色,要么是黑色。
- 性质2:根节点永远是黑色的。
- 性质3:所有的叶子节点都是空节点(即null),并且是黑色的。
- 性质4:每个红色节点的两个子节点都是黑色。(从每个叶子到根的路径上不会有两个连续的红色节点。)
- 性质5:从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
针对上面的 5 种性质,我们简单理解下,对于性质 1 和性质 2 ,相当于是对红黑树每个节点的约束,根节点是黑色,其他的节点要么是红色,要么是黑色。
对于性质 3 中指定红黑树的每个叶子节点都是空节点,而且叶子节点都是黑色,但 Java 实现的红黑树会使用 null 来代表空节点,因此我们在遍历 Java里的红黑树的时候会看不到叶子节点,而看到的是每个叶子节点都是红色的,这一点需要注意。
对于性质 5,这里我们需要注意的是,这里的描述是从任一节点,从任一节点到它的子树的每个叶子节点黑色节点的数量都是相同的,这个数量被称为这个节点的黑高。
如果我们从根节点出发到每个叶子节点的路径都包含相同数量的黑色节点,这个黑色节点的数量被称为树的黑色高度。树的黑色高度和节点的黑色高度是不一样的,这里要注意区分。
其实到这里有人可能会问了,红黑树的性质说了一大堆,那是不是说只要保证红黑树的节点是红黑交替就能保证树是平衡的呢?
其实不是这样的,我们可以看来看下面这张图:
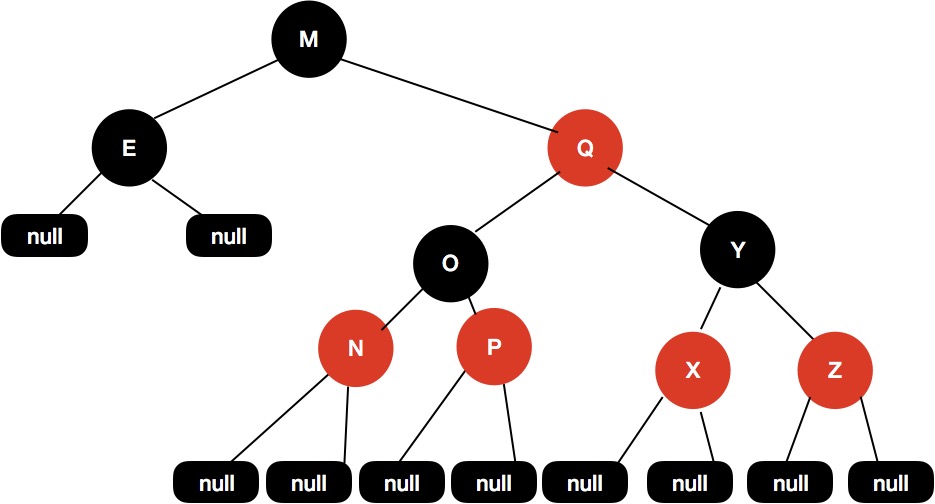
左边的子树都是黑色节点,但是这个红黑树依然是平衡的,5 条性质它都满足。
这个树的黑色高度为 3,从根节点到叶子节点的最短路径长度是 2,该路径上全是黑色节点,包括叶子节点,从根节点到叶子节点最长路径为 4,每个黑色节点之间会插入红色节点。
通过上面的性质 4 和性质 5,其实上保证了没有任何一条路径会比其他路径长出两倍,所以这样的红黑树是平衡的。
其实这算是一个推论,红黑树在最差情况下,最长的路径都不会比最短的路径长出两倍。其实红黑树并不是真正的平衡二叉树,它只能保证大致是平衡的,因为红黑树的高度不会无限增高,在实际应用用,红黑树的统计性能要高于平衡二叉树,但极端性能略差。
红黑树的插入
想要彻底理解红黑树,除了上面说到的理解红黑树的性质以外,就是理解红黑树的插入操作了。
红黑树的插入和普通排序二叉树的插入基本一致,排序二叉树的要求是左子树上的所有节点都要比根节点小,右子树上的所有节点都要比跟节点大,当插入一个新的节点的时候,首先要找到当前要插入的节点适合放在排序二叉树哪个位置,然后插入当前节点即可。红黑树和排序二叉树不同的是,红黑树需要在插入节点调整树的结构来让树保持平衡。
一般情况下,红黑树中新插入的节点都是红色的,那么,为什么说新加入到红黑树中的节点要是红色的呢?
这个问题可以这样理解,我们从性质5中知道,当前红黑树中从根节点到每个叶子节点的黑色节点数量是一样的,此时假如新的黑色节点的话,必然破坏规则,但加入红色节点却不一定,除非其父节点就是红色节点,因此加入红色节点,破坏规则的可能性小一些。
接下来我们重点来讲红黑树插入新节点后是如何保持平衡的。
给定下面这样一颗红黑树:
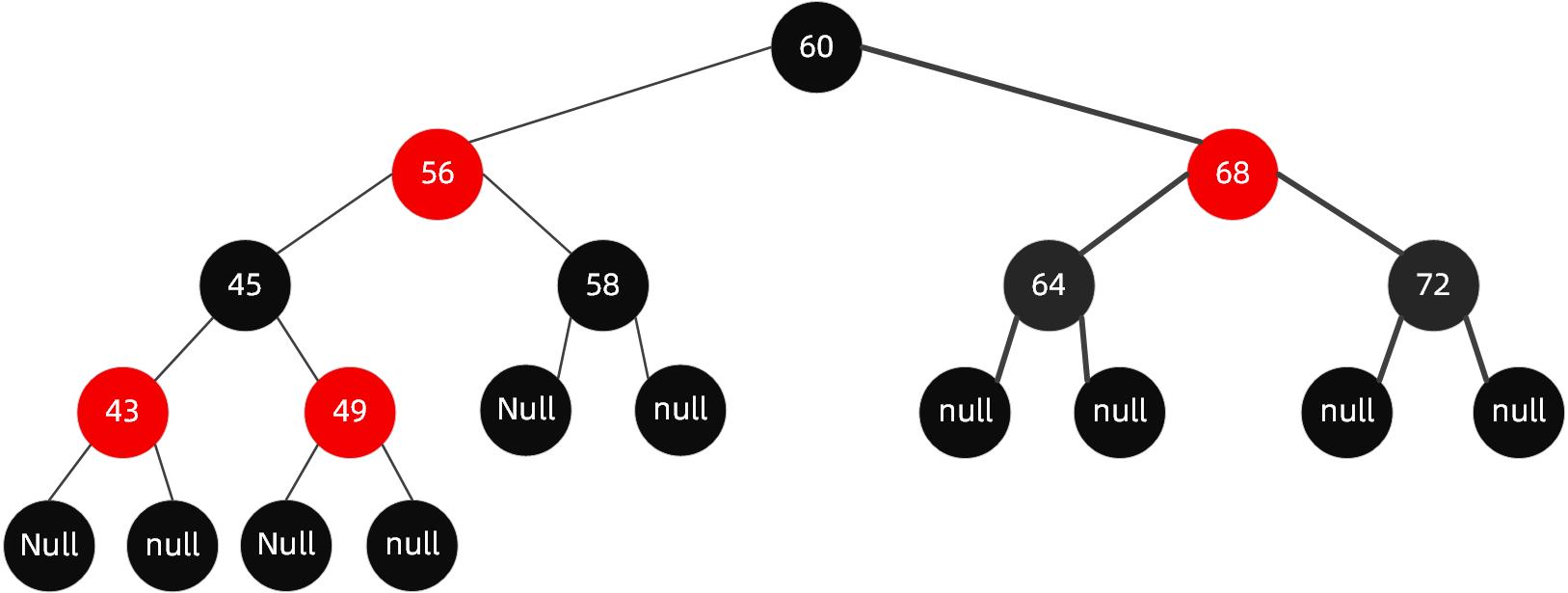
当我们插入值为66的节点的时候,示意图如下:
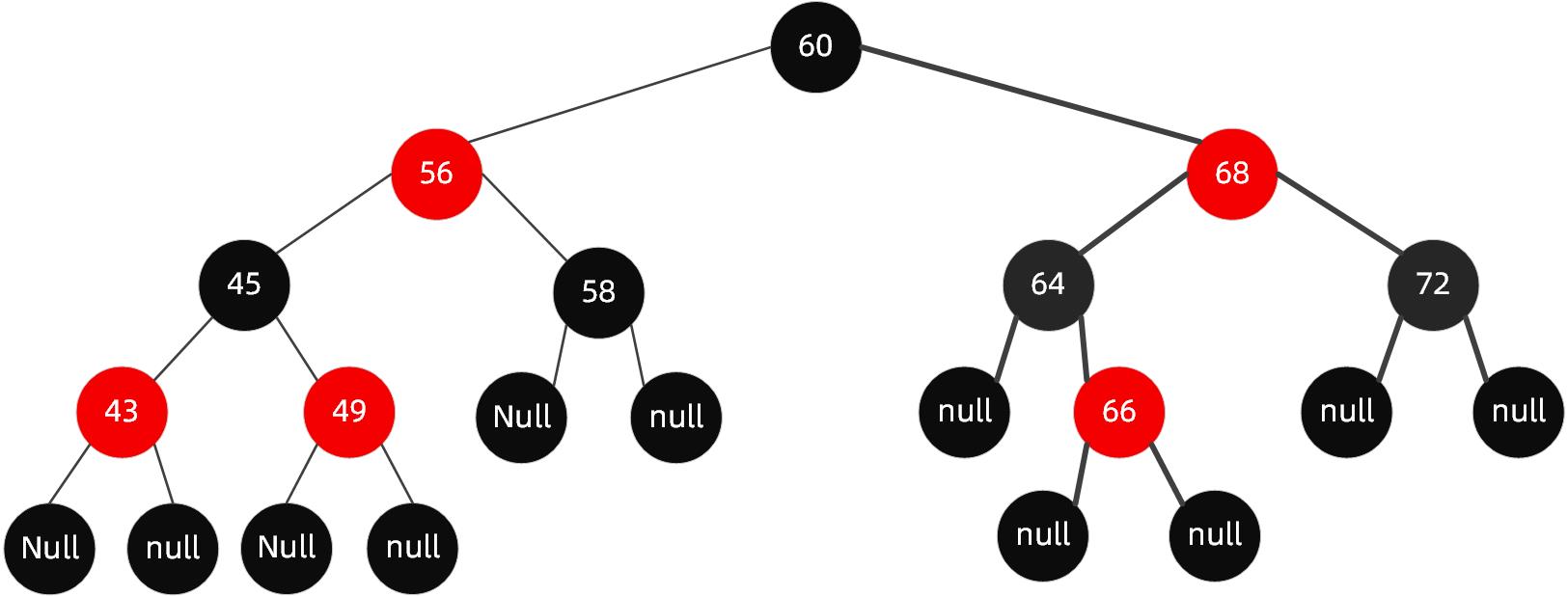
很明显,这个时候结构依然遵循着上述5大特性,无需启动自动平衡机制调整节点平衡状态。
如果再向里面插入值为51的节点呢,这个时候红黑树变成了这样。
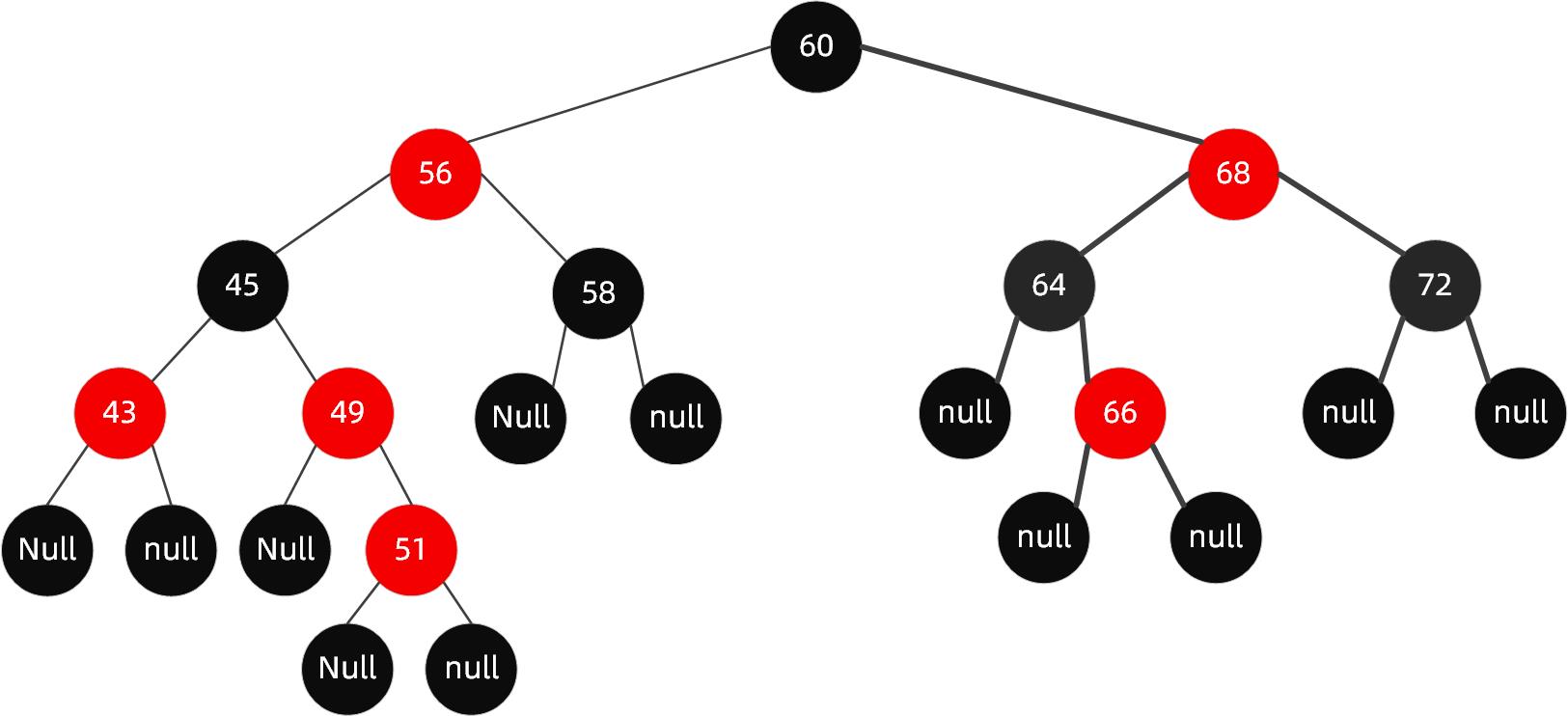
这样的结构实际上是不满足性质4的,红色两个子节点必须是黑色的,而这里49这个红色节点现在有个51的红色节点与其相连。
这个时候我们需要调整这个树的结构来保证红黑树的平衡。
首先尝试将49这个节点设置为黑色,如下示意图。
这个时候我们发现黑高是不对的,其中 60-56-45-49-51-null 这条路径有 4 个黑节点,其他路径的黑色节点是 3 个。
接着调整红黑树,我们再次尝试把45这个节点设置为红色的,如下图所示:
这个时候我们发现问题又来了,56-45-43 都是红色节点的,出现了红色节点相连的问题。
于是我们需要再把 56 和 43 设置为黑色的,如下图所示。
于是我们把 68 这个红色节点设置为黑色的。
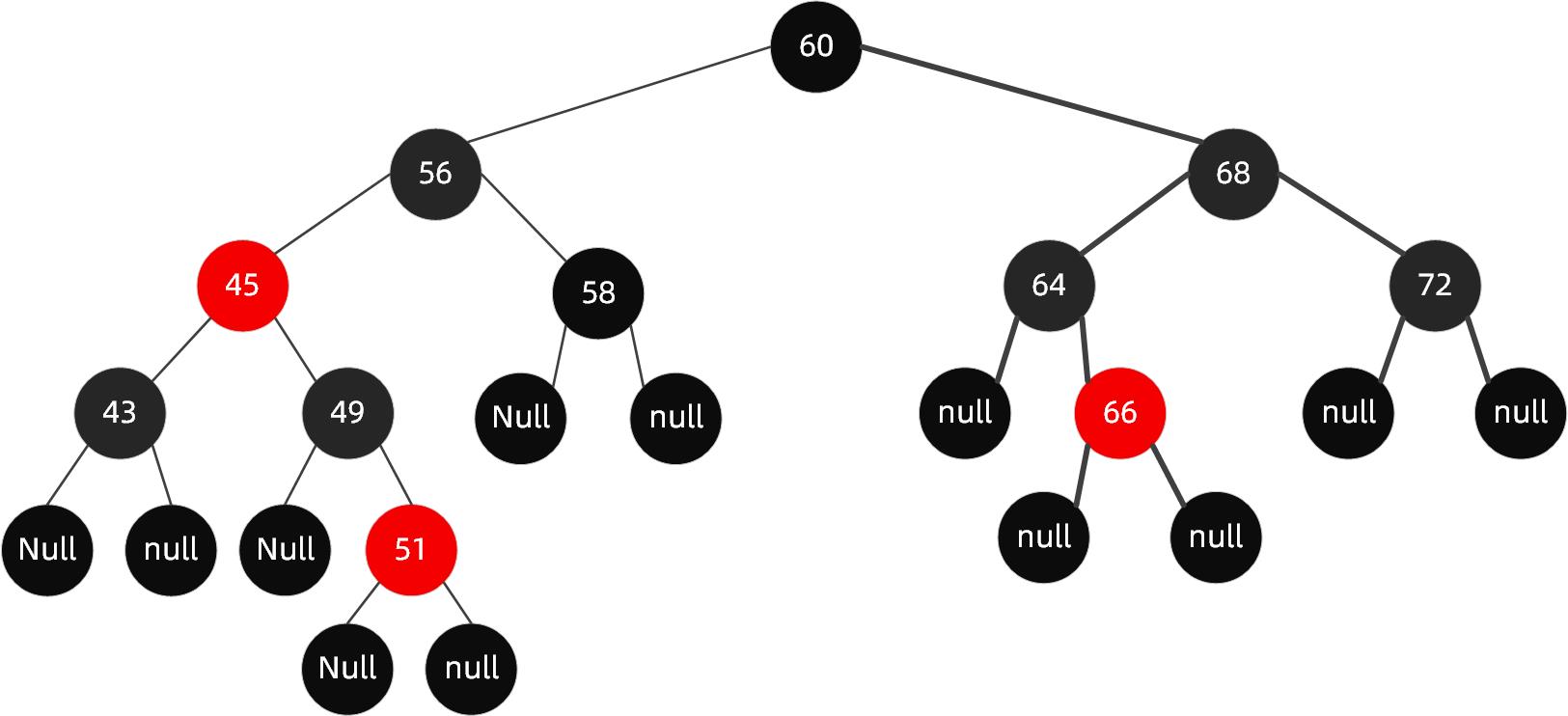
对于这种红黑树插入节点的情况下,我们可以只需要通过变色就可以保持树的平衡了。但是并不是每次都是这么幸运的,当变色行不通的时候,我们需要考虑另一个手段就是旋转了。
例如下面这种情况,同样还是拿这颗红黑树举例。

现在这颗红黑树,我们现在插入节点65。
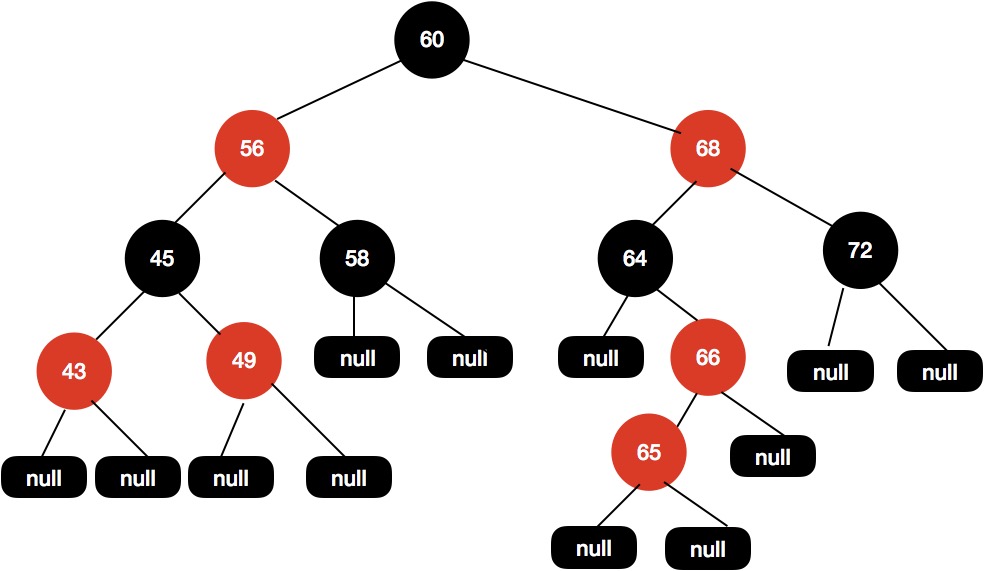
我们尝试把 66 这个节点设置为黑色,如下图所示。
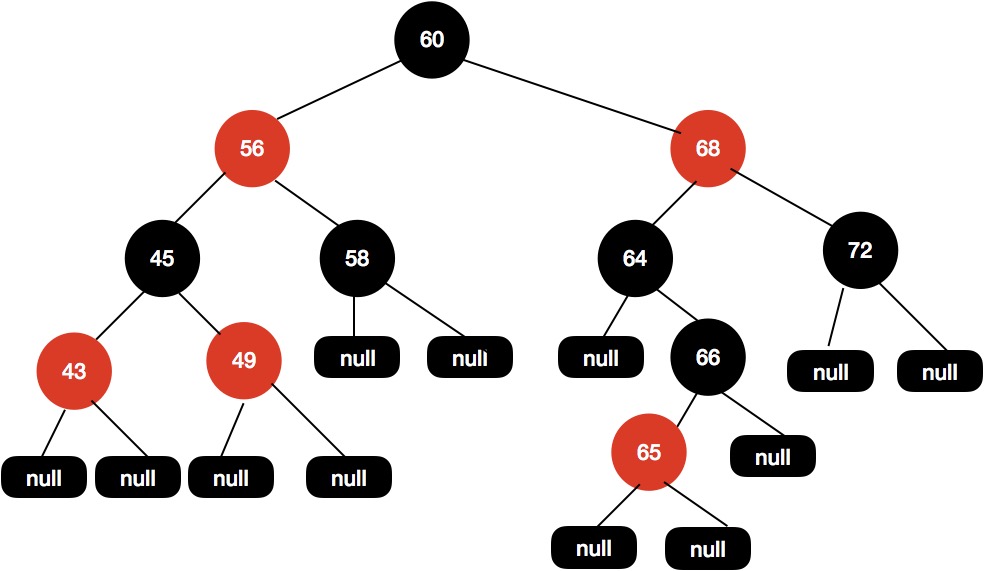
这样操作之后黑高又出现不一致的情况了,60-68-64-null 有 3 个黑色节点,而60-68-64-66-null 这条路径有 4 个黑色节点,这样的结构是不平衡的。
或者我们把 68 设置为黑色,把 64 设置为红色,如下图所示:
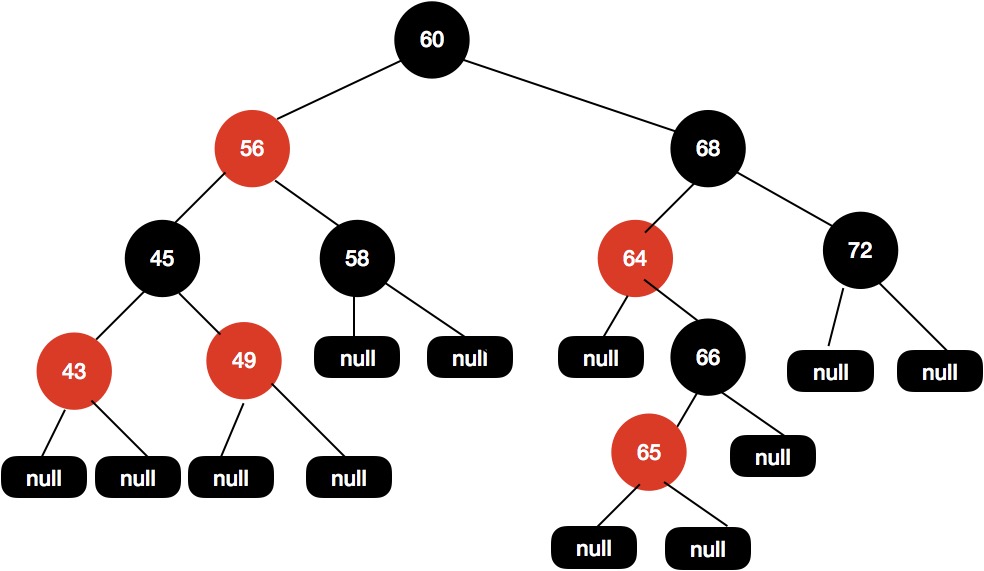
但是,同样的问题,上面这颗红黑树的黑色高度还是不一致,60-68-64-null 和 60-68-64-66-null 这两条路径黑色高度还是不一致。
这种情况如果只通过变色的情况是不能保持红黑树的平衡的。
红黑树的旋转
接下来我们讲讲红黑树的旋转,旋转分为左旋和右旋。
左旋
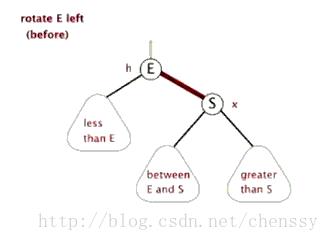
文字描述:逆时针旋转两个节点,让一个节点被其右子节点取代,而该节点成为右子节点的左子节点。
文字描述太抽象,接下来看下图片展示。
首先断开节点PL与右子节点G的关系,同时将其右子节点的引用指向节点C2;然后断开节点G与左子节点C2的关系,同时将G的左子节点的应用指向节点PL。

接下来再放下 gif 图,希望能帮助大家更好地理解左旋,图片来自网络。
右旋
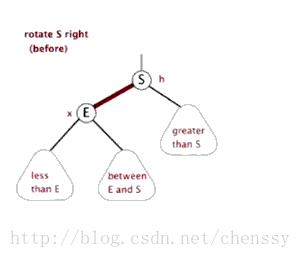
文字描述:顺时针旋转两个节点,让一个节点被其左子节点取代,而该节点成为左子节点的右子节点。
右旋的图片展示:
首先断开节点G与左子节点PL的关系,同时将其左子节点的引用指向节点C2;然后断开节点PL与右子节点C2的关系,同时将PL的右子节点的应用指向节点G。

右旋的gif展示(图片来自网络):
介绍完了左旋和右旋基本操作,我们来详细介绍下红黑树的几种旋转场景。
左左节点旋转(插入节点的父节点是左节点,插入节点也是左节点)
如下图所示的红黑树,我们插入节点是65。
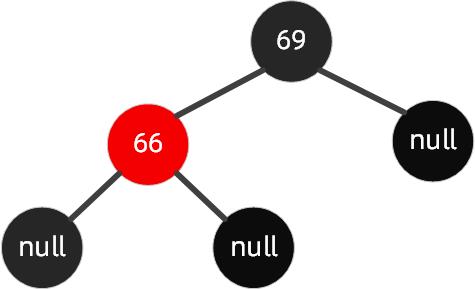
操作步骤如下可以围绕祖父节点 69 右旋,再结合变色,步骤如下所示:
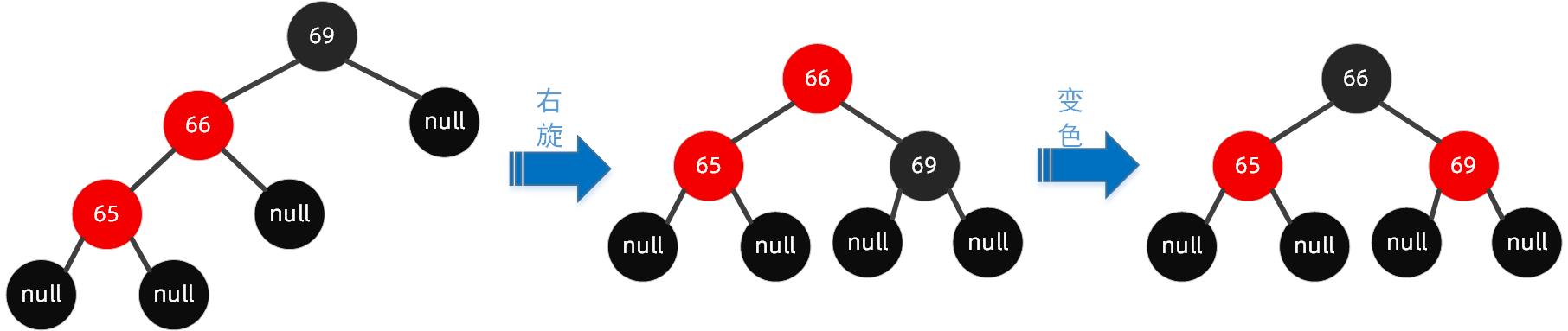
左右节点旋转(插入节点的父节点是左节点,插入节点是右节点)
还是上面这颗红黑树,我们再插入节点 67。

这种情况我们可以这样操作,先围绕父节点 66 左旋,然后再围绕祖父节点 69 右旋,最后再将 67 设置为黑色,把 69 设置为红色,如下图所示。

右左节点旋转(插入节点的父节点是右节点,插入节点左节点)
如下图这种情况,我们要插入节点68。
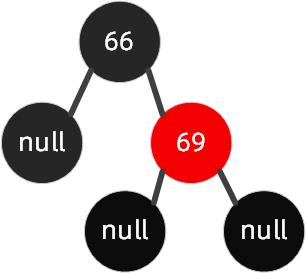
这种情况,我们可以先围绕父节点 69 右旋,接着再围绕祖父节点 66 左旋,最后把 68 节点设置为黑色,把 66 设置为红色,我们的具体操作步骤如下所示。

右右节点旋转(插入节点的父节点是右节点,插入节点也是右节点)
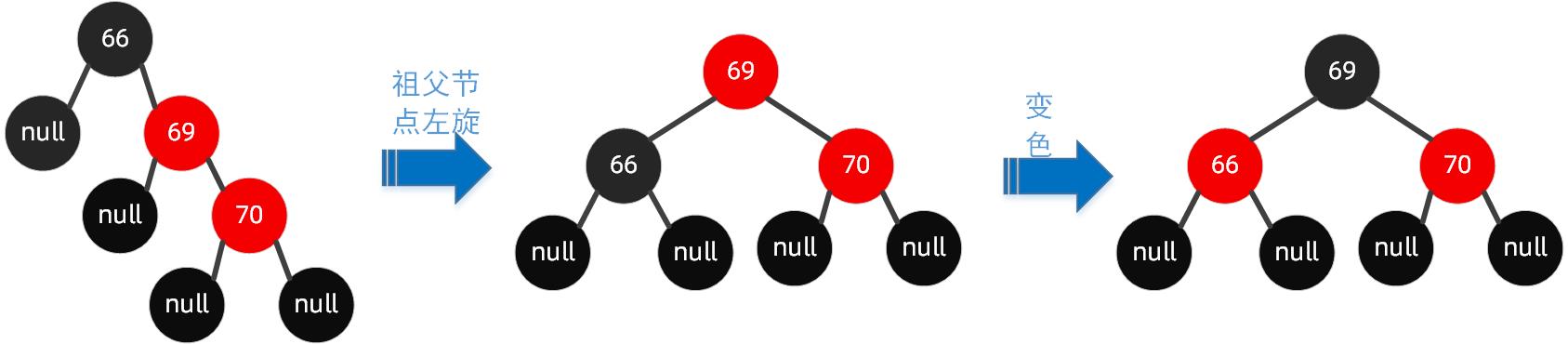
还是来上面的图来举例,我们在这颗红黑树上插入节点 70 。

我们可以这样操作围绕祖父节点 66 左旋,再把旋转后的根节点 69 设置为黑色,把 66 这个节点设置为红色。具体可以参看下图:
红黑树在 Java 中的实现
Java 中的红黑树实现类是 TreeMap ,接下来我们尝试从源码角度来逐行解释 TreeMap 这一套机制是如何运作的。
// TreeMap中使用Entry来描述每个节点
static final class Entry<K,V> implements Map.Entry<K,V>
K key;
V value;
Entry<K,V> left;
Entry<K,V> right;
Entry<K,V> parent;
boolean color = BLACK;
...
TreeMap 的put方法。
public V put(K key, V value)
//先以t保存链表的root节点
Entry<K,V> t = root;
//如果t=null,表明是一个空链表,即该TreeMap里没有任何Entry作为root
if (t == null)
compare(key, key); // type (and possibly null) check
//将新的key-value创建一个Entry,并将该Entry作为root
root = new Entry<>(key, value, null);
size = 1;
//记录修改次数加1
modCount++;
return null;
int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
//如果比较器cpr不为null,即表明采用定制排序
if (cpr != null)
do
//使用parent上次循环后的t所引用的Entry
parent = t;
//将新插入的key和t的key进行比较
cmp = cpr.compare(key, t.key);
//如果新插入的key小于t的key,t等于t的左边节点
if (cmp < 0)
t = t.left;
//如果新插入的key大于t的key,t等于t的右边节点
else if (cmp > 0)
t = t.right;
else
//如果两个key相等,新value覆盖原有的value,并返回原有的value
return t.setValue(value);
while (t != null);
else
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
while (t != null);
//将新插入的节点作为parent节点的子节点
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新插入key小于parent的key,则e作为parent的左子节点
if (cmp < 0)
parent.left = e;
//如果新插入key小于parent的key,则e作为parent的右子节点
else
parent.right = e;
//修复红黑树
fixAfterInsertion(e);
size++;
modCount++;
return null;
//插入节点后修复红黑树
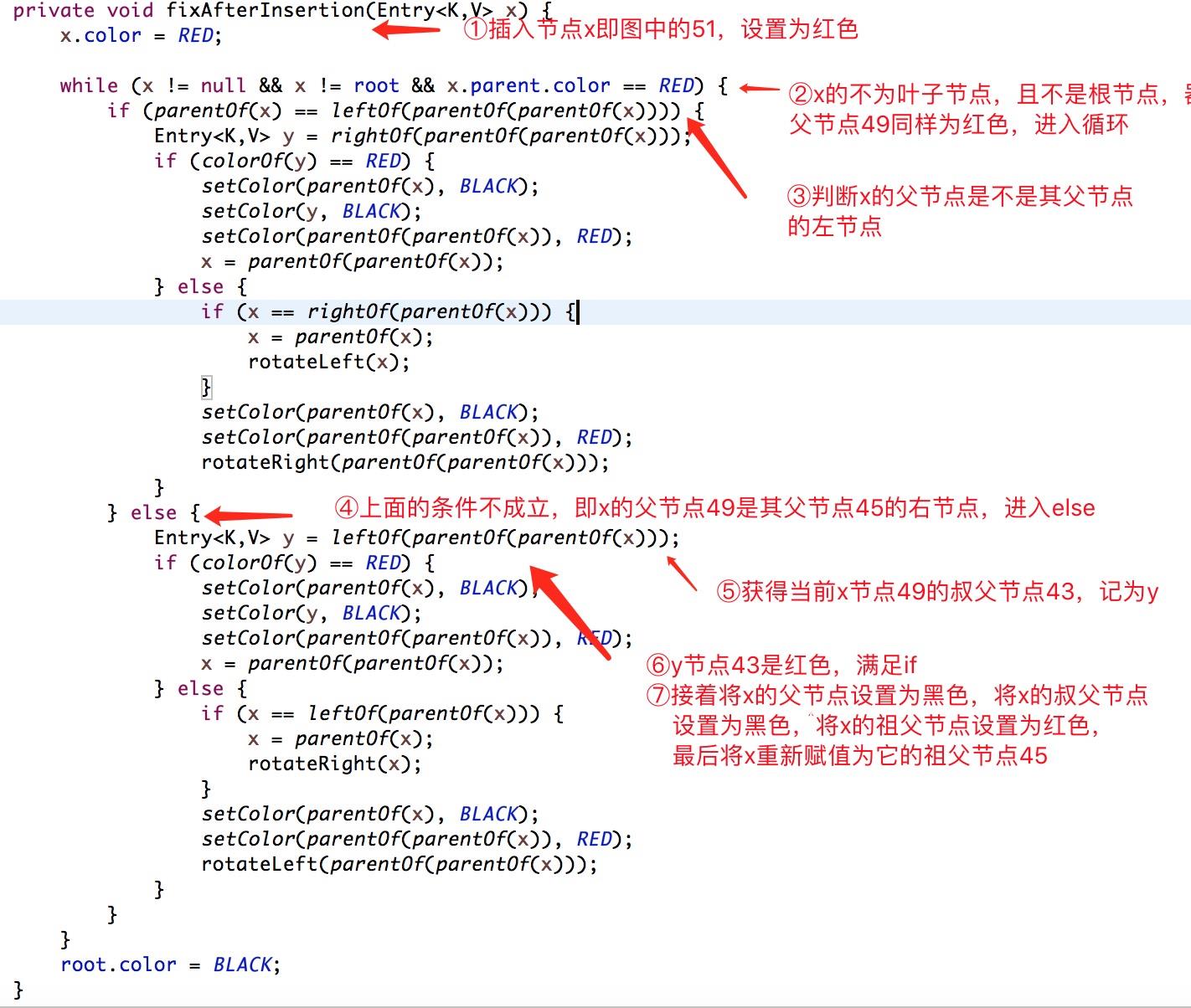
private void fixAfterInsertion(Entry<K,V> x)
x.color = RED;
//直到x节点的父节点不是根,且x的父节点是红色
while (x != null && x != root && x.parent.color == RED)
//如果x的父节点是其父节点的左子节点
if (parentOf(x) == leftOf(parentOf(parentOf(x))))
//获取x的父节点的兄弟节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果x的父节点的兄弟节点是红色
if (colorOf(y) == RED)
//将x的父节点设置为黑色
setColor(parentOf(x), BLACK);
//将x的父节点的兄弟节点设置为黑色
setColor(y, BLACK);
//将x的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
//如果x的父节点的兄弟节点是黑色
else
//TODO 对应情况第二种,左右节点旋转
//如果x是其父节点的右子节点
if (x == rightOf(parentOf(x)))
//将x的父节点设为x
x = parentOf(x);
//右旋转
rotateLeft(x);
//把x的父节点设置为黑色
setColor(parentOf(x), BLACK);
//把x的父节点父节点设为红色
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
//如果x的父节点是其父节点的右子节点
else
//获取x的父节点的兄弟节点
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//只着色的情况对应的是最开始例子,没有旋转操作,但是要对应多次变换
//如果x的父节点的兄弟节点是红色
if (colorOf(y) == RED)
//将x的父节点设置为黑色
setColor(parentOf(x), BLACK);
//将x的父节点的兄弟节点设为黑色
setColor(y, BLACK);
//将X的父节点的父节点(G)设置红色
setColor(parentOf(parentOf(x)), RED);
//将x设为x的父节点的节点
x = parentOf(parentOf(x));
//如果x的父节点的兄弟节点是黑色
else
//如果x是其父节点的左子节点
if (x == leftOf(parentOf(x)))
//将x的父节点设为x
x = parentOf(x);
//右旋转
rotateRight(x);
//将x的父节点设为黑色
setColor(parentOf(x), BLACK);
//把x的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
//将根节点强制设置为黑色
root.color = BLACK;
TreeMap的插入节点和普通的排序二叉树没啥区别,唯一不同的是,在TreeMap 插入节点后会调用方法fixAfterInsertion(e)来重新调整红黑树的结构来让红黑树保持平衡。
我们重点关注下红黑树的fixAfterInsertion(e)方法,接下来我们来分别介绍两种场景来演示fixAfterInsertion(e)方法的执行流程。
第一种场景:只需变色即可平衡
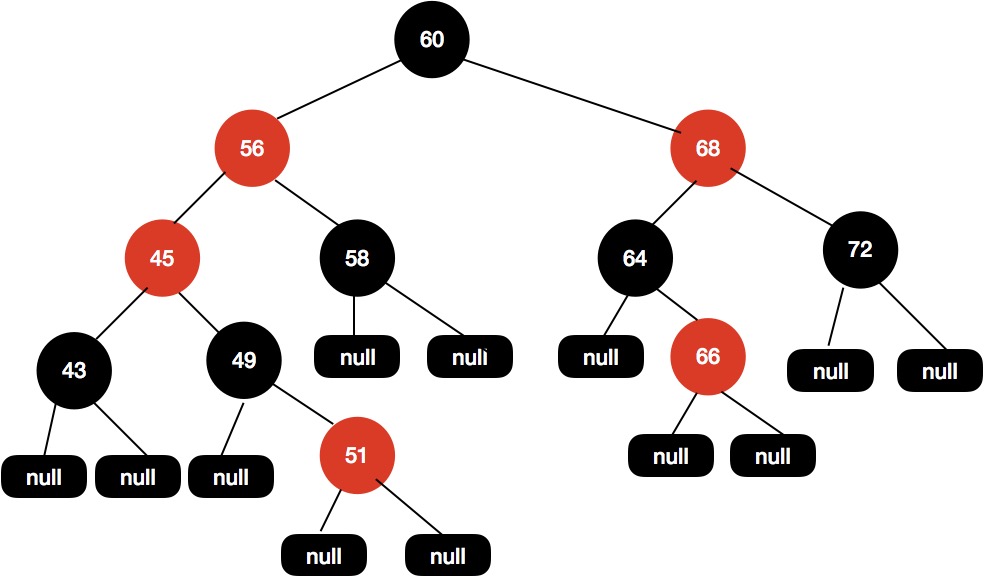
同样是拿这颗红黑树举例,现在我们插入节点 51。

当我们需要插入节点51的时候,这个时候TreeMap 的 put 方法执行后会得到下面这张图。

接着调用fixAfterInsertion(e)方法,如下代码流程所示。
当第一次进入循环后,执行后会得到下面的红黑树结构。
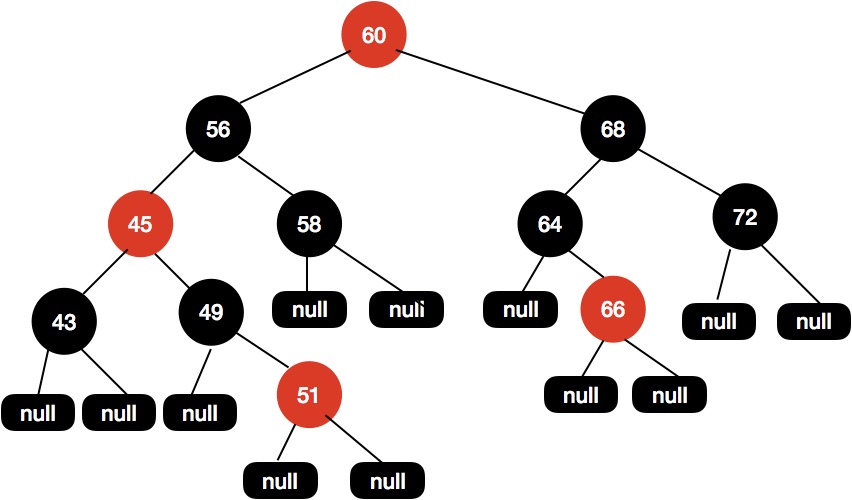
在把 x 重新赋值后,重新进入 while 循环,此时的 x 节点为 45 。

执行上述流程后,得到下面所示的红黑树结构。
这个时候x被重新赋值为60,因为60是根节点,所以会退出 while 循环。在退出循序后,会再次把根节点设置为黑色,得到最终的结构如下图所示。
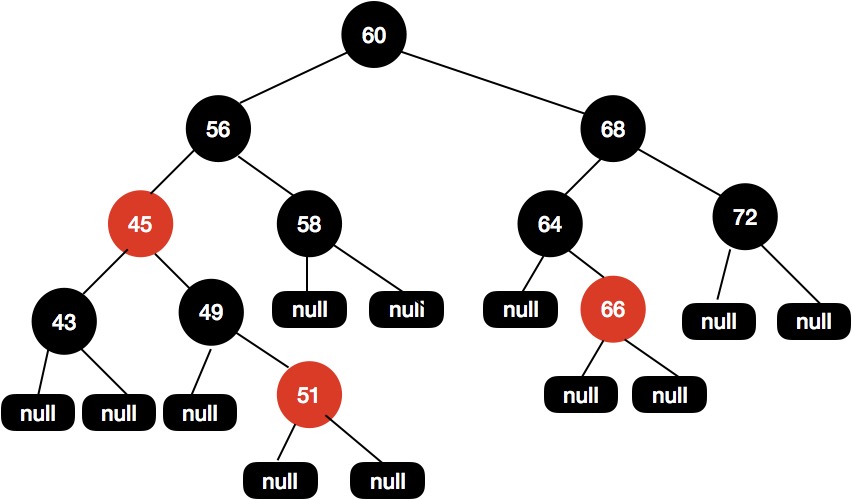
最后经过两次执行while循环后,我们的红黑树会调整成现在这样的结构,这样的红黑树结构是平衡的,所以路径的黑高一致,并且没有红色节点相连的情况。
第二种场景 旋转搭配变色来保持平衡
接下来我们再来演示第二种场景,需要结合变色和旋转一起来保持平衡。
给定下面这样一颗红黑树:
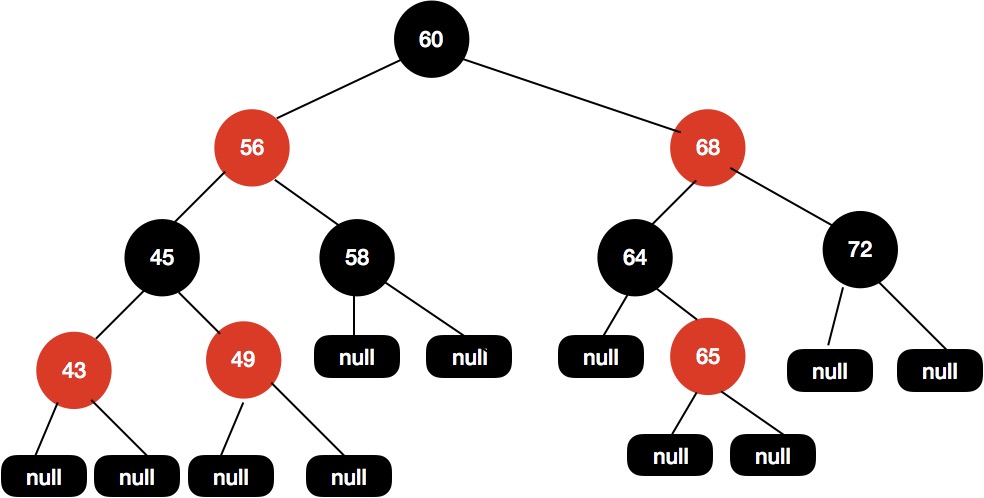
现在我们插入节点66,得到如下树结构。
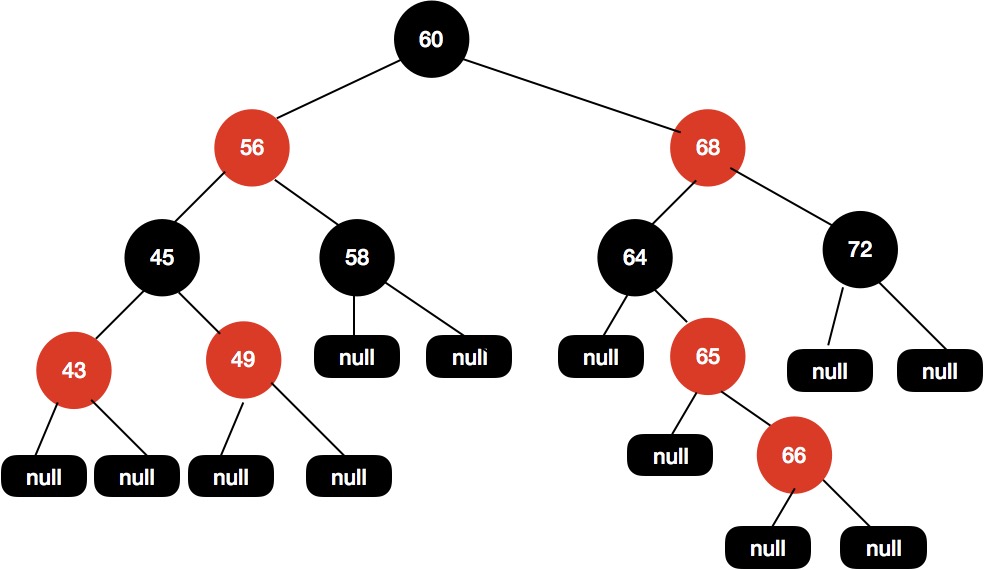
同样地,我们进入fixAfterInsertion(e)方法。

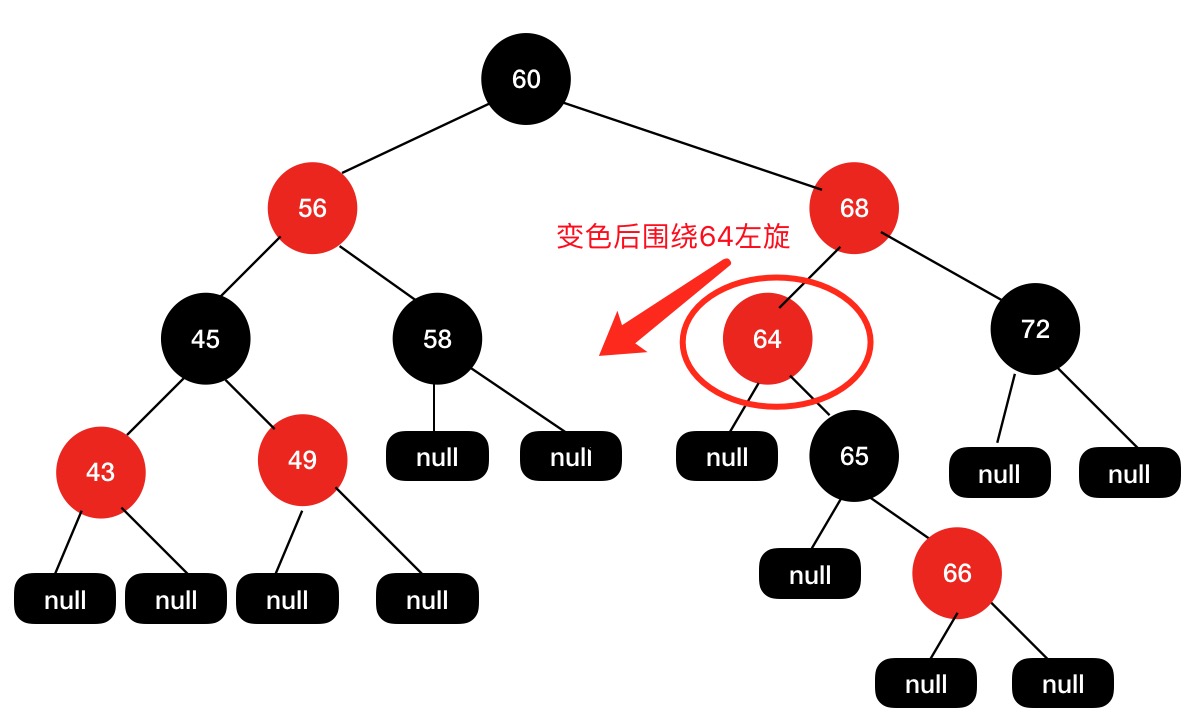
最终我们得到的红黑树结构如下图所示:
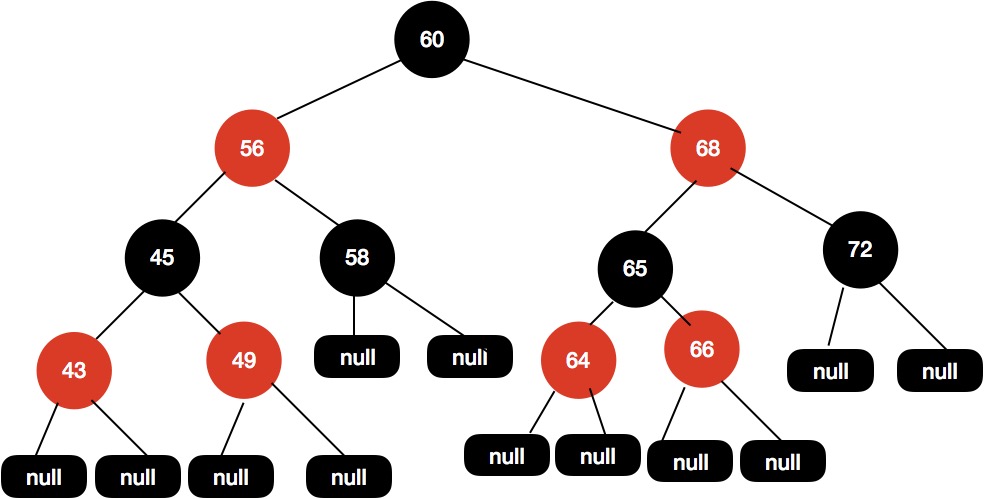
调整成这样的结构我们的红黑树又再次保持平衡了。
演示 TreeMap 的流程就拿这两种场景举例了,其他的就不一一举例了。
红黑树的删除
因为之前的分享只整理了红黑树的插入部分,本来想着红黑树的删除就不整理了,有人跟我反馈说红黑树的删除相对更复杂,于是索性还是把红黑树的删除再整理下。
删除相对插入来说,的确是要复杂一点,但是复杂的地方是因为在删除节点的这个操作情况有很多种,但是插入不一样,插入节点的时候实际上这个节点的位置是确定的,在节点插入成功后只需要调整红黑树的平衡就可以了。
但是删除不一样的是,删除节点的时候我们不能简单地把这个节点设置为null,因为如果这个节点有子节点的情况下,不能简单地把当前删除的节点设置为null,这个被删除的节点的位置需要有新的节点来填补。这样一来,需要分多种情况来处理了。
删除节点是根节点
直接删除根节点即可。
删掉节点的左子节点和右子节点都是为空
直接删除当前节点即可。
删除节点有一个子节点不为空
这个时候需要使用子节点来代替当前需要删除的节点,然后再把子节点删除即可。
给定下面这棵树,当我们需要删除节点69的时候。
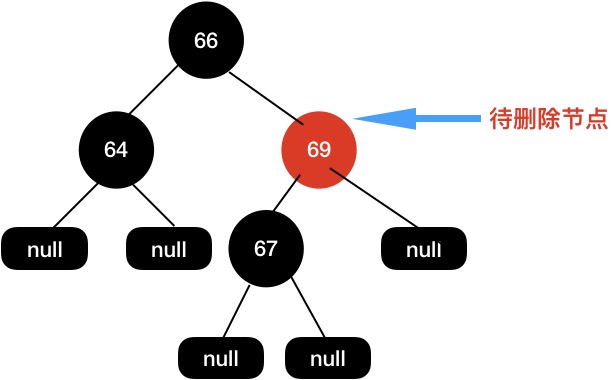
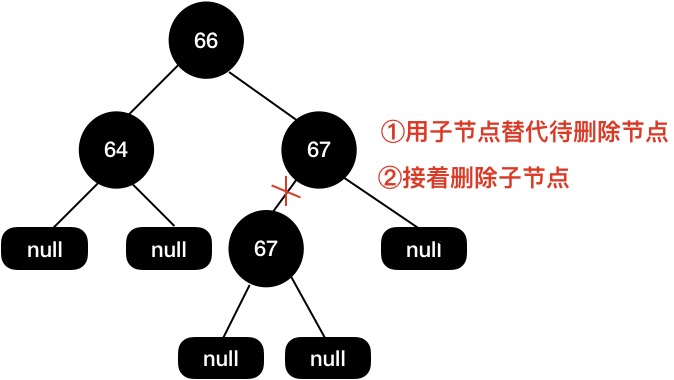
首先用子节点代替当前待删除节点,然后再把子节点删除。
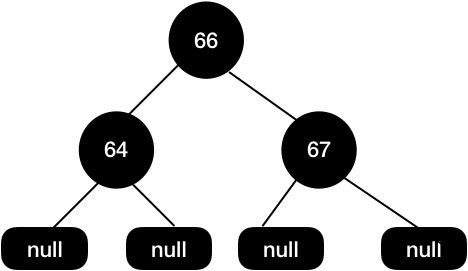
最终的红黑树结构如下面所示,这个结构的红黑树我们是不需要通过变色+旋转来保持红黑树的平衡了,因为将子节点删除后树已经是平衡的了。
还有一种场景是当我们待删除节点是黑色的,黑色的节点被删除后,树的黑高就会出现不一致的情况,这个时候就需要重新调整结构。
还是拿上面这颗删除节点后的红黑树举例,我们现在需要删除节点67。
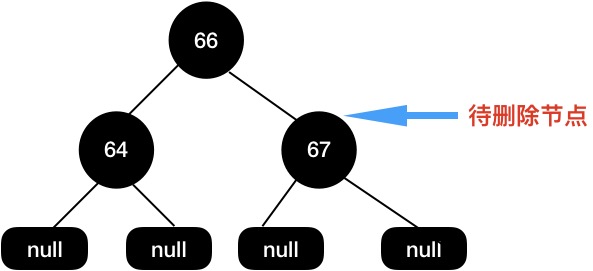
因为67 这个节点的两个子节点都是null,所以直接删除,得到如下图所示结构:
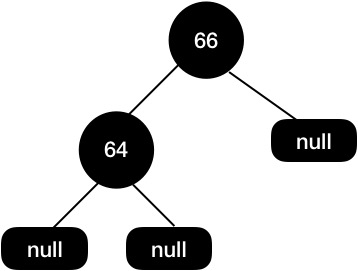
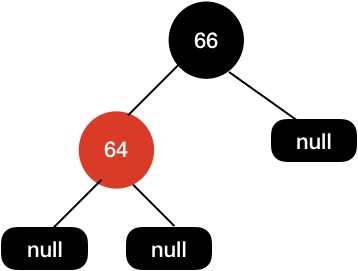
这个时候我们树的黑高是不一致的,左边黑高是3,右边是2,所以我们需要把64节点设置为红色来保持平衡。
删除节点两个子节点都不为空
删除节点两个子节点都不为空的情况下,跟上面有一个节点不为空的情况下也是有点类似,同样是需要找能替代当前节点的节点,找到后,把能替代删除节点值复制过来,然后再把替代节点删除掉。
- 先找到替代节点,也就是前驱节点或者后继节点
- 然后把前驱节点或者后继节点复制到当前待删除节点的位置,然后在删除前驱节点或者后继节点。
那么什么叫做前驱,什么叫做后继呢?
前驱是左子树中最大的节点,后继则是右子树中最小的节点。
前驱或者后继都是最接近当前节点的节点,当我们需要删除当前节点的时候,也就是找到能替代当前节点的节点,能够替代当前节点肯定是最接近当前节点。
在当前删除节点两个子节点不为空的场景下,我们需要再进行细分,主要分为以下三种情况。
第一种,前驱节点为黑色节点,同时有一个非空节点
如下面这样一棵树,我们需要删除节点64:
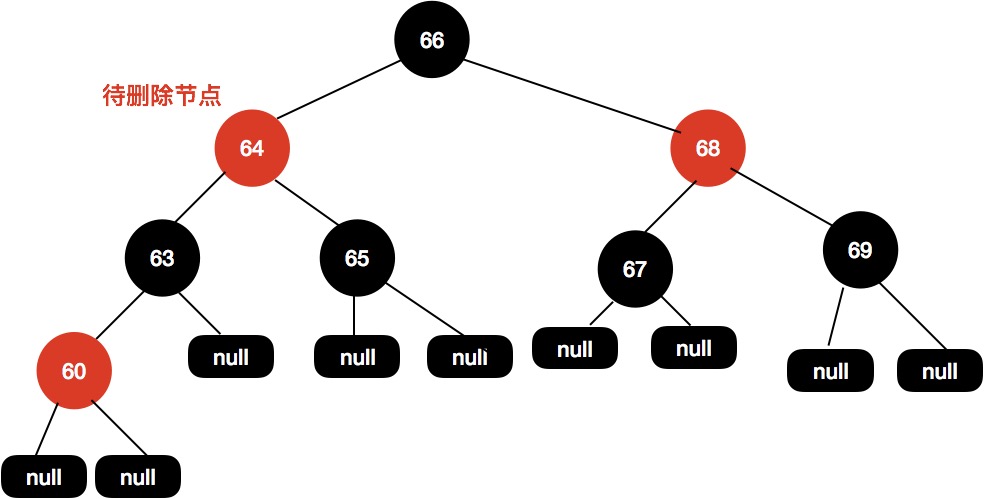
首先找到前驱节点,把前驱节点复制到当前节点:
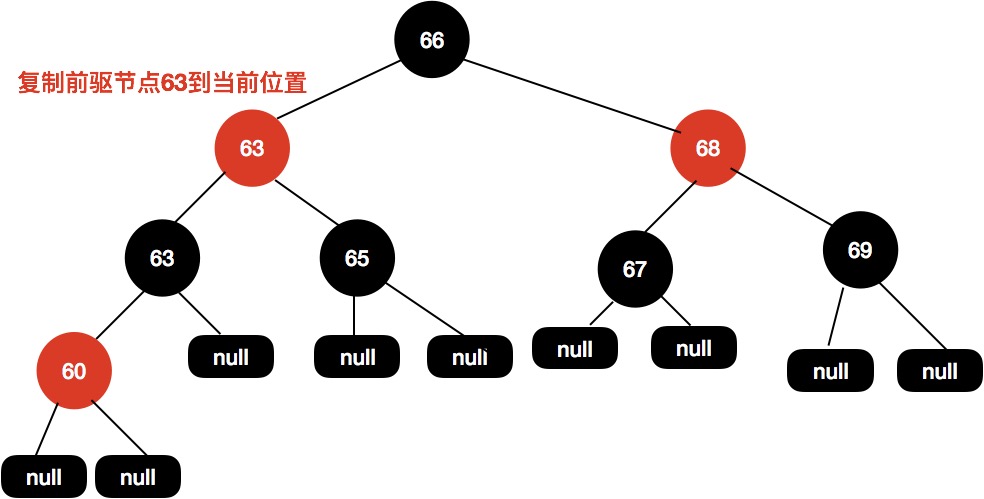
接着删除前驱节点。
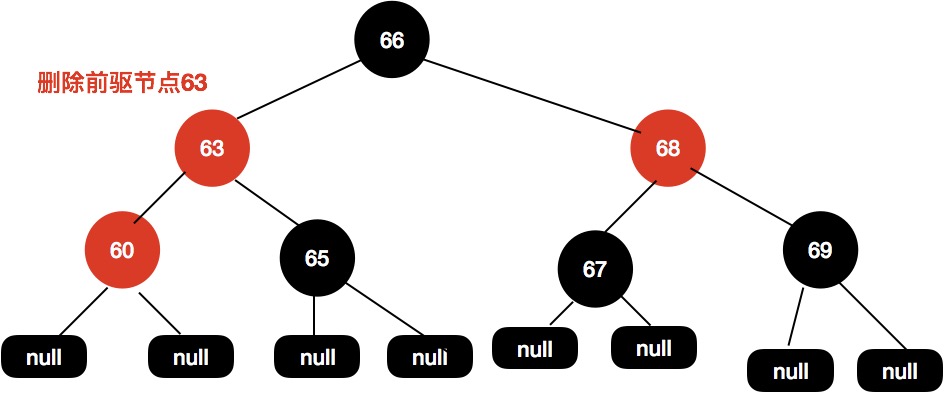
这个时候63和60这个节点都是红色的,我们尝试把60这个节点设置为红色即可使整个红黑树达到平衡。
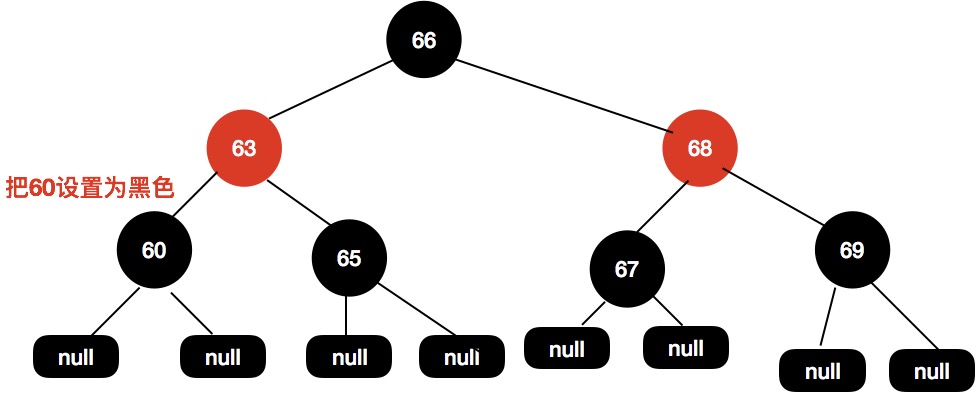
第二种,前驱节点为黑色节点,同时子节点都为空
前驱节点是黑色的,子节点都为空,这个时候操作步骤与上面基本类似。
如下操作步骤:
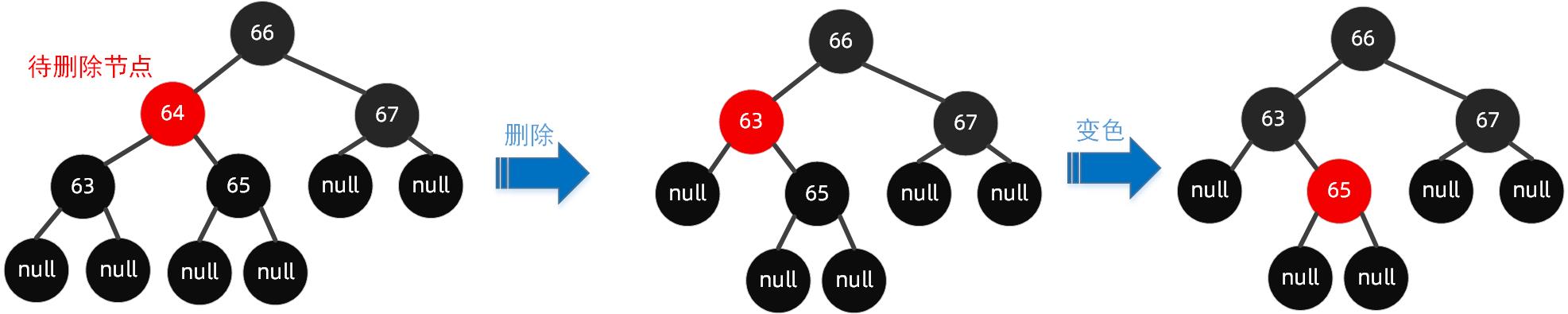
因为要删除节点64,接着找到前驱节点63,把63节点复制到当前位置,然后将前驱节点63删除掉,变色后出现黑高不一致的情况下,最后把63节点设置为黑色,把65节点设置为红色,这样就能保证红黑树的平衡。
第三种,前驱节点为红色节点,同时子节点都为空
给定下面这颗红黑树,我们需要删除节点64的时候。
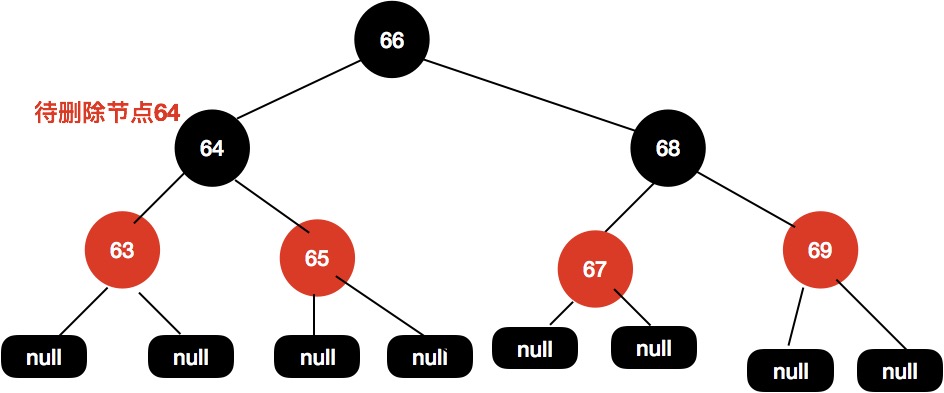
同样地,我们找到64的前驱节点63,接着把63赋值到64这个位置。
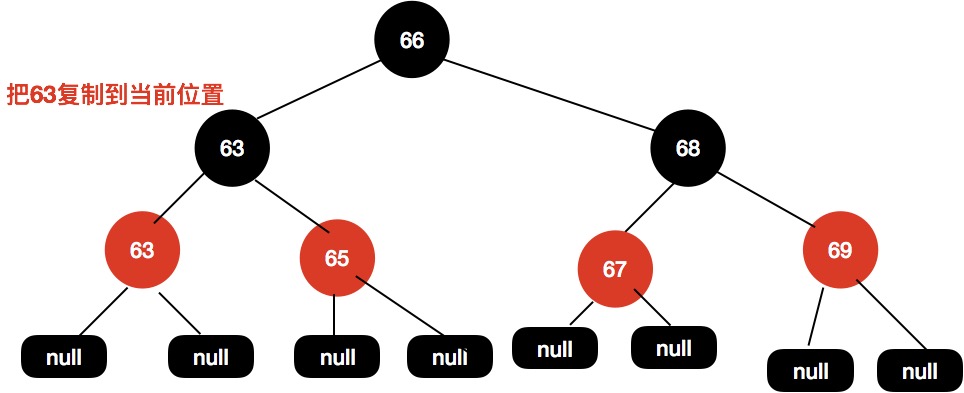
然后删除前驱节点。
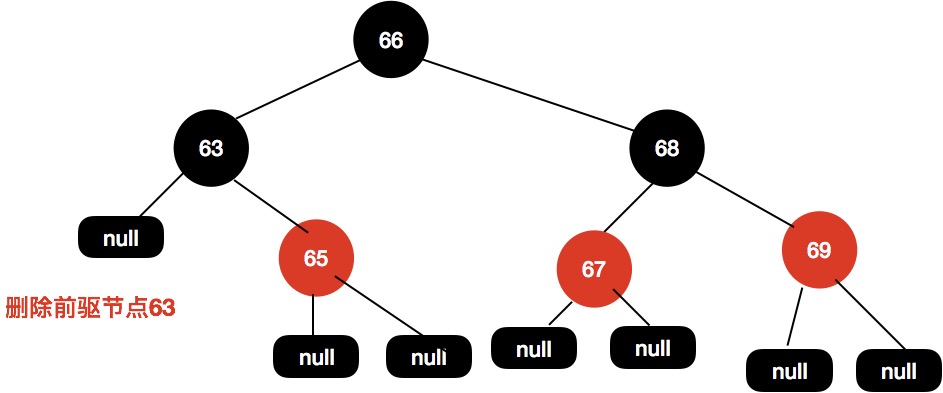
删除节点后不需要变色也不需要旋转即可保持树的平衡。
终于把红黑树的基本原理部分写完了,用了很多示意图,这篇文章是在之前分享的 ppt 上再整理出来,我觉得自己应该算是把基本操作讲明白了,整理这篇文章前前后后用了近一周左右,因为平时上班,基本上只有周末有时间才有时间整理,如有问题请留言讨论。
如果您觉得写得还可以,请您帮忙点个赞,您的点赞真的是对我最大的支持,也是我能继续写下去的动力,感谢。
文章中很多参考了下面文章的一些示意图,非常感谢以下文章。
What does the time complexity O(log n) actually mean?
以上是关于我画了25张图展示线程池工作原理和实现原理,原创干货,建议先收藏再阅读的主要内容,如果未能解决你的问题,请参考以下文章