机器学习3：SVM——软间隔&核函数（中）

Posted 2021-04-03 我走过的地方越来越多

来都来了，不关注下吗？？

   

大家好，明天就是正月十五啦，提前祝大家元宵节快乐哦！ 应付七大姑八大姨的任务结束，终于要走上正轨喵~~

本来觉得SVM分两次可以写完，结果今天发现内容有点多，所以还是决定分上 中 下 三次介绍。（写太长看的也太费劲了）

那么我们废话不多说。上一篇相信大家已经知道了该怎么去找最优的超平面，但如果样本有噪音该怎么办呢？比如：

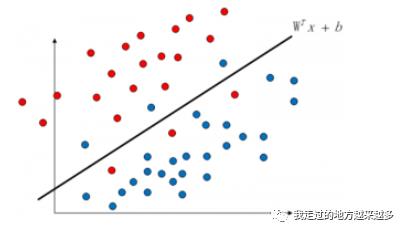
按照之前的算法，这个超平面就没法计算出来了，因为我们不可能找到一条这样的直线去满足之前的约束。所以在这里要引入一个新的概念——软间隔

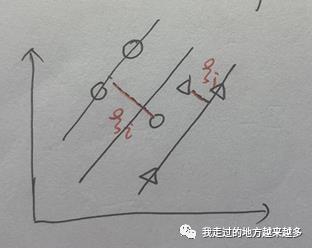
我们都知道原式yi(wx+b)≥1保证的是所有的样本点与超平面的距离都大于1，那么现在引入一个松弛变量，比如说松弛变量为0.1，那么所有样本之间的距离只需要大于0.9即可，如果噪音仍然不能被包含进去，那就再增大一点松弛变量。就像它的名字一样，将距离的要求进行放宽，以此满足噪音的情况。

    于此同时我们的约束也要修改：

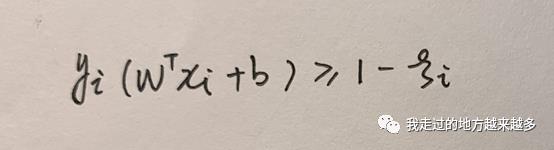
所以最终：

在min式子中新加入了松弛变量的求和项，称为惩罚项。就像名字说的一样，我们不能一味地去放宽限制以此来满足噪音的存在，如果放宽的太多了，min式子就会相应的变大，也就不再是求最小问题了，这时候需要惩罚。C是调和系数，如果C很小，那么松弛变量就能相应地设置得大一点，因为乘上C之后在总式子中体现地就很小了。C决定了我们想让这个SVM有多软还是多硬。

软间隔还是比较简单的，总体来说引入了松弛变量和C之后，最大的变化是根据KKT条件得到0≤lambda_i ≤C，之后所有发生的变化都是围绕着lambda的范围改变而展开的。最后得到：

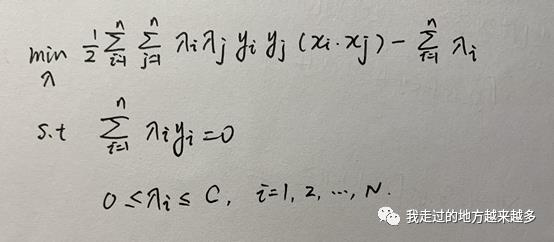
之后我们要做的就是求得满足条件的所有lambda_i的值，然后再以此求得

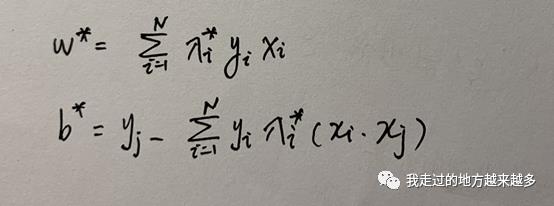
非线性SVM

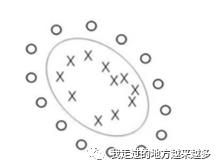
上一篇也提到了，在上图这种情况下，用一个线性的超平面就不太够了。所以我们的超平面是上图中的一个圆圈？这好像不太对劲。但是我们都知道样本中的每一个点都是真实的点，我们也许就在二维平面上表示是不太够的，也许我们在三维空间中将样本一个个地描述出来是下面这样的。

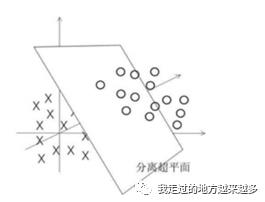
那在三维中我们依然可以用一个超平面去表示。但是大家不禁会有疑惑：

你怎么就能确信在三维中一定是上面这张图？如果他们依然是一类点在中间，另一类点把它包住呢？

这是完全可能存在的！所以我们需要到拓展到四维的情况下再去判断。

这就好像一场博弈，我们每失败一次，就升维一次，直到某一维N时两类点出现了一个失误，他们线性可分了。这就是SVM解决线性不可分的过程，但它并不是逐渐升维的，而是直接上升到无穷维。

为什么是无穷维？

我们去找具体是第几维的这种过程太复杂了，事实上我们的维度只需要大于等于N维就可以了，所以考虑到所有的应用场景、不同问题下的样本特征，我们直接上升到无穷维使得其必定可以线性可分。

 

为什么样本随着维度的升高一定是线性可分的？有没有存在无穷维也不可分的情况呢？

没有，样本之间只要存在差异，也就是说只要不是相同的样本点，一定能在某种程度上对其进行区分。就好像上面的例子一样，我们无法划分，只是维度太低观察到的信息不够。随着维度的上升，我们的信息量越来越充足，只要是有差异的样本并且找到其差异，一定能够使用该差异来划分的。

 

为什么大于N维也可以？会不会存在大于N维的某一维又突然线性不可分了呢？

不会，就像上一个问题一样，当你在某一维突然获取到了能够划分样本的足够多的信息后，随着维度的上升，我们得到的信息量只会越来越多，而第N维的信息量就足够我们划分了，更多的信息量并不会出现问题中的这种情况。

 数学的直观角度上来讲，SVM中升维的过程本质上是变换坐标轴，就好像捏橡皮泥一样不停地变换内部的图形，而升的维度越高，变形也就能越复杂，到最后也就越能直接线性可分。

下面还是先回到我们的loss上面：

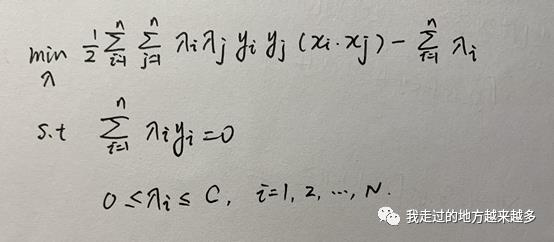
我们看min后面这个式子，其中lambda和y都是标量，直接计算就可以，唯一让人头疼的是xi与xj的点乘，它是向量之间的点乘，同时前面有求和项，也就是说在计算过程中是需要计算任意两个向量之间的点乘的。这就引申出一个问题，如果将全部样本的点乘计算好，计算量太大。例如在Mnist数据集中，每个向量有784维，也就是说单独的两个向量点乘就需要784次运算，再加上6万个样本，其实速度是非常慢的。核函数就是为了解决这个问题而提出的。

关于核函数的有效性及相关证明书上有详细说明，在这里我提一下核函数的核心概念，我们先看一个式子，它就是核函数：

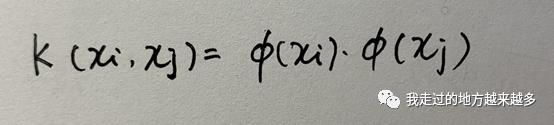
有两个高维向量分别是xi和xj，那么xi和xj的点乘等于上面的K(xi, xj)。什么意思？

我们先将概念理一遍，由于公式的需要，我们目前需要计算向量xi和xj的点乘，我们可以使用核函数将其映射到高维空间去，在高维空间中再运行SVM，使得划分非线性样本成为可能。另一方面，点积的两个样本维度都很高，我们可以使用核函数方便地通过另一种方式去计算，结果是一样的，同样减少了复杂度，使得算法能够在有限的时间内计算完成。

那怎么使用呢？很简单，将上文中所有xi和xj的点乘替换为K(xi, xj)即可。常见的核函数有三种：

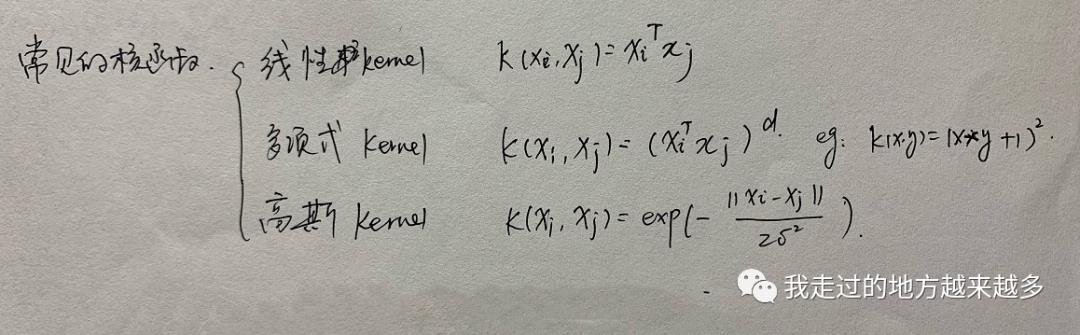
在SVM中我们通常使用的是高斯核，也就是在计算xi和xj的点乘时，只需要计算上面的式子就好了。

到目前为止，SVM的核心思想应该已经全部清楚了。但是你以为结束了吗？不！

下一节我们将介绍SVM最后一个部分——序列最小优化算法（SMO），如何通过多次迭代至收敛求出lambda*。

往期相关：

还不关注喵~~