机器学习15种常用数学符号！

Posted 2022-01-26 Datawhale

↑↑↑关注后"星标"Datawhale

每日干货 & 每月组队学习，不错过

 Datawhale干货 

作者：小雨姑娘，康涅狄格大学，Datawhale成员

这三天复现一个论文实验结果不正确，一直找不到原因，后来发现是自己把当成了如果你到现在搞不懂这两个符号的区别，这问题就跟学英语记不住周一到周日的正确拼写一样严重，那么就非常有必要花3分钟跟着这篇文章复习一遍。

这篇文章的主要内容来自_Mathematical Notation: A Guide for Engineers and Scientists by Edward R. Scheinerman_ ，基本包括了机器学习中大部分常见数学符号。

---

‍‍‍‍‍‍‍1. 变量名约定 

s- 斜体小写字母用做标量 （例如一个数字）

x- 粗体小写字母用做向量 （例如一个2D点）

A- 粗体大写字母用做矩阵 （例如一个3D变换）

θ- 斜体小写希腊字母用做常量和特殊变量 （例如惩罚项的权重）

2. 等号

=表示相等 （值相同）

≠表示不相等 （值不同）

≈表示约等于 （π ≈ 3.14159）

:=表示定义 （A 被定义为 B）

3. 平方根与复数

一个平方根运算是这种形式:

也可以有多次平方运算

复数是形式的表达式， 其中是实数部分，是虚数部分。虚数的定义为。

4. 点与叉

点·和叉×符号根据上下文的不同有不同的用法，下面我们分开讨论：

1. 标量乘法:

两个符号都可以表示简单的标量之间的乘法。下边的写法意思相同

对于非常数的标量我们可以省略符号

2. 向量乘法:

表示向量和标量之间相乘，或两向量的逐元素相乘，我们不用点·或叉×符号，一般使用空心点来表示

有时作者可能会显式定义一个不同的符号，例如圆中点⊙或实心圈●

3. 点乘：

点符号·可用来表示两向量之间的点乘。由于其值是一个标量，通常被叫做标量积（scalar product）。

4. 叉乘：

叉乘符号×可以用来表示两向量的叉乘，由于其值是一个向量，又叫做向量积。

5. 西格玛（sigma）

大写希腊字母Σ(Sigma) 用来表示总和， 换句话说就是对一些数字求和。

这里,i=1是说从1西格玛上边的数字100为止。这些分别为上下边界。"E" 右边的_i_告诉我们求和的是什么。注意这里的范围上下都是闭区间。

6. 大写Pi

大写 Pi 或“大Pi”与sigma非常接近， 不同的是我们用乘法取得一系列数字的乘积。

7. 管道（pipes）

管道符号，就是竖线，根据上下文不同，可以表示不同意思。下边的是3种常见用途，绝对值、模长和行列式。

这3种特性都是描述对象的长度（length）。

1. 绝对值

对于数字x,|x|表示x的绝对值。

2. 欧几里得模长（Euclidean norm）

对于向量v，‖v‖是v的欧几里得模长，在机器学习中被称作2范数(2-norm)，计算方法是向量每个元素的平方根的和再开方。

通常用双竖线表示来避免与_绝对值_ 符号混淆，但有些时候也会看见单竖线。

一般的如果右下角加一个数字，表示k阶范数，什么都不加默认2范数

如果右上角加一个数字就代表范数的k次方。

3. 行列式

对于一个矩阵，对于一个矩阵A，|A|表示矩阵A的行列式，也可以表示它的1范数，这两个值不相同，需要根据上下文考虑。

8. 帽子

在几何里，字母上的 “帽子” 符号用来表示一个单位向量。例如，这是向量a的单位向量。

9. 属于

集合理论中，“属于”符号∈和∋可以被用来描述某物是否为集合中的一个元素。例如：

这里我们有一个数字集A 3, 9, 14 而且我们说3是“属于”这个集合的，一般我们使用花括号表示集合。

10. 常见数字集合

ℝ全体实数集合描述_实数（real numbers）_的集合。他们包括整数，有理数，无理数。

ℚ有理数集合（rational numbers）是可以被表示为分数，或比率（类似⅗）的实数。有理数不能以0作分母。这意味着所有的整数都是有理数，因为可以看成分母为1。换句话说无理数就是不能表示为比率的数，例如 π (PI)。

ℤ整数（integers）是没有小数部分的实数。可为正也可以为负。

ℕ自然数（natural numbers）自然数是正整数或非负整数。取决于所学领域和上下文，集合中可能包含也可能不包含0，所以可以是下边任意一种集合。

ℂ复数是实数与虚数的组合，被视为2D平面上的一个坐标。

11. 撇号（prime）

撇号 (′) 通常用在变量名上，用来描述某物很类似，而不用另起个名来描述它。也可以描述经过一些变换后的“下一个值”。

对于一个函数，撇号通常描述为函数的导函数（derivative）。

使用多个撇号可以用来表示 二阶导函数（derivative）_ƒ′′_或 三阶导函数（derivative）ƒ′′′，之后更高的数字，一般作者会用罗马数字或上标数字表示。

12. 向下取整和向上取整（floor & ceiling）

⌊x⌋和⌈x⌉这种特殊的括号分别用来表示floor和ceil函数。

记住下取整是地板(floor) 那两个小横线在下面，得到的是小的值。

向上取整是天花板(ceiling)那两个小横线在上面，得到的是大的值。

13. 箭头

⇒和→优势被用作表示蕴涵（material implication）逻辑。意思是如果A是true，那么B也是true。箭头可以是左右任何方向⇐⇒，也可以双向⇔。当_A ⇒ B_并且_B ⇒ A_，就是他们是相等的A⇔B。

≪和≫通常用来表示明显（significant）不相等。k≫j也可以表示k的数量级大于j。

与（conjunction）∧和 或（disjunction）∨分别表示逻辑与或操作，类似于程序员的AND和OR操作。

14. 逻辑非（logical negation）

有时候，¬,~和!符号都用来表示逻辑NOT。例如，只有在A为false的时候，¬A为true。

15.  区间

有时函数会处理被一些值限定范围的实数，这样的约束可以用区间（interval）来表示。

例如我们可以表示0和1之间的数，让他们包含或不包含0和1：

不包含0或1 ----- (0, 1)

包含0但不包含1 ----- [0, 1)

不包含0但包含1 ----- (0, 1]

包含0和1 ----- [0, 1]

“整理不易，点赞三连↓

机器学习中的数学：向量求和符号累乘符号

目录

• 一、向量
• • 1.1 什么是向量?
  • 1.2 向量的简单定义及使用
  • 1.3 向量的加法和减法
  • 1.4 标量积
  • 1.5 内积
  • 1.6 向量的模
• 二、求和符号
• 三、累乘符号

一、向量

1.1 什么是向量?

向量 是由几个数横向或纵向排列而成的。数纵向排列的向量叫作 列向量 ，如下式所示的变量就是列向量：
$$\mathbf{x}=\left[\begin{array}{c}6\\ 8\end{array}\right]$$
数横向排列的向量叫作 行向量，如下式所示的变量就是行向量：
$$\mathbf{y}=\left[\begin{array}{cccccc}1& 2& 3& 4& 5& 6\end{array}\right]$$
构成向量的一个一个数叫作元素。向量中的元素个数叫作向量的维度。如上例所示， 为二维列向量， 为四维行向量。如 $$\mathbf{x}$$ 和 $$\mathbf{y}$$ 所示，本文向量使用 字母小写粗体 表示。与向量不同的普通的单个数叫作标量。本文中的标量用 小写斜体 表示，如 x、y。向量右上角的 T 是转置符号，表示将列向量转换为行向量，或者将行向量转换为列向量，如下式所示：
$${\mathbf{y}}^{\mathbf{T}}={\left[\begin{array}{cccccc}1& 2& 3& 4& 5& 6\end{array}\right]}^T=\left[\begin{array}{c}1\\ 2\\ 3\\ 4\\ 5\\ 6\end{array}\right]$$
$${\mathbf{x}}^{\mathbf{T}}={\left[\begin{array}{c}6\\ 8\end{array}\right]}^T=\left[\begin{array}{cc}6& 8\end{array}\right]$$

1.2 向量的简单定义及使用

import numpy as np  # 导入numpy包
x = np.array([6, 8])
print(x)
# 一维的 ndarray 类型没有纵横之分，往往表示为行向量。
# 表示 2 × 2 的二维数组（矩阵）
y = np.array([[1, 2], [3, 4]])  # 列向量
print(y)
z = np.array([[1], [2]])  # 列向量
print(z)
# 向量通常定义为一维 ndarray 类型，必要时可以用二维 ndarray 类型 

# 转置用 变量名.T
print(z.T)
print(z.T.T) # 转置操作对于二维 ndarray 类型有效，但对于一维 ndarray 类型是无效的。

1.3 向量的加法和减法

有如下两个向量：
$$\begin{array}{r}\mathbf{a}=\left[\begin{array}{c}2\\ 1\end{array}\right],\mathbf{b}=\left[\begin{array}{c}1\\ 3\end{array}\right]\end{array}$$
首先进行加法运算。向量的加法运算 是将各个元素相加：
$$\begin{array}{r}\mathbf{a}+\mathbf{b}=\left[\begin{array}{c}2\\ 1\end{array}\right]+\left[\begin{array}{c}1\\ 3\end{array}\right]\end{array}=\left[\begin{array}{c}2+1\\ 1+3\end{array}\right]=\left[\begin{array}{c}3\\ 4\end{array}\right]$$
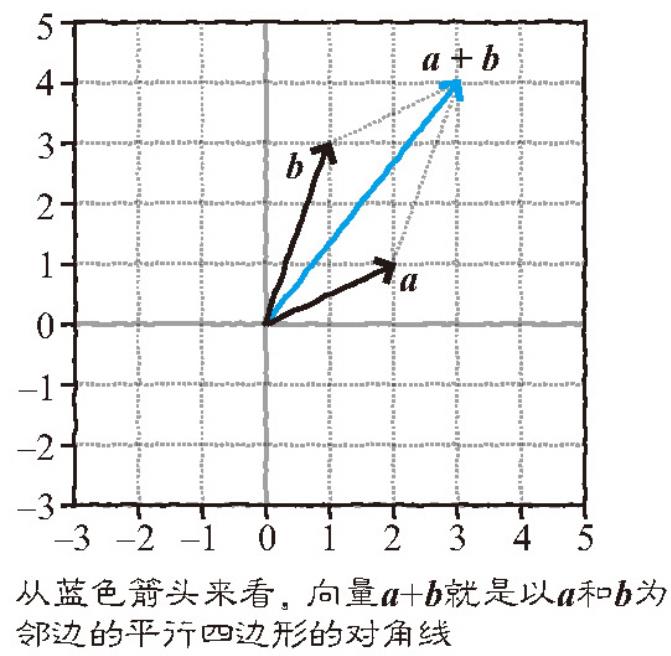
向量的加法运算可以通过图形解释。首先，将向量的元素看作坐标点，将向量看作一个从坐标原点开始，延伸到元素坐标点的箭头。这样一来，单纯地将各个元素相加的向量加法运算就可以看作，对以$$\begin{array}{r}\mathbf{a}和\mathbf{b}\end{array}$$为邻边的平行四边形求对角线。

示例代码：

import numpy as np
a = np.array([2, 1])
b = np.array([1, 3])
print(a + b)

向量的减法运算与加法运算相同，是对各个元素进行减法运算：
$$\begin{array}{r}\mathbf{a}-\mathbf{b}=\left[\begin{array}{c}2\\ 1\end{array}\right]-\left[\begin{array}{c}1\\ 3\end{array}\right]\end{array}=\left[\begin{array}{c}2-1\\ 1-3\end{array}\right]=\left[\begin{array}{c}1\\ -2\end{array}\right]$$
示例代码：

import numpy as np
a = np.array([2, 1])
b = np.array([1, 3])
print(a - b)

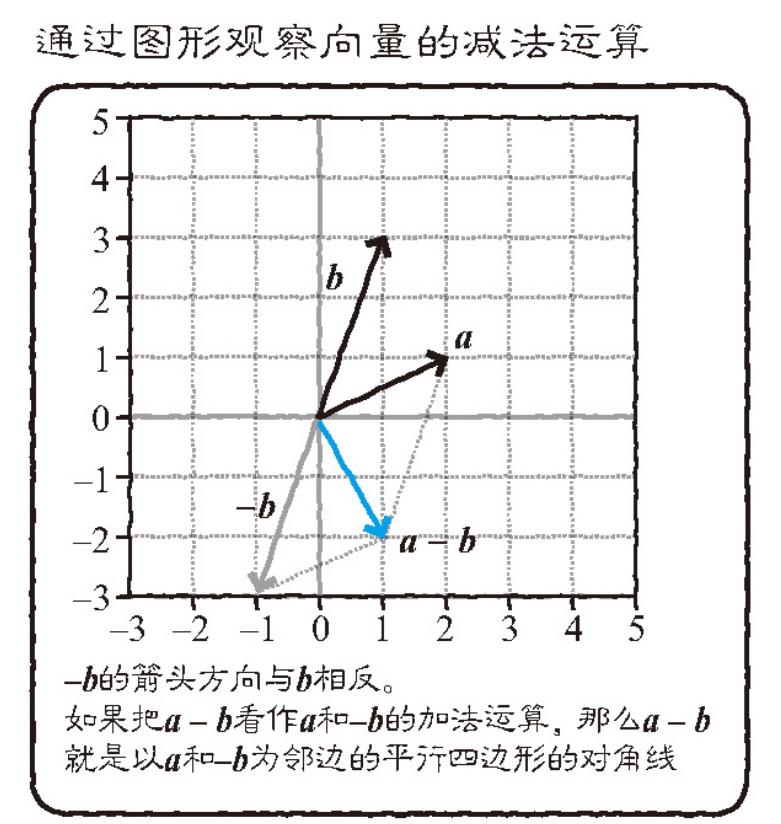
a - b 就是 a + (-b) ，可以看作 a 和 -b 的加法运算。从图形上来说， -b 的箭头方向与 b 相反。所以，a + (-b) 是以 a 和 -b 为邻边的平行四边形的对角线。

1.4 标量积

在标量与向量的乘法运算中，标量的值会与向量的各个元素分别相乘，比如 2a：
$$\begin{array}{r}2\mathbf{a}=2\times \left[\begin{array}{c}2\\ 1\end{array}\right]\end{array}=\left[\begin{array}{c}2\times 2\\ 2\times 1\end{array}\right]=\left[\begin{array}{c}4\\ 2\end{array}\right]$$
示例代码：

import numpy as np
a = np.array([2, 1])
print(2 * a)

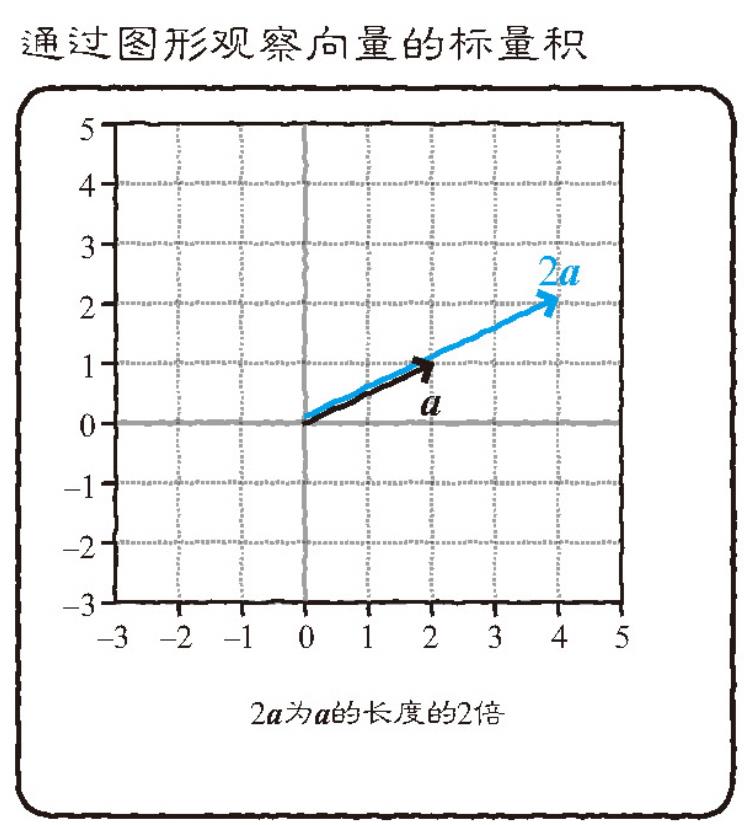
从图形上来说，向量的长度变成了标量倍，如下图所示：

1.5 内积

向量与向量之间的乘法运算叫作内积。内积是由相同维度的两个向量进行的运算，通常用 · 表示，这在机器学习涉及的数学中很常见。内积运算是把对应的元素相乘，然后求和，比如：
b = [ 1 3 ] ,