比特币白皮书-结论
Posted 哈希实验室
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了比特币白皮书-结论相关的知识,希望对你有一定的参考价值。
上一章,我们讨论了白皮书中的《比特币白皮书-计算》,这一章,我们来介绍比特币白皮书中的最后一部分-总结(Conclusion)。
原文:
We have proposed a system for electronic transactions without relying on trust. We started with the usual framework of coins made from digital signatures, which provides strong control of ownership, but is incomplete without a way to prevent double-spending. To solve this, we proposed a peer-to-peer network using proof-of-work to record a public history of transactions that quickly becomes computationally impractical for an attacker to change if honest nodes control a majority of CPU power. The network is robust in its unstructured simplicity. Nodes work all at once with little coordination. They do not need to be identified, since messages are not routed to any particular place and only need to be delivered on a best effort basis. Nodes can leave and rejoin the network at will, accepting the proof-of-work chain as proof of what happened while they were gone. They vote with their CPU power, expressing their acceptance of valid blocks by working on extending them and rejecting invalid blocks by refusing to work on them. Any needed rules and incentives can be enforced with this consensus mechanism.
翻译:
我们在此提出了一种不需要信用中介的电子支付系统。我们首先讨论了通常的电子货币的电子签名原理,虽然这种系统为所有权提供了强有力的控制,但是不足以防止双重支付。为了解决这个问题,我们提出了一种采用工作量证明机制的点对点网络来记录交易的公开信息,只要诚实的节点能够控制绝大多数的CPU计算能力,就能使得攻击者事实上难以改变交易记录。该网络的强健之处在于它结构上的简洁性。节点之间的工作大部分是彼此独立的,只需要很少的协同。每个节点都不需要明确自己的身份,由于交易信息的流动路径并无任何要求,所以只需要尽其最大努力传播即可。节点可以随时离开网络,而想重新加入网络也非常容易,因为只需要补充接收离开期间的工作量证明链条即可。节点通过自己的CPU计算力进行投票,表决他们对有效区块的确认,他们不断延长有效的区块链来表达自己的确认,并拒绝在无效的区块之后延长区块以表示拒绝。本框架包含了一个P2P电子货币系统所需要的全部规则和激励措施。
01 笔者总结
我们一起看过了白皮书中所有的内容,对于白皮书、中本聪、比特币,区块链,每个人都有自己的见解。
有人称中本聪是神,他赐予人们丰饶之角,让人们富有,也有人称中本聪是魔鬼,他亲手打开了潘多拉的盒子,让人倾家荡产、家破人亡,但无论如何,我们都应该虚心学习、接纳新事物,不要过急的定义新事物的好与坏,《比特币:一种点对点的电子现金系统》真的值得去仔细读一下,技术之全面,设计之精妙,值得赞叹。2019年10月24日,我国将区块链作为新兴数字产业之一,我相信在不久之后,区块链将像如今的互联网一样影响每个人。
02 是结束也是开始
比特币白皮书部分已经介绍完了,接下来,笔者将会带大家一起学习更多的区块链知识,一起努力吧!
期待您的点评、分享、关注、在看,您的鼓励是我写作的最大动力!PEACE !
参考文献:
《Bitcoin: A Peer-to-Peer Electronic Cash System》
https://bitcoin.org/bitcoin.pdf
《比特币白皮书:一种点对点的电子现金系统》
https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system
比特币白皮书-计算
上一章,我们讨论了白皮书中的《比特币白皮书-隐私》,这一章,我们来介绍比特币白皮书中的计算(Calculations)。
原文:
We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain. Even if this is accomplished, it does not throw the system open to arbitrary changes, such as creating value out of thin air or taking money that never belonged to the attacker. Nodes are not going to accept an invalid transaction as payment, and honest nodes will never accept a block containing them. An attacker can only try to change one of his own transactions to take back money he recently spent.
The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk. The success event is the honest chain being extended by one block, increasing its lead by +1, and the failure event is the attacker\'s chain being extended by one block, reducing the gap by -1.
The probability of an attacker catching up from a given deficit is analogous to a Gambler\'s Ruin problem. Suppose a gambler with unlimited credit starts at a deficit and plays potentially an infinite number of trials to try to reach breakeven. We can calculate the probability he ever reaches breakeven, or that an attacker ever catches up with the honest chain, as follows [8]:
p = probability an honest node finds the next block
q = probability the attacker finds the next block
qz = probability the attacker will ever catch up from z blocks behind
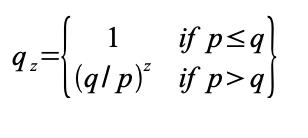
Given our assumption that p > q, the probability drops exponentially as the number of blocks the attacker has to catch up with increases. With the odds against him, if he doesn\'t make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind.
We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can\'t change the transaction. We assume the sender is an attacker who wants to make the recipient believe he paid him for a while, then switch it to pay back to himself after some time has passed.
The receiver will be alerted when that happens, but the sender hopes it will be too late. The receiver generates a new key pair and gives the public key to the sender shortly before signing. This prevents the sender from preparing a chain of blocks ahead of time by working on it continuously until he is lucky enough to get far enough ahead, then executing the transaction at that moment. Once the transaction is sent, the dishonest sender starts working in secret on a parallel chain containing an alternate version of his transaction.
The recipient waits until the transaction has been added to a block and z blocks have been linked after it. He doesn\'t know the exact amount of progress the attacker has made, but assuming the honest blocks took the average expected time per block, the attacker\'s potential progress will be a Poisson distribution with expected value:
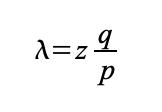
To get the probability the attacker could still catch up now, we multiply the Poisson density for each amount of progress he could have made by the probability he could catch up from that point:
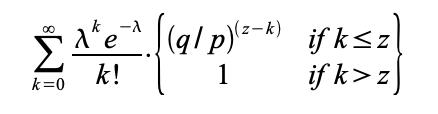
Rearranging to avoid summing the infinite tail of the distribution...

Converting to C code...
#include <math.h>
double AttackerSuccessProbability(double q, int z)
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
return sum;
Running some results, we can see the probability drop off exponentially with z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
Solving for P less than 0.1%...
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
翻译:
设想如下场景:一个攻击者试图比诚实节点产生链条更快地制造替代性区块链。即便它达到了这一目的,但是整个系统也并非就此完全受制于攻击者的独断意志了,比方说凭空创造价值,或者掠夺本不属于攻击者的货币。这是因为节点将不会接受无效的交易,而诚实的节点永远不会接受一个包含了无效信息的区块。一个攻击者能做的,最多是更改他自己的交易信息,并试图拿回他刚刚付给别人的钱。诚实链条和攻击者链条之间的竞赛,可以用二叉树随机漫步(Binomial Random Walk)来描述。成功事件定义为诚实链条延长了一个区块,使其领先性+1,而失败事件则是攻击者的链条被延长了一个区块,使得差距-1。攻击者成功填补某一既定差距的可能性,可以近似地看做赌徒破产问题(Gambler’s Ruin problem)。假定一个赌徒拥有无限的透支信用,然后开始进行潜在次数为无穷的赌博,试图填补上自己的亏空。那么我们可以计算他填补上亏空的概率,也就是该攻击者赶上诚实链条,如下所示

假定p>q,那么攻击成功的概率就因为区块数的增长而呈现指数化下降。由于概率是攻击者的敌人,如果他不能幸运且快速地获得成功,那么他获得成功的机会随着时间的流逝就变得愈发渺茫。那么我们考虑一个收款人需要等待多长时间,才能足够确信付款人已经难以更改交易了。我们假设付款人是一个支付攻击者,希望让收款人在一段时间内相信他已经付过款了,然后立即将支付的款项重新支付给自己。虽然收款人届时会发现这一点,但为时已晚。收款人生成了新的一对密钥组合,然后只预留一个较短的时间将公钥发送给付款人。这将可以防止以下情况:付款人预先准备好一个区块链然后持续地对此区块进行运算,直到运气让他的区块链超越了诚实链条,方才立即执行支付。当此情形,只要交易一旦发出,攻击者就开始秘密地准备一条包含了该交易替代版本的平行链条。然后收款人将等待交易出现在首个区块中,然后在等到z个区块链接其后。此时,他仍然不能确切知道攻击者已经进展了多少个区块,但是假设诚实区块将耗费平均预期时间以产生一个区块,那么攻击者的潜在进展就是一个泊松分布,分布的期望值为:
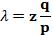
当此情形,为了计算攻击者追赶上的概率,我们将攻击者取得进展区块数量的泊松分布的概率密度,乘以在该数量下攻击者依然能够追赶上的概率。
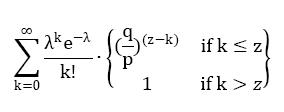
化为如下形式,避免对无限数列求和:
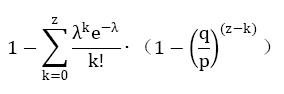
写为如下C语言代码:
#include <math.h>
double AttackerSuccessProbability(double q, int z)
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
return sum;
结果,发现概率对z值呈指数下降。
当q=0.1时
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
当q=0.3时
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
求解令P<0.1%的z值:
为使P<0.001
则q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
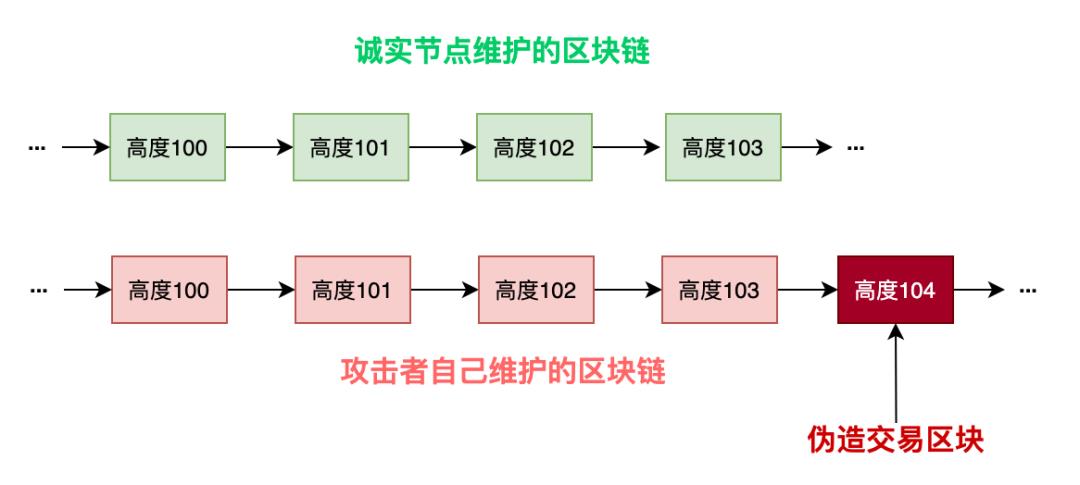
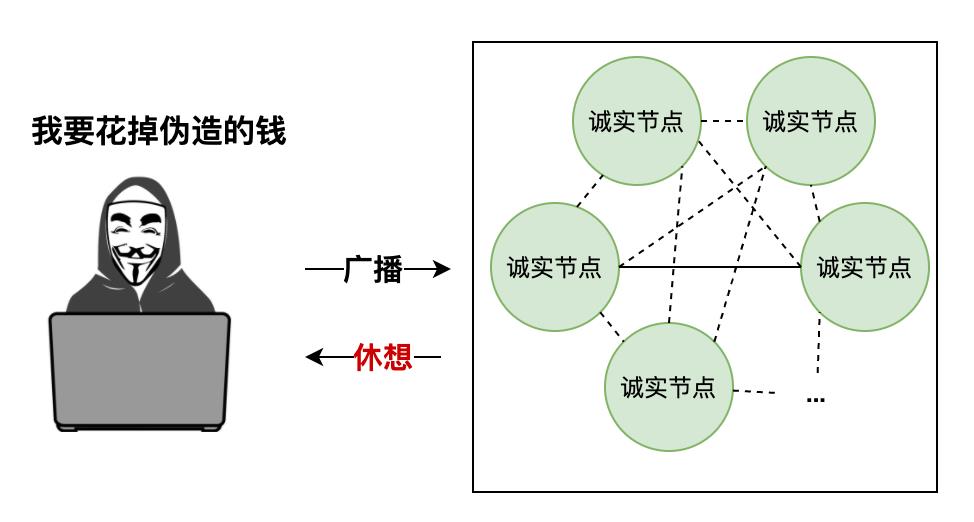
01 攻击者的伪造
如果攻击者制造了一条区块链,该区块链比目前正在运行的区块链(诚实节点制造的链)速度更快,他完全可以伪造交易,比如从某某地址转账给自己,并且记录在自己制造的区块链上,但这只能是自己玩玩,因为,该交易不存在有效的上一笔交易,因此,该交易是无效的,钱也不会被诚实节点认可,因此攻击者花时间伪造区块交易是无意义的。
02 什么是泊松分布
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布,比如机器出现的故障数。假设每产生一个诚实的区块耗费时间符合预期值,则说明攻击者的行为也符合泊松分布。
03 为什么总说等6次确认
我们经常会说,比特币网络上要等待6次确认之后,才可以说转账成功,白皮书给了我们很好的解释:
诚实节点出块的概率 + 攻击者出块的概率 = 1
攻击者如果想追上诚实节点链的概率与以下因素有关:
攻击者落后于诚实节点链的距离攻击者出块的概率
因此,攻击者只能从这两个方面攻击。
根据白皮书中的数据,我们可以得出3个参数
z=攻击者落后于诚实节点链的距离
q=攻击者出块的概率
P=攻击者追上诚实节点的概率
当攻击者出块的概率(q)固定时,攻击者落后于诚实节点链的距离(z) 越大,攻击者追上诚实节点的概率(P)越小
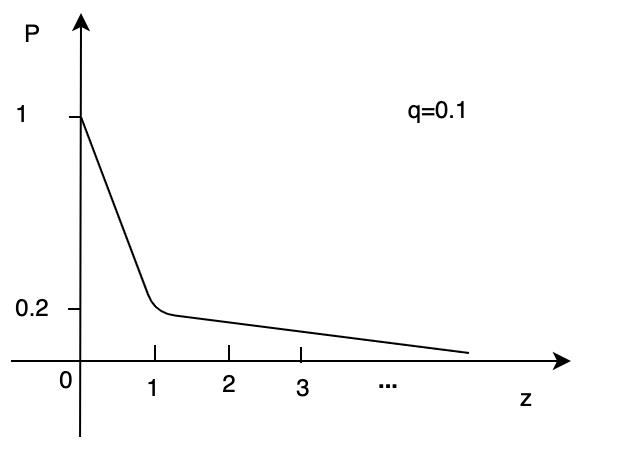
当攻击者出块的概率q=0.3时,说明攻击者的算力增强,但是随着攻击者落后于诚实节点链的距离(z) 增大,攻击者追上诚实节点的概率(P)也在呈指数递减。
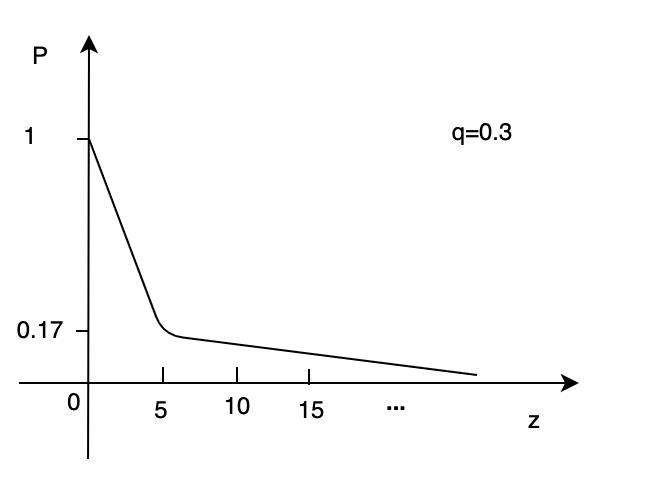
白皮书中还指出:
如果想让攻击者追上诚实节点的概率(P)值维持在0.1%以下,如果攻击者出块的概率(q)是10%,攻击者落后于诚实节点链的距离(z)等于5就可以了。

因此,为什么说比特币网络上要等待6次确认之后,才可以说转账成功,因为达到6个确认之后,攻击者追上诚实节点的概率就非常小了。
但是如果攻击者制造下个区块的概率大于诚实节点制造下个区块的概率,则要考虑51%的攻击了,这是另一个话题。
期待您的点评、分享、关注、在看,您的鼓励是我写作的最大动力!PEACE !
这一章,我们来介绍比特币白皮书中计算(Calculations),下一章,我们将介绍比特币白皮书中最后一部分-结论(Conclusion)。
参考文献:
《Bitcoin: A Peer-to-Peer Electronic Cash System》
https://bitcoin.org/bitcoin.pdf
《比特币白皮书:一种点对点的电子现金系统》
https://www.8btc.com/wiki/bitcoin-a-peer-to-peer-electronic-cash-system
《泊松分布》
https://zh.wikipedia.org/wiki/%E5%8D%9C%E7%93%A6%E6%9D%BE%E5%88%86%E5%B8%83
以上是关于比特币白皮书-结论的主要内容,如果未能解决你的问题,请参考以下文章