树链剖分
Posted $huge{color {#66CCFF} {GYC}}$
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树链剖分相关的知识,希望对你有一定的参考价值。
板子:P3384
查错查的心态都炸了
前言
链剖分:指对数的边进行划分的一类操作,目的是减少在链上修改、查询等操作的复杂度
树链剖分有三类:轻重链剖分、虚实剖分和长链剖分
而今天我要讲的是轻重链剖分
思想
通过轻重链剖分将树分成多条链,保证每个节点都只属于一条链
\\(\\color{#66ccff} {1重儿子}\\)
节点\\(x\\)的子节点中,包含子节点数目最多的子节点为该节点的重儿子
\\(\\color{#39c5bb} {2轻儿子}\\)
节点\\(x\\)的字节点中,除了重儿子,其余都是轻儿子
\\(\\color{#66ccff} {3重链}\\)
节点到重儿子之间的路径为重链,每条重链相当于一个区间,把所有重链首尾相接组成一个线性节点序列,再通过数据结构维护即可(相邻重边连起来的 连接一条重儿子 的链叫重链)
\\(\\color{#39c5bb} {4轻链}\\)
同上
\\(\\color{#66ccff} {5重边}\\)
连接该节点与它的重儿子的边
\\(\\color{#39c5bb} {6轻边}\\)
同上
例:
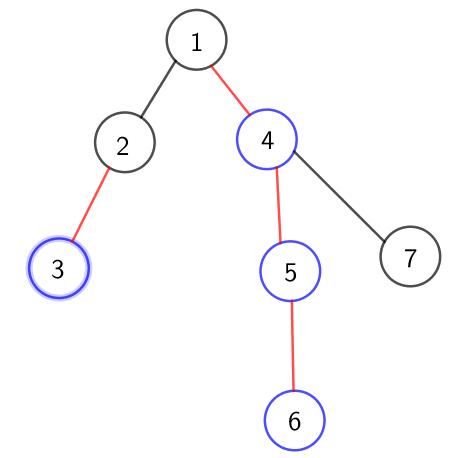
蓝色为重儿子,红色为重边———图转自作者
前置
#include<bits/stdc++.h>
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define len (r-l+1)
#define N 200010
using namespace std;
int n,m,r,p;
int tot,first[N],nex[N],to[N],w[N],wt[N];//w[]、wt[]初始点权数组+邻接表
int a[N<<2],laz[N<<2];//线段树+懒标
int son[N],id[N],fa[N],cnt,dep[N],siz[N],top[N];//son[]重儿子编号,id[]新编号,fa[]父亲节点,cnt dfs_clock/dfs序,dep[]深度,siz[]子树大小,top[]当前链顶端节点
int res=0;//查询答案
预处理
注意:先处理重儿子,再处理轻儿子!
因为顺序是先重再轻,所以每一条重链的新编号是连续的
因为是dfs,所以每一个子树的新编号也是连续的
完成重链与轻链的处理
分别是\\(\\color{red}{df1}和\\color{green} {dfs2}\\)
\\(\\huge {dfs1:}\\)
inline void dfs1(int x,int f,int deep){//x当前节点,f父亲,deep深度
dep[x]=deep;
fa[x]=f;
siz[x]=1;
int maxson=-1;
for(int i=first[x];i;i=nex[i]){
int y=to[i];
if(y==f) continue;
dfs1(y,x,deep+1);
siz[x]+=siz[y];
if(siz[y]>maxson) son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号
}
}
\\(\\huge {dfs2}\\):
inline void dfs2(int x,int topf){////x当前节点,topf当前链的最顶端的节点
id[x]=++cnt;//标记每个点的新编号
wt[cnt]=w[x];//把每个点的初始值赋到新编号上来
top[x]=topf;
if(!son[x]) return ;//先处理重儿子,在处理轻儿子--因为根据设置的编号要使得整棵树最后连续
dfs2(son[x],topf);
for(int i=first[x];i;i=nex[i]){
int y=to[i];
if(y==fa[x]||y==son[x]) continue;
dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链
}
}
然后建立线段树
//======================线段树======================
inline void pushdown(int rt,int lenn){
laz[rt<<1]+=laz[rt];
laz[rt<<1|1]+=laz[rt];
a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
a[rt<<1|1]+=laz[rt]*(lenn>>1);
a[rt<<1]%=p;
a[rt<<1|1]%=p;
laz[rt]=0;
}
inline void build(int rt,int l,int r){
if(l==r){
a[rt]=wt[l];
if(a[rt]>p) a[rt]%=p;
return ;
}
build(lson);
build(rson);
a[rt]=(a[rt<<1]+a[rt<<1|1])%p;
}
inline void update(int rt,int l,int r,int L,int R,int z){
if(L<=l&&r<=R){
laz[rt]+=z;
a[rt]+=z*len;
}
else{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) update(lson,L,R,z);
if(R>mid) update(rson,L,R,z);
a[rt]=(a[rt<<1]+a[rt<<1|1])%p;
}
}
inline void query(int rt,int l,int r,int L,int R){
if(L<=l&&r<=R){
res+=a[rt];
res%=p;
return ;
}
else{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) query(lson,L,R);
if(R>mid) query(rson,L,R);
}
}
不同的操作
1:区间更新
inline void updRange(int x,int y,int z){
z%=p;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
update(1,1,n,id[top[x]],id[x],z);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
update(1,1,n,id[x],id[y],z);
}
1:如果\\(u\\)和\\(v\\)在同一条重链上,则在线段树上查询其对应的下标区间id[u]到id[v]
2:反之,则一边查询,一边将u和v向同一条重链上移,再处理
2区间查询
inline int qRange(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
res=0;
query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
ans+=res;
ans%=p;
x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
}//直到两个点处于一条链上
if(dep[x]>dep[y])swap(x,y);//保证x的深度更大
res=0;
query(1,1,n,id[x],id[y]);
ans+=res;
return ans%p;
}
3单点更新和修改
区间id[x]到id[x]+siz[x]-1全部都要更新和查询
inline void updSon(int x,int y){
update(1,1,n,id[x],id[x]+siz[x]-1,y);
}
inline int qSon(int x){
res=0;
query(1,1,n,id[x],id[x]+siz[x]-1);
return res;
}
线段树
//======================线段树======================
inline void pushdown(int rt,int lenn){
laz[rt<<1]+=laz[rt];
laz[rt<<1|1]+=laz[rt];
a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
a[rt<<1|1]+=laz[rt]*(lenn>>1);
a[rt<<1]%=p;
a[rt<<1|1]%=p;
laz[rt]=0;
}
inline void build(int rt,int l,int r){
if(l==r){
a[rt]=wt[l];
if(a[rt]>p) a[rt]%=p;
return ;
}
build(lson);
build(rson);
a[rt]=(a[rt<<1]+a[rt<<1|1])%p;
}
inline void update(int rt,int l,int r,int L,int R,int z){
if(L<=l&&r<=R){
laz[rt]+=z;
a[rt]+=z*len;
}
else{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) update(lson,L,R,z);
if(R>mid) update(rson,L,R,z);
a[rt]=(a[rt<<1]+a[rt<<1|1])%p;
}
}
inline void query(int rt,int l,int r,int L,int R){
if(L<=l&&r<=R){
res+=a[rt];
res%=p;
return ;
}
else{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) query(lson,L,R);
if(R>mid) query(rson,L,R);
}
}
总代码:
#include<bits/stdc++.h>
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define len (r-l+1)
#define N 200010
using namespace std;
int n,m,r,p;
int tot,first[N],nex[N],to[N],w[N],wt[N];//w[]、wt[]初始点权数组
int a[N<<2],laz[N<<2];
int son[N],id[N],fa[N],cnt,dep[N],siz[N],top[N];//son[]重儿子编号,id[]新编号,fa[]父亲节点,cnt dfs_clock/dfs序,dep[]深度,siz[]子树大小,top[]当前链顶端节点
int res=0;//查询答案
//======================快读========================
inline int read(){
int p=0,f=1;
char c=getchar();
while(!isdigit(c)){if(c==\'-\')f=-1;c=getchar();}
while(isdigit(c)){p=p*10+c-\'0\';c=getchar();}
return p*f;
}
//====================邻接表========================
inline void add(int x,int y){//链式前向星加边
to[++tot]=y;
nex[tot]=first[x];
first[x]=tot;
}
//===================初始化=========================
inline void dfs1(int x,int f,int deep){//x当前节点,f父亲,deep深度
dep[x]=deep;
fa[x]=f;
siz[x]=1;
int maxson=-1;
for(int i=first[x];i;i=nex[i]){
int y=to[i];
if(y==f) continue;
dfs1(y,x,deep+1);
siz[x]+=siz[y];
if(siz[y]>maxson) son[x]=y,maxson=siz[y];//标记每个非叶子节点的重儿子编号
}
}
inline void dfs2(int x,int topf){////x当前节点,topf当前链的最顶端的节点
id[x]=++cnt;//标记每个点的新编号
wt[cnt]=w[x];//把每个点的初始值赋到新编号上来
top[x]=topf;
if(!son[x]) return ;
dfs2(son[x],topf);
for(int i=first[x];i;i=nex[i]){
int y=to[i];
if(y==fa[x]||y==son[x]) continue;
dfs2(y,y);//对于每一个轻儿子都有一条从它自己开始的链
}
}
//======================线段树======================
inline void pushdown(int rt,int lenn){
laz[rt<<1]+=laz[rt];
laz[rt<<1|1]+=laz[rt];
a[rt<<1]+=laz[rt]*(lenn-(lenn>>1));
a[rt<<1|1]+=laz[rt]*(lenn>>1);
a[rt<<1]%=p;
a[rt<<1|1]%=p;
laz[rt]=0;
}
inline void build(int rt,int l,int r){
if(l==r){
a[rt]=wt[l];
if(a[rt]>p) a[rt]%=p;
return ;
}
build(lson);
build(rson);
a[rt]=(a[rt<<1]+a[rt<<1|1])%p;
}
inline void update(int rt,int l,int r,int L,int R,int z){
if(L<=l&&r<=R){
laz[rt]+=z;
a[rt]+=z*len;
}
else{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) update(lson,L,R,z);
if(R>mid) update(rson,L,R,z);
a[rt]=(a[rt<<1]+a[rt<<1|1])%p;
}
}
inline void query(int rt,int l,int r,int L,int R){
if(L<=l&&r<=R){
res+=a[rt];
res%=p;
return ;
}
else{
if(laz[rt]) pushdown(rt,len);
if(L<=mid) query(lson,L,R);
if(R>mid) query(rson,L,R);
}
}
//======================操作========================
inline void updRange(int x,int y,int z){
z%=p;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
update(1,1,n,id[top[x]],id[x],z);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
update(1,1,n,id[x],id[y],z);
}
inline int qRange(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
res=0;
query(1,1,n,id[top[x]],id[x]);//ans加上x点到x所在链顶端 这一段区间的点权和
ans+=res;
ans%=p;
x=fa[top[x]];//把x跳到x所在链顶端的那个点的上面一个点
}//直到两个点处于一条链上
if(dep[x]>dep[y])swap(x,y);//保证x的深度更大
res=0;
query(1,1,n,id[x],id[y]);
ans+=res;
return ans%p;
}
inline void updSon(int x,int y){
update(1,1,n,id[x],id[x]+siz[x]-1,y);
}
inline int qSon(int x){
res=0;
query(1,1,n,id[x],id[x]+siz[x]-1);
return res;
}
//======================主函数======================
int main(){
n=read(),m=read(),r=read(),p=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<n;i++){
int a,b;
a=read();b=read();
add(a,b);add(b,a);
}
dfs1(r,0,1);
dfs2(r,r);
build(1,1,n);
while(m--){
int k,x,y,z;
k=read();
if(k==1){
x=read(),y=read(),z=read();
updRange(x,y,z);
}
else if(k==2){
x=read(),y=read();
cout<<qRange(x,y)<<endl;
}
else if(k==3){
x=read(),y=read();
updSon(x,y);
}
else{
x=read();
cout<<qSon(x)<<endl;
}
}
return 0;
}
总结
通过对树进行划分,得到一个新的区间,由线段树进行维护,可以降低操作的时间复杂度
树链剖分详解
食用之前请务必搞清楚线段树
什么是树链剖分
- 树链剖分,它可以对一棵树进行轻重链剖分后用数据结构来维护每条重链。
- 比如下面这个问题:假设每个点有一个点权。如何把一棵树上的两个点\(u\),\(v\)之间的简单路径上的所有点的点权增加\(d\)?
- 这就是树链剖分能够解决的的一个基本问题。
接下来介绍一下树链剖分的详细过程。
轻重链剖分
树链剖分的第一步就是将一棵树进行轻重链剖分。这一步决定了整个树链剖分的时间复杂度。
引入几个概念:
- \(size[u]\):以\(u\)为根的子树大小
- \(wson[u]\):在\(u\)的儿子中\(size\)值最大的那一个,称作\(u\)的重儿子
- \(dfn[u]\):每个点的dfs序号。\(pre[tot]\),如果dfn[u]=tot,则\(pre[tot]=u\)
- 重链:指每个点与它的重儿子之间的连边(\(u\)---\(wson[u]\))
轻链:在所有边中不是重的其他边
举个例子来详细说一下。
- 如上图
(一张从百度百科挖来的图),每一个带红点的点就是轻儿子;每一条加粗的的边就是重链,没有加粗的就是轻边。比如说对于点2,那么
\(wson[2]=6,size[2]=5,size[wson[u]]=size[6]=3\)。 - \(dfn[u]\)的含义就要稍微的特殊一些。因为它不仅仅是简单的dfs序号,而是按照轻重链的顺序来定义的。每次从一个点\(u\)往下dfs的时候,优先对\(wson[u]\)进行dfs,然后再遍历轻儿子们。
- 比如说上图,每条边上有一个序号。把这个序号看做是点的(比如说1->4上面的1应该是dfn[4])。从1开始dfs,可以明显的看到是先对4进行dfs,然后再对wson[4]也就是9进行dfs....到了叶子节点再回溯去dfs轻儿子。
- 为什么要这样做呢?因为这样之后,可以看到,每一条长重链上的每个点的dfn是连续的。比如1->4->9->13->14这条长重链上的dfn便是连续的,其他两条也一样。这样一来,就可以用维护区间的数据结构(比如线段树)来维护重链上的信息。
树链剖分的好处
- 一个上面已经说了,就是重链上的dfn是连续的,可以用数据结构维护
还有就是,在每一条由根到叶子结点的路径上,轻链的条数和重链的长度均不会超过\(\log n\)。这个性质决定了树链剖分的时间复杂度。如果是拿线段树来维护链的话,复杂度就是\(n \log^2n\)
代码实现轻重链剖分
- 一共需要两个dfs。
第一个用来处理每个点的基础信息(\(wson,size,dep,fa\))
第一个dfs代码:
inline dfs1(int u, int f)//两个参数:u是现在的点,f是u的父亲
{
size[u] = 1;//最开始u的子树中只有u一个点
for(edge *p = head[u]; p; p = p->next)//遍历每一个与u相连的点
{
int v = p->v;
if(v == f) continue;//如果此点是u的父亲就跳过
dep[v] = dep[u] + 1;
fa[v] = u;//处理信息
dfs1(v, u);//继续递归
size[u] += size[v];//u的子树大小要加上v的子树大小
if(size[wson[u]] < size[v]) wson[u] = v;//更新重儿子
}
}- 这样就用一个dfs处理出了每个点的信息。
- 再用第二个dfs求出每个点的dfn以及该点所处的链的链首。
代码:
inline void dfs2(int u, int tp)//u是当前点,tp是该链链首
{
dfn[u] = ++tot, pre[tot] = u, top[u] = tp;
//pre是dfn的反函数。如dfn[2] = 3,pre[3] = 2...
//为什么要有这个反函数,因为在建线段树的时候是用dfn建的,然而如果想要知道原来那个点的信息就要知道pre
if(wson[u]) dfs2(wson[u], tp);//有重子就继续往下拉重链
for(edge * p = head[u]; p; p = p->next)//回过头来在轻儿子中拉链
{
int v = p->v;
if(v != fa[u] && v != wson[u]) dfs2(v, v);//如果不是爸爸或重儿子,已该点为链首继续拉链
}
}至此,轻重链剖分完成,然后便是第二大块——
线段树维护重链
- 就是用线段树维护重链上的信息。
- 注意事项:这里所有的参数都是以dfn的形象出现的,而不是原来那个点的序号。
inline void build(node *r, int left, int right)
{
r->left = left, r->right = right, r->lazy = -1, r->s = 0;
if(left == right)
{
r->s = value[pre[left]];
//这里是pre[left]不是left!原因就是刚才说的:这里所有的参数都是以dfn的形象出现的,而不是原来那个点的序号。
return ;
}
int mid = (left + right) / 2;
node *lson = &pool[++cnt], *rson = &pool[++cnt];
r->ch[0] = lson, r->ch[1] = rson;
build(lson, left, mid); build(rson, mid + 1, right);
pushup(r);
}基础的查询修改操作(在重链上的)就是原来的函数,怎么写详细请看线段树基础。
最后一步,也就是——
两点间路径的修改&查询
- 就是最开始提到的问题:如何把一棵树上的两个点\(u\),\(v\)之间的简单路径上的所有点的点权增加\(d\)?
上图
Q1:如果想要求11与2之间的和该怎样?
A1:在同一重链上,直接调用query查询就行了。
- 在同一重链上的两点都可以直接查询
Q2:求6与7之间的和?
A2:将6跳到1,同时答案加上query(dfn[2],dfn[6]);然后将7跳到1,答案加上query(dfn[3],dfn[7])
- 在不同重链上的两个点就一直按重链向上跳,直到跳到同一条重链上--->Q1
代码(修改的):
inline void modify(int u, int v, int d)
{
while(top[u] != top[v]) //直到跳到一条链上
{
if(dfn[top[u]] < dfn[top[v]]) swap(u, v);//这里根据链首的值交换一下
change(root, dfn[top[u]], dfn[u], d), u = fa[top[u]];//最后u=链首的爸爸
}
if(dep[u] > dep[v]) swap(u, v);
change(root, dfn[u], dfn[v], d);
//Q1
}查询的(基本类似):
inline int Qsum(int u, int v)
{
int ret = 0;
while(top[u] != top[v])
{
if(dfn[top[u]] < dfn[top[v]]) swap(u, v);
ret += query(root, dfn[top[u]], dfn[u]), u = fa[top[u]];
}
if(dep[u] > dep[v]) swap(u, v);
ret += query(root, dfn[u], dfn[v]);
return ret;
}至此基本完结
类模板题
CF343D,[NOI2015]软件包管理器,[SHOI2012]魔法树,[SDOI2011]染色,[ZJOI2008]树的统计
以上是关于树链剖分的主要内容,如果未能解决你的问题,请参考以下文章

