CF1592C Bakry and Partitioning | 异或

Posted 2021-11-12 ltdJcoder

不难的异或思维题

传送门

题意

给定一颗大小为\\(n\\)带点权的树, 和一个整数\\(k\\)
询问是否可以删除至多\\(k-1\\)条边（至少1条）， 将树分成至多\\(k\\)个连通块，使得每个连通块中的点权异或和相同

题解

这种题的思路大概就是考虑分成很多连通块时， 是否能用较少的联通块等效代替

容易想到， 如果划分成\\(m\\)个异或和相同的联通块，当\\(m\\)为偶数，肯定也能分成两个异或和为0的连通块，
同理， \\(m\\)为奇数， 也能分成3个相同的连通块

也就是，要么两个， 要么三个， 分类讨论嘛：

---

1. 两个的话简单， 肯定将原树和他的一颗子树分开
   枚举子树即可

2. 三个的话， 也就是说， 我们要将原树的两颗子树分离开
   那么继续讨论， 两颗子树是否相交：
   

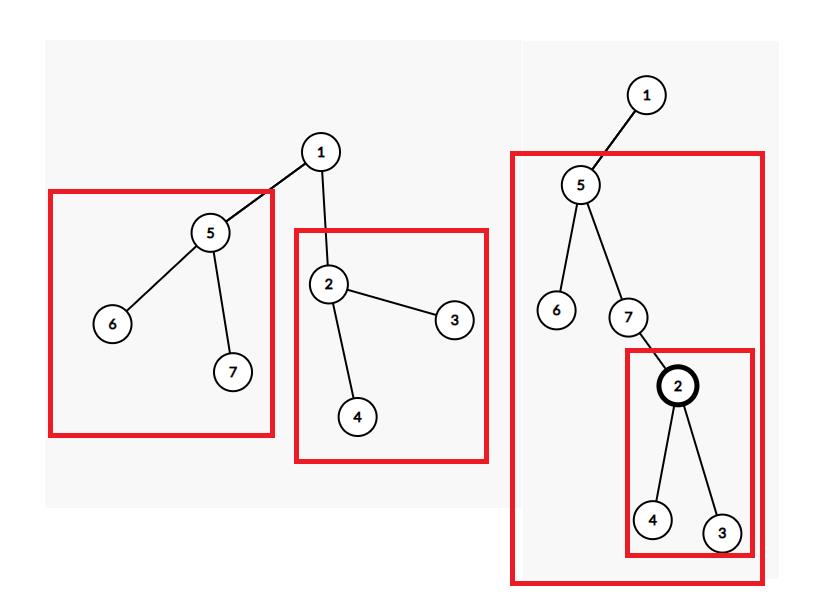
如果不相交的话， 我们假设三颗子树的异或和分别为： \\(a, b, c\\)
显然：要满足 \\(a \\oplus (b \\oplus c) = b = c\\)
因为\\(b = c\\)得到 \\(b \\oplus c = 0\\)
所以\\(a = b = c\\)
统计是否存在即可

如果相交的话， 显然： \\(a \\oplus b = b \\oplus c = c\\)
得到\\(a = c , b = 0\\)
依然统计即可

因为a一定为根节点， 上面两个不难统计

#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;

int read(){
    int num=0, flag=1; char c=getchar();
    while(!isdigit(c) && c!=\'-\') c=getchar();
    if(c == \'-\') c=getchar(), flag=-1;
    while(isdigit(c)) num=num*10+c-\'0\', c=getchar();
    return num*flag;
}

const int N = 290005;
int T, n;
int A[N], sum[N], a[N], cnt[N], fa[N];
vector<int> p[N];

int flag;
int rflag = 0;

void dp(int x){
    sum[x] = a[x];
    for(auto nex : p[x]) {
        if(nex == fa[x]) continue;
        fa[nex] = x;
        dp(nex);
        sum[x] ^= sum[nex];
    }
}

void dfs(int x){
    int res = 0;
    for(auto nex : p[x]){
        if(nex == fa[x]) continue;
        dfs(nex);
        if(cnt[nex]) res++;
        if(cnt[nex] && sum[x]==0) rflag=1; 
    }
    if(res >= 2) rflag = 1;
    if(sum[x] == sum[1] || res) cnt[x]=1; 
}

int main(){
    T = read();
    while(T--){
        n = read(); int k=read();
        for(int i=1; i<=n; i++) {
            sum[i] = 0;
            cnt[i] = 0;
            p[i].clear();
            a[i] = read();
        }

        for(int i=1; i<n; i++){
            int u=read(), v=read();
            p[u].push_back(v);
            p[v].push_back(u);
        }

        flag = 0; rflag=0;
        dp(1);	
        for(int i=2; i<=n; i++){
            if((sum[1]^sum[i]) == sum[i]) flag=1;
        }

        if(!flag && k>=3){
            dfs(1);
            flag = rflag;
        }

        printf(flag?"YES\\n":"NO\\n");
    }
    return 0;
}

Codeforces Round #746 (Div. 2) C. Bakry and Partitioning

本文首发于微信公众号："算法与编程之美"，欢迎关注，及时了解更多此系列文章。

前言

题目来源 ：Codeforces Round#746 (Div. 2)

链接Codeforces : 

https://codeforces.com/contest/1592/problem/C

Bakry面临一个问题，但由于他懒得解决，他请求你的帮助。给你一棵有n个节点的树，第i个节点在1到n中的每一个i上都有分配给它的值ai。你想从树上删除至少1条，但最多k-1条边，这样下面的条件就成立了。对于每一个连接的组件，计算其中的节点值的位素XOR。然后，这些值对所有的连接部件都必须是相同的。

有没有可能达到这个条件呢？

输入：

每个测试包含多个测试案例。第一行包含测试用例的数量t（1≤t≤5⋅104）。测试用例的描述如下。

每个测试用例的第一行包含两个整数n和k（2≤k≤n≤105）。

每个测试用例的第二行包含n个整数a1,a2,...,an（1≤ai≤109）。

接下来n-1行的第i行包含两个整数ui和vi（1≤ui,vi≤n, ui≠vi），这意味着节点ui和vi之间有一条边。可以保证给定的图是一棵树。保证所有测试案例的n之和不超过2⋅105。

输出：

对于每个测试用例，你应该输出一个单一的字符串。如果你能根据上面写的条件删除边，则输出 "YES"（不带引号）。否则，输出"NO"（不带引号）。

你可以将 "YES "和 "NO "的每个字母以任何形式（大写或小写）打印出来。

样例

输入：

1

5 3

1 6 4 1 2

1 2

2 3

1 4

4 5

输出：

YES

问题描述

理解题意：该题题意大概是，能否通过至少1次、最多k-1次的删除操作，将给出的无向连通图G的边每次删除一条，使得删除后所组成的每组节点的异或值相等。（按照样例所示数据进行如下图分析）

提示：第一个图圆上的数字代表的是节点的编号，第二个图圆上的数字代表的是对应编号节点的节点值。

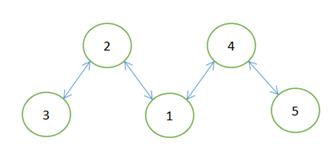
由题意可知若要解决此题必须了解异或操作的性质！

异或操作的性质：任意两个相等的值，异或操作后其值为零，即记x, y, 若x = y, 那么x ^ y = 0; 0与x的异或值为x, 记0 ^ x = x;

题意是要让分割后的每一部分异或值相等，所以可以根据异或的性质将其划分为两种情况：

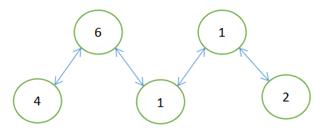
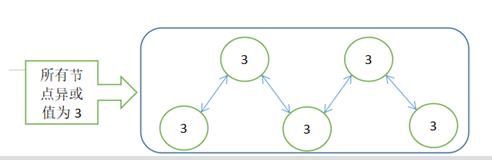
1、当满足所有节点值求异或后等于0，那么该情况一定可以划分为2个相等的部分进行异或操作，故满足题意；（如下图，所有节点的异或值为0）

当异或操作进行的最后一步时，一定是2剩余两部分异或值相同才能得到最终异或值为0；删除红叉的那条边，最终两部分的异或值相等。

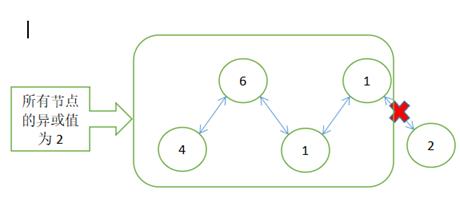
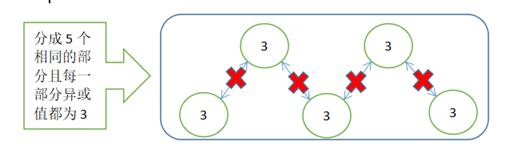
2、当所有节点值求异或后不等于0时，如下图所有节点的异或值为3，如果可以找出能将其划分为至少3部分，且每一部分的异或值都等于3时，那么也是满足题意的。

证明：我们可以这样来想，若最终的异或值最终为w, 那么若要满足题意，一定存在偶数组异或值相同且为w的部分，使得前面所有分割部分的异或值为0，才会使最终异或值为w.

最终分割结果

解决方案

有了以上问题的分析，可以很快得到解题思路；首先将所有节点的异或值w求出，判断其是否为w = 0，为0输出YES，反之进行上述第二种情况的判断；能否找出满足将其划分为至少3部分，且每一部分的异或值都等于w, 在此处可以采用dfs + 贪心进行判断;

具体操作：在回溯的过程中，会返回当前节点分支的异或值，若当前节点某个分支的异或值等于w时，我们可以贪心的将其边删除，该节点的余下分支(异或值不等于w的分支)再与该节点进行异或操作，每次贪心的删除一条边，我们就记录下来(这样得到的是删除边的最大条数)，最终判断一下所删除的边数是否大于等于2(是否能划分为3部分)，同时判断最后一个部分的值是否等于w或是等于0。

判断删除边是否小于k-1，通过上述操作，dfs + 贪心得到删除边数的最大条数，但还应该满足删除的最小条数小于等于k-1；因为删除后满足每一部分的异或值都相等，所以可以取奇数个相同的部分进行合并，求异或值还是等于自身；

例如：3  3  3 对其合  3 ^ 3 ^ 3 = 3 ；

代码

#include <iostream> #include <algorithm> #include <cstring> #include <vector> #include <queue> #include <unordered_map> using namespace std; typedef long long LL; const int N = 200010, INF =  0x3f3f3f3f; int a[N], b[N], nums; unordered_map<int,  vector<int>> mp; int dfs(int val, int p, int  w){     int t = a[val];      for(int x: mp[val]){         if (x != p) {             int k = dfs(x, val, w);             if (k == w) {                 nums ++;             }             else t = t ^ k;         }     }     return t; } int main(){     int t;     cin >> t;     while(t --){         int n, k;         scanf("%d%d", &n,  &k);         int t = 0;         for (int i = 1; i <= n; i ++){             scanf("%d", &a[i]);             t = t ^ a[i];         }         mp.clear();         nums = 0;         for (int i = 0; i < n - 1; i ++){             int u, v;             scanf("%d%d", &u,  &v);             mp[u].push_back(v);             mp[v].push_back(u);         }         if (t == 0)  printf("%s\\n","YES");         else {             int p = dfs(1, -1, t);             if (k > 2 && nums  >= 2 && (nums/3 + nums % 3) <= k && (p == t || p == 0))  printf("%s\\n","YES");             else printf("%s\\n",  "NO");         }     }     return 0; }

结语

本篇题解为codeforces网站上的Codeforces Round#746 (Div. 2) C题，解决方法是dfs + 贪心，最后将其限制条件进行判断，得到最终的答案；希望本文对读者有所帮助。

实习编辑：衡辉

稿件来源：深度学习与文旅应用实验室（DLETA）