力扣

Posted 2021-11-12 LinZeLiang

题目

剑指 Offer 03. 数组中重复的数字

思路1（哈希表）

• 依次遍历数组，将元素存入哈希表中，如果哈希表中已经存在，那么就找到重复的数

代码

class Solution {
    public int findRepeatNumber(int[] nums) {
        HashSet<Integer> set = new HashSet<>();
        for (int n : nums) {
            if (!set.add(n)) {
                return n;
            }
        }
        return -1;
    }
}

复杂度分析

• 时间复杂度：\\(O(N)\\)
• 空间复杂度：\\(O(N)\\)

思路2（原地交换）

• 由于数组是无序的，我们可以遍历数组，将数组的值放到对应的索引位置上，与它进行交换
• 当出现索引位置上的值已经有序，而当前的数字又需要放到该位置上，因此冲突，就找到了重复的值
• 例如：[2, 3, 1, 0, 2, 5, 3]：
  1. 2不等于当前索引值0，因此放到索引2上，然后将位置的1放到当前位置，此时：[1, 3, 2, 0, 2, 5, 3]
  2. 因为1还是不等于当前索引值0，所以将1与3交换，此时：[3, 1, 2, 0, 2, 5, 3]
  3. 因为3又不等于索引值0，所以将3与0进行交换，此时：[0, 1, 2, 3, 2, 5, 3]
  4. 然后0等于索引0，然后下一个1也等于索引值1、2也等于索引值2、3也等于索引值3
  5. 接下来到了第五个数字，2不等于索引值4，所以要放到索引为2的位置上，但是，此时索引2位置上已经是正确的2了，因此可以知道该数字重复了
  6. 最后找到重复的数字2了～

代码

class Solution {
    public int findRepeatNumber(int[] nums) {
        int length = nums.length;
        int index = 0;

        while (index < length) {
            // 如果索引和数组的值相等才进行后一位的调整
            if (nums[index] == index) {
                index++;
                continue;
            }

            // 能到这里说明当前的值不在对应的索引位置上，但是如果对应的索引位置上已经存在了值，就说明该数字重复了
            if (nums[nums[index]] == nums[index]) {
                return nums[index];
            }

            // 将当前位置的值放到对应的索引位置进行交换
            int afterIndex = nums[index];
            nums[index] = nums[afterIndex];
            nums[afterIndex] = afterIndex;
        }

        return -1;
    }
}

复杂度分析

• 时间复杂度：\\(O(N)\\)，只需遍历一次数组
• 空间复杂度：\\(O(1)\\)，在原数组操作，不需要额外的空间

我走得很慢，但我从不后退！

贪心——力扣455.分发饼干&&力扣376.摆动序列

贪心（思想：局部最优 --> 整体最优）

• 力扣455.分发饼干
• • 题目描述
  • 思路代码
• 力扣376.摆动序列
• • 题目描述
  • 思路代码

力扣455.分发饼干

题目描述

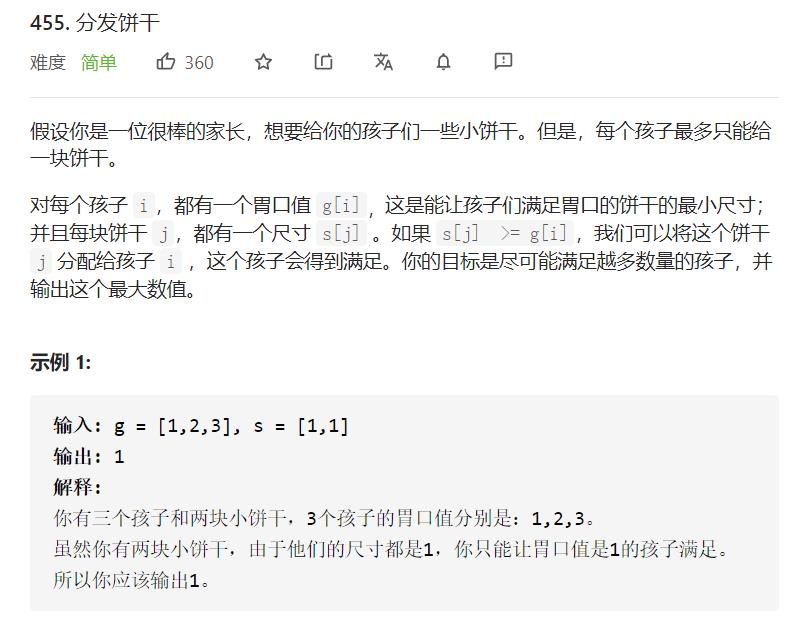
思路代码

我们应该怎么贪才是最合理，联想局部最优到整体最优，我们是不是可以先用大饼干喂大胃口，再统计小孩数量；或者先用小饼干喂小胃口，再统计小孩数量

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) 
    {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int index = 0;
        for(int i = 0; i < s.size(); i++)
        {
            if(index < g.size() && g[index] <= s[i])
            {
                index++;
            }
        }
        return index;
    }
};

力扣376.摆动序列

题目描述

思路代码

刚开始拿到题陷进去了，又想让我删或不删，还要求最大摆动序列；看了题解，才知道又是贪心，那到底怎么贪，我们先思考题目到底要求什么，求最长的摆动序列，我们再思考局部最优到整体最优，如果我们删除单调坡度上的节点，但是不删两端，那坡上是不是只剩一个波峰和波谷，那么我们只要判断局部到整体的峰值，是不是就可以算出最长的摆动序列，所以不用删除操作，我们贪的就是让峰值一直保持，然后删除单调坡度上的节点，这里用一下题解的图

prediff是前一组峰值差，curdiff是当前的峰值差，我们先默认最右端一定存在一个峰值res，初始化为1，我们需要判断满足res++的条件， prediff <= 0 && curdiff > 0 或者 prediff >= 0 || curdiff < 0，到这里问题基本就迎刃而解了

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) 
    {
        if(nums.size() <= 1) return nums.size();
        //默认最右端的峰值存在
        int res = 1;
        //前一对峰值
        int PreDiff = 0;
        //当前一对峰值
        int CurDiff = 0;

        for(int i = 0; i < nums.size() - 1; i++)
        {
            CurDiff = nums[i + 1] - nums[i];
            if((PreDiff <= 0 && CurDiff > 0) || (PreDiff >= 0 && CurDiff < 0))
            {
                res++;
                PreDiff = CurDiff;
            }
        }
        return res;
    }
};

---