字典树入门（trie）（概念+例题）

Posted 2021-11-06 xwl呀。

字典树（trie）

何为字典树

顾名思义，字典树就是一个类似于字典的东东，主要用于存储字符串以实现快速查询。

字典树长啥样？

字典树的每一个节点一共有26个子节点（一般情况），父节点与子节点所连边上都对应着一个英文字母，当我们查询一个字符串时，从根节点开始，第一个字母长啥样，我们就顺着那条对应着那个字母的边，遍历哪一个子节点，以此类推，直到遍历完成。

字典树的构建

题目往往会提供一些字符串，作为模式串，然后给出一些文本串进行操作。模式串是已知的，我们用模式串来构建字典树。对于一个模式串，比如是 \\(abcabc\\) ，我们从根节点开始，查询有没有一个子节点与根节点的连边是对应着 \\(a\\) 字符的，有，那么顺着那条边往下走，转移到一个新的节点；如果没有，那就创造出一个新的节点，让这个新节点与父节点的连边为 \\(a\\) ，以此类推下面的字符，最终到字符串末尾时，打上一个单词标记 \\(exist\\) ,来表明这个节点是一个单词的末尾。由此，存完所有字符串时，字典树也就构建完毕了。
code：

struct Trie{
	int nex[Maxn][26],cnt;
	int exist[Maxn];
	void insert(char *s,int len){
		int pos=0;
		for(int i=len-1;i>=0;i--){
			int c=s[i]-\'a\';
			if(!nex[pos][c]) nex[pos][c]=++cnt;
			pos=nex[pos][c];
		}
		exist[pos]=1;
	}
}trie;

以上是一个结构体封装的 \\(Trie\\) 。
注：\\(pos\\) 表示遍历到的节点。

查询一个单词是否出现

题目这时候或许会提供一个文本串，来问你这个串是否曾经出现过。我们就用上面提到的遍历方法，逐个遍历每一个字符，如果说查询到字典树里面没有这个节点，或者是这个节点上的标记不是 \\(true\\) ,那就返回 \\(false\\) ，表示没有这个单词，反之为 \\(true\\) 。
code:

int search(char s[],int len) {
	int pos=0;
	for(int i=0; i<len; i++) {
		int c=s[i]-\'a\';
		if(!nex[pos][c]) return false;
		pos=nex[pos][c];
	}
	return exist[pos];
}

关于全部的代码（结构体封装）

struct Trie {
	int nex[Maxn][26],cnt;
	int exist[Maxn];
	void inserct(char *s,int len) {
		int pos=0;
		for(int i=0;i<len;i++) {
			int c=s[i]-\'a\';
			if(!nex[pos][c]) nex[pos][c]=++cnt;
			pos=nex[pos][c];
		}
		exist[pos]=1;
	}
	int search(char s[],int len){
		int pos=0;
		for(int i=0;i<len;i++){
			int c=s[i]-\'a\';
			if(!nex[pos][c]) return false;
			pos=nex[pos][c];
		}
		return exist[pos];
	}
}trie;

例题：《Luogu2580：于是他错误的点名开始了》

字符串算法字典树Trie入门

基本概念

顾名思义，字典树（也叫前缀树）就是可以像字典那样来保存一些单词的集合。

如图所示：

 

 

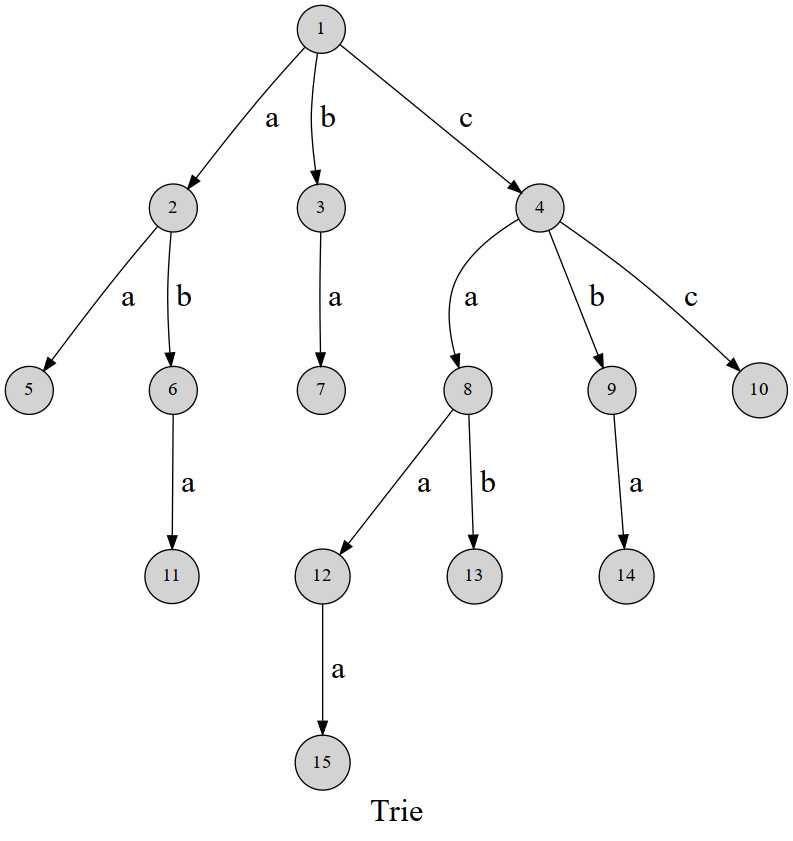
 （图片来自OIWiKi）

设根节点的标号为$0$，然后其余结点依次编号；我们用数组来存每个节点的所有子节点

更具体地，设数组$ch[MaxNode][SigmaSize]$，其中$MaxNode$表示最大可能的节点个数，$SigmaSize$是字符集合。$ch[i][j]$表示结点标号为$i$的结点 的 字母编号为$j$（比如说,j=字母-‘a‘）的子节点的结点标号。如果$ch[i][j]$为$0$，则表示$i$没有字母编号为$j$的子节点。

操作-插入

插入的时候，直接从根节点开始遍历，根据要插入的字符串往下面走，如果碰到没有的字符就新插入结点就可以了。

scanf("%s",s+1);
//插入字符串 这颗trie根节点是从1开始的 
int u=1,len=strlen(s+1);
for(int j=1;j<=len;j++)
{
    int c=s[j]-‘a‘;
    if(!ch[u][c])//原本没有这个字符
        ch[u][c]=++tot;//插入这个字符
    u=ch[u][c]; 
}

操作-查询

查询与操作是相似的，这里不再赘述。

不过要注意，在字典树里面可以查找到的不一定就是单词，还有可能是单词的前缀。

比如说字典树里面有一个单词为$apple$，查询$app$时在字典树里面会查到它，但是它只是一个前缀，不是单词。

所以我们还需要再添加一个标记数组$tag[i]$表示节点标号为$i$的结点是否为一个单词的结尾，我们把这个节点叫做单词结点。显而易见，我们之前的那个插入就要改一下了。

同样的，这个标记数组还可以干一些别的事情，比如在字符串被附了权值的情况下存这个字符串（以当前结点结尾的字符串）的权值。

scanf("%s",s+1);
int u=1,len=strlen(s+1);
for(int j=1;j<=len;j++)
{
    int c=s[j]-‘a‘;
    u=ch[u][c];
    if(!u) break;//不存在 
}
if(tag[u]==0) ...  //不存在 

 

操作-删除

其实直接把单词结点的标记清掉就可以了。

但是呢，也可以针对特殊情况特殊处理一下。

分类讨论一下：

2. 那么直接把整个单词全部删掉就可以了。(清$ch[][]$
3. 如果被删除单词的那条链上某处有了分支，然后那个分支应该是有一支是表示被删除单词的，其他的都不是，那么删掉这一支就可以了（清$ch$

其实还是有些麻烦，还不如直接清标记...

 

例题 & 模板

于是他错误的点名开始了

 1 #include<cstdio>
 2 #include<algorithm>
 3 #include<cstring>
 4 #include<vector>
 5 #include<queue>
 6 using namespace std;
 7 #define N 500005
 8 int ch[N][26];//结点i的为j+‘a‘子节点的节点标号
 9 char s[55];
10 int n,m,tag[N],tot=1; 
11 int main()
12 {
13     scanf("%d",&n);
14     for(int i=1;i<=n;i++)
15     {
16         scanf("%s",s+1);
17         //插入字符串 这颗trie根节点是从1开始的 
18         int u=1,len=strlen(s+1);
19         for(int j=1;j<=len;j++)
20         {
21             int c=s[j]-‘a‘;
22             if(!ch[u][c])//原本没有这个字符
23                 ch[u][c]=++tot;//插入这个字符
24             u=ch[u][c]; 
25         }
26         tag[u]=1;//标记这个结点是单词结点 
27         //--- 
28     }
29     scanf("%d",&m);
30     while(m--)
31     {
32         scanf("%s",s+1);
33         int u=1,len=strlen(s+1);
34         for(int j=1;j<=len;j++)
35         {
36             int c=s[j]-‘a‘;
37             u=ch[u][c];
38             if(!u) break;//名字不存在 
39         }
40         if(tag[u]==1)
41         {
42             puts("OK");
43             tag[u]=2;
44         }
45         else if(tag[u]==2)
46             puts("REPEAT");
47         else puts("WRONG");
48     }
49     return 0;
50 }

View Code

 

后记

做了例题之后，发现$Trie$干的事情$map$也能干，$Hash$也能干，不就是存个单词，查个单词嘛！

别急，他还有很多用法...检索字符串只是最基本的操作而已...