数据结构二叉树普通树与森林的定义与应用
Posted SimbaWang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构二叉树普通树与森林的定义与应用相关的知识,希望对你有一定的参考价值。
-
普通\\(m\\)叉树的性质(普通二叉树也满足)
-
各层的最大结点个数
\\[第i层最多有m^{i-1}个结点,其中1\\le i\\le h \\]-
高度为h的\\(m\\)叉树最多结点个数
\\[等比数列求和公式:\\frac{m^h-1}{m-1} \\]-
具有\\(n\\)个结点的\\(m\\)叉树至少有多高
也就是说完全m叉树的高度是多少?有以下两种表示方式:
- 高为\\(h\\)的完全二叉树最多有\\(\\frac{m^h-1}{m-1}\\)个结点,所以\\(h=⌈\\small{\\log_m[n(m-1)+1]}\\normalsize⌉\\);
- 高为\\(h\\)的完全二叉树至少有\\(\\frac{m^{h-1}-1}{m-1}+1\\)个结点,所以\\(h=⌈\\small{\\log_m[(n-1)(m-1)+1]}\\normalsize⌉+1\\);
-
\\(n\\)个结点对应\\(n-1\\)度,也就有\\(n-1\\)条边;
-
-
二叉树的常考性质(\\(n\\)为总结点数,\\(n_i\\)为度为\\(i\\)的结点数)
-
二叉树总结点数与各类型结点数的关系
\\[\\begin{cases} n=n_0+n_1+n_2 \\\\ n=0\\times n_0+1\\times n_1+2\\times n_2+1 \\end{cases} \\Longrightarrow n_0=n_2+1 \\]-
高度为\\(h\\)的霍夫曼树有\\(2h-1\\)个结点
高度为\\(h\\)的二叉树上只有度为0和度为2的结点,则此类二叉树中所包含的结点数至少为\\(2h-1\\)。
-
计算二叉树各种类型的节点的个数
-
双分支结点
\\[f(T)= \\begin{cases} 0,&如果T是空树; \\\\ f(T\\rightarrow lchild)+f(T\\rightarrow rchild),&如果T不是双分支结点; \\\\ f(T\\rightarrow lchild)+f(T\\rightarrow rchild)+1,&如果T是双分支结点; \\end{cases} \\]int TwoBranchNodes(BiTree T){ if(T == nullptr){ return 0; } else if(T->lchild != nullptr && T->rchild != nullptr){ return TwoBranchNodes(T->lchild) + TwoBranchNodes(T->rchild) + 1; } else{ return TwoBranchNodes(T->lchild) + TwoBranchNodes(T->rchild); } }-
单分支结点
\\[f(T)= \\begin{cases} 0,&如果T是空树; \\\\ f(T\\rightarrow lchild)+f(T\\rightarrow rchild),&如果T是双或者叶子; \\\\ f(T\\rightarrow lchild)+f(T\\rightarrow rchild)+1,&如果T是单分支结点; \\end{cases} \\]int OneBranchNodes(BiTree T){ if(T == nullptr){ return 0; } else if((T->lchild == nullptr) ^ (T->rchild == nullptr)){ return OneBranchNodes(T->lchild) + OneBranchNodes(T->rchild) + 1; } else{ return OneBranchNodes(T->lchild) + OneBranchNodes(T->rchild); } }-
叶子结点
\\[f(T)= \\begin{cases} 0,&如果T是空树; \\\\ f(T\\rightarrow lchild)+f(T\\rightarrow rchild),&如果T是分支结点; \\\\ 1,&如果T是叶子结点; \\end{cases} \\]int NoneBranchNodes(BiTree T){ if(T == nullptr){ return 0; } else if(T->lchild == nullptr && T->rchild == nullptr){ return 1; } else{ return NoneBranchNodes(T->lchild) + NoneBranchNodes(T->rchild); } } -
-
完全二叉树常考性质
-
完全二叉树中各类型结点的个数
\\[完全二叉树中根据n可以推出n_i的个数 \\begin{cases} 若n=2k&\\Longrightarrow n_1=1,n_0=k,n_2=k-1; \\\\ 若n=2k-1&\\Longrightarrow n_1=0,n_0=k,n_2=k-1; \\end{cases} \\]-
完全\\(m\\)叉树编号的性质
-
编号\\(i\\)的首个孩子结点(若存在)的编号
\\[(i-1)m+1+1 \\]- \\((i-1)m\\)表示前\\(i-1\\)个结点一共产生的结点数;
- 第一个1指的是根结点;
- 第二个1表示这是首个孩子;
-
编号为\\(i\\)的结点的第\\(k\\)个孩子结点(若存在)的编号
\\[(i-1)m+1+k,其中1指的是根结点,k表示这是第k个孩子 \\]-
编号为\\(i\\)的结点的双亲结点(若存在)的编号
\\[\\small{⌊\\frac{i-2}{m}⌋+1,问题b和c的逆问题。由于k不确定具体指,但k-1\\lt m,所以统一减2后向下取整} \\]-
编号为\\(i\\)的结点有右兄弟的条件,以及该右兄弟结点的编号
结点\\(i\\)不是其双亲的第\\(m\\)个子女时才有右兄弟。有以下两种阐述方式:
- 对于结点\\(j\\),其第\\(k\\)个子女结点的编号\\(i\\)为\\((j-1)m+1+k\\),只有当\\(k=m\\)时\\((i-1)\\%{m}=0\\)才会成立,若想要使得\\(i\\)不是第\\(m\\)个孩子,只需要满足$(i-1)%m!=0 $ 即可;
- 由于第\\(m\\)个孩子结点的编号为\\(jm+1\\),所以满足\\(i\\le jm=(⌊\\frac{i-2}{m}⌋+1)\\cdot m\\)也行;
-
总数为\\(n\\)个结点的\\(m\\)叉树中叶子结点的个数
由于最后一个分支结点是最后一个结点的父节点,所以其编号为\\(⌊\\frac{n-2}{m}⌋+1\\),所以叶子结点的总数为\\(n-⌊\\frac{n-2}{m}⌋+1\\)。特别地,当\\(m=2\\)时可被化简为:\\(⌊\\frac{n}{2}⌋\\)。
-
已知两结点的编号求最近的公共祖先
循环不变量:编号大的向上走。循环退出条件:编号相等。
ElemType NearestAncestor(SeqTree T, int i, int j){ if(T[i]!=\'#\' && T[j]!=\'#\'){ while(i!=j){ if(i>j){ i = i / 2; } else{ j = j / 2; } } return T[i]; } else{ cout << "传入的结点不存在!" << endl; exit(0); } }-
完全二叉树的高度
具有\\(n\\)个(\\(n\\gt0\\))结点的完全二叉树的高度\\(h=⌈\\log_2(n+1)⌉\\)或者\\(⌊\\log_2(n)+1⌋\\);
-
完全二叉树的判定
空结点后不能出现非空结点(层次遍历纳入空结点)
bool IsComplete(BiTree T){ InitQueue(Q); if(!T){ return true; } else{ EnQueue(Q, T); while(!IsEmpty(Q)){ DeQueue(Q, parentNode); if(parentNode != nullptr){ EnQueue(Q, parentNode->lchild); EnQueue(Q, parentNode->rchild); } else{ // 空结点之后必须全为空结点才能返回TRUE while(!IsEmpty(Q)){ DeQueue(Q, parentNode); if(parentNode != nullptr){ // 如果不是空节点,则说明叶子结点后面还存在非叶子结点,这个非叶子节点的孩子节点就是此非空节点 return false; } }// End While }// End parentNode==nullptr }// End While return true; }// End T!=nullptr }-
满二叉树确定二叉链表的结构
可以仅通过先序或者后序或者层序(不需要中序)!因为对于一棵满二叉树而言,每一个双分支结点都有相等长度的左右子树,故而不需要中序序列确定左右子树的长度。
-
先序遍历序列唯一确定
BiTree PreOrder(char order[], int preLow, int preHigh) { if (preHigh >= preLow) { // 左右子树的长度为half int half = (preHigh - preLow) / 2; BiTree root = (BiTree)malloc(sizeof(BiTreeNode)); // 创建根结点 root->data = order[preLow]; // 创建左子树 root->lchild = PreOrder(order, preLow+1, preLow+half); // 创建左子树 root->rchild = PreOrder(order, preLow+half+1, preHigh); return root; } else { return nullptr; } }-
后序遍历序列唯一确定
BiTree PostOrder(char order[], int preLow, int preHigh) { if (preHigh >= preLow) { // 左右子树的长度为half int half = (preHigh - preLow) / 2; BiTree root = (BiTree)malloc(sizeof(BiTreeNode)); // 创建左子树 root->lchild = PostOrder(order, preLow, preLow+half-1); // 创建左子树 root->rchild = PostOrder(order, preLow+half, preHigh-1); // 创建根结点 root->data = order[preHigh]; return root; } else { return nullptr; } }-
层序遍历序列唯一确定
这个可以用满二叉树编号的性质。
BiTree LevelOrder(char order[], int levelRoot){ if(levelRoot <= N){ BiNode* root = (BiNode*)malloc(sizeof(BiNode)); // 创建根结点 root->data = order[levelRoot]; // 创建左子树 root->lchild = LevelOrder(order, 2*levelRoot); // 创建右子树 root->rchild = LevelOrder(order, 2*levelRoot+1); } else{ return nullptr; } }-
其中先序和后序的转化是最简单的
只要递归地将根结点与子树的节点换位即可。如下图所示:
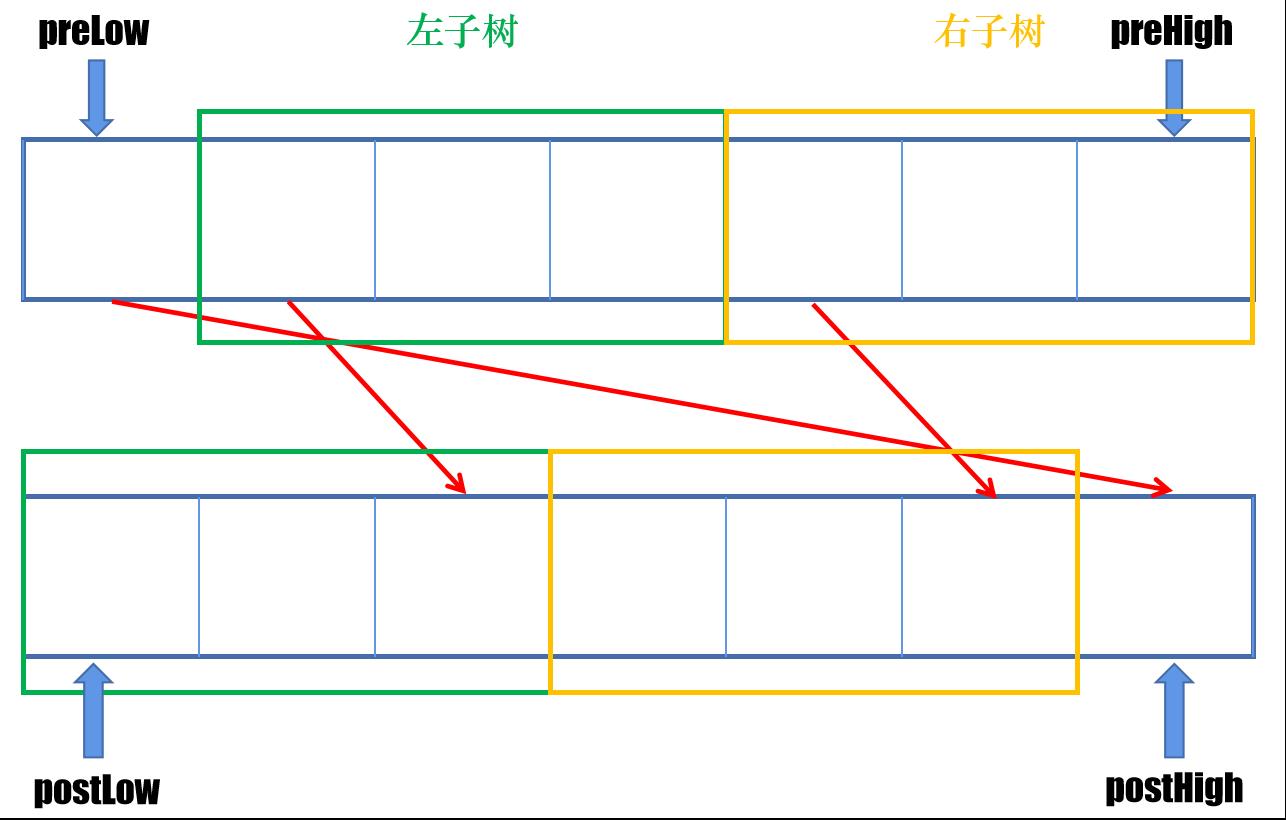
void PreToPost(BiTree pre[], int preLow, int preHigh, BiTree post[], int postLow, int postHigh) { int half; if (preHigh >= preLow) { // 转换根结点(根结点后置) post[postHigh] = pre[preLow]; half = (preHigh - preLow) / 2; // 转换左子树(左子树前移) PreToPost(pre, preLow + 1, preLow + half, post, postLow, postLow + half - 1); // 转换右子树(右子树前移) PreToPost(pre, preLow + half + 1, preHigh, post, postLow + half, postHigh - 1); } }
-
-
二叉树遍历的应用
-
求二叉树树高
-
递归算法(后序遍历)
// 树高 = 左右子树的最大值 + 1(根节点) int BiTreeDepth(BiTree TRoot){ if(TRoot == nullptr){ return 0; } else{ int leftDepth = BiTreeDepth(TRoot->lchild); int rightDepth = BiTreeDepth(TRoot->rchild); return Max(leftDepth, rightDepth) + 1; } }时间复杂度:\\(O(n)\\),空间复杂度:\\(O(\\mathbf{Height}(T))\\)【平衡时才是:\\(O(⌈\\log_2(n+1)⌉)\\)】;
-
非递归算法(层序遍历+辅助队列)
int GetBiTreeWidth(BiTree T){ if(!T){ return 0; } else if(T->lchild == nullptr && T->rchild == nullptr){ return 1; } else{ // 创建一个辅助队列并初始化 AuxQue auxque; InitQueue(auxque); auxque->front = auxque->rear = -1; // 记录父层的层号、最右端结点的序号,子层的结点个数(已访问) // 父层:上一层(删除结点层);子层:当前层(插入结点层) int depth, lastNodeOrder, nodeCount; // 将根节点插入队列中(插入后根节点所在的层变成父层) auxque->data[++auxque->rear] = T; depth = 0, lastNodeOrder = auxque->rear, nodeCount = 0; while(auxque->front < auxque->rear){ // 将父层的元素取出,移动front指针 TreeNode parentNode = auxque->data[++auxque->front]; // 插入孩子结点,并使结点计数器自增1 if(parentNode->lchild != nullptr){ auxque->data[++auxque->rear] = parentNode->lchild; nodeCount++; } if(parentNode->rchild != nullptr){ auxque->data[++auxque->rear] = parentNode->rchild; nodeCount++; } // front指针指向了父层的最右端元素,父层的最后一个元素被弹出 if(auxque->front == lastNodeOrder){ // 同时子层的最后一个节点也插入完成了,子层变成了新的父层 lastNodeOrder = auxque->rear; depth++; nodeCount = 0; } }// End While return depth; } }时间复杂度:\\(O(n)\\),空间复杂度:\\(O(n)\\);
-
求二叉树树宽
-
递归算法(先序遍历+辅助数组)
#define MAX_HEIGHT 100 void PreOrder(BiTree T, int level, int* width){ if(!T){ return; } else{ width[level]++; PreOrder(T->lchild, level + 1, width); PreOrder(T->rchild, level + 1, width); } } int GetBiTreeWidth(BiTree T){ int* width = (int*)malloc(sizeof(int) * MAX_HEIGHT); for(int i=0; i<MAX_HEIGHT; i++){ width[i] = 0; } PreOrder(T, 1, width); int maxWidth = 0; for(int i=0; i<MAX_HEIGHT; i++){ maxWidth = maxWidth < width[i] ? width[i] : maxWidth; } return maxWidth; }时间复杂度:\\(O(n)\\),空间复杂度:\\(O(\\mathbf{Height}(T))\\);【平衡时才是:\\(O(⌈\\log_2(n+1)⌉)\\)】
-
非递归算法(层序遍历+辅助队列)
int GetBiTreeWidth(BiTree T){ if(!T){ return 0; } else if(T->lchild == nullptr && T->rchild == nullptr){ return 1; } else{ // 创建一个辅助队列并初始化 AuxQue auxque; InitQueue(auxque); auxque->front = auxque->rear = -1; // 记录父层的宽度、最右端结点的序号,子层的结点个数(已访问) // 父层:上一层(删除结点层);子层:当前层(插入结点层) int width, lastNodeOrder, nodeCount; // 将根节点插入队列中(插入后根节点所在的层变成父层) auxque->data[++auxque->rear] = T; width = 1, lastNodeOrder = auxque->rear, nodeCount = 0; while(auxque->front < auxque->rear){ // 将父层的元素取出,移动front指针 TreeNode parentNode = auxque->data[++auxque->front]; // 插入孩子结点,并使结点计数器自增1 if(parentNode->lchild != nullptr){ auxque->data[++auxque->rear] = parentNode->lchild; nodeCount++; } if(parentNode->rchild != nullptr){ auxque->data[++auxque->rear] = parentNode->rchild; nodeCount++; } // front指针指向了父层的最右端元素,父层的最后一个元素被弹出 if(auxque->front == lastNodeOrder){ // 同时子层的最后一个节点也插入完成了,子层变成了新的父层 lastNodeOrder = auxque->rear; width = Max(width, nodeCount); nodeCount = 0; } }// End While return width; } }时间复杂度:\\(O(n)\\),空间复杂度:\\(O(n)\\);
-
遍历序列确定二叉链表(思想是重点)
-
先中序列
先序遍历序列确定根结点,中序遍历中确定左右子树及各子树的长度,回到先序遍历序列通过子树长度确定子树所在的范围,然后再确定左右子树的根结点。
BiTree CreateBiTree(ElemType* PreOrder, ElemType* InOrder, int PreLow, int PreHigh, int InLow, int InHigh){ int parentIndexPre, parentIndexIn; // 在InOrder序列中从InLow到InHigh查找根结点PreOrder[parentIndexPre] parentIndexPre = PreLow, parentIndexIn = FindIndex(InOrder, PreOrder[parentIndexPre], InLow, InHigh); // 创建根结点 BiNode* parentNode = (BiNode*)malloc(sizeof(BiNode)); parentNode->data = InOrder[parentIndexIn]; // 通过中序遍历中根结点的编号确定左右子树的长度 int lchildLength = parentIndexIn - InLow; int rchildLength = InHigh - parentIndexIn; // 创建左子树 if(lchildLength != 0) { parentNode->lchild = CreateBiTree(PreOrder, InOrder, PreLow+1, PreLow+lchildLength, InLow, InLow+lchildLength-1); } else { parentNode->lchild = nullptr; } // 创建右子树 if(rchildLength != 0) { parentNode->rchild = CreateBiTree(PreOrder, InOrder, PreHigh-rchildLength+1, PreHigh, InHigh-rchildLength+1, InHigh); } else { parentNode->rchild = nullptr; } return parentNode; }-
后中序列
后序遍历序列确定根结点,中序遍历中确定左右子树及各子树的长度,回到后序遍历序列通过子树长度确定子树所在的范围,然后再确定左右子树的根结点。
BiTree CreateBiTree(ElemType* PostOrder, ElemType* InOrder, int PostLow, int PostHigh, int InLow, int InHigh){ int parentIndexPost, parentIndexIn; // 在InOrder序列中从InLow到InHigh查找根结点PostOrder[parentIndexPost] parentIndexPost = PostHigh, parentIndexIn = FindIndex(InOrder, PostOrder[parentIndexPost], InLow, InHigh); // 创建根结点 BiNode* parentNode = (BiNode*)malloc(sizeof(BiNode)); parentNode->data = InOrder[parentIndexIn]; // 通过中序遍历中根结点的编号确定左右子树的长度 int lchildLength = parentIndexIn - InLow; int rchildLength = InHigh - parentIndexIn; // 创建左子树 if(lchildLength != 0) { parentNode->lchild = CreateBiTree(PostOrder, InOrder, PostLow, PostLow+lchildLength-1, InLow, InLow+lchildLength-1); } else { parentNode->lchild = nullptr; } // 创建右子树 if(rchildLength != 0) { parentNode->rchild = CreateBiTree(PostOrder, InOrder, PostHigh-rchildLength, PostHigh-1, InHigh-rchildLength+1, InHigh); } else { parentNode->rchild = nullptr; } return parentNode; }-
层中序列
层序遍历的规则是:遍历孩子结点之前先把孩子结点的所有祖先结点和其左(堂)兄弟遍历一遍。所以当我们拿到层序遍历序列中的某个结点时,我们可以肯定的说:“我们有能力将其所有祖先结点构造好!”,故而只需要在中序序列中确定它与根结点的相对位置就行了。
#include<map> #define MAX_SIZE 100 // 定义层序序列和先序序列 ElemType levelOrder[MAX_SIZE], inOrder[MAX_SIZE]; // 定义记录中序序列各个结点位置的字典(映射):{结点值:结点在中序序列中的编号} map<ElemType, int> inPos;// 在指定levelIndex位置创建root结点 void CreateBiTreeNode(BiTreeNode*& root, int levelIndex){ // 如果走到了现有的树的底部,则新创建结点(构造祖先结点) if(root == nullptr){ root = (BiTreeNode*)malloc(sizeof(BiTreeNode)); root->data = levelOrder[levelIndex]; root->lchild = root->rchild = nullptr; return; } // 如果层序中的结点在中序序列中的位置靠左, // 表明该结点在其根结点的左边,让根结点移向其左孩子 else if(inPos[root->data] >= inPos[levelOrder[levelIndex]]){ CreateBiTreeNode(root->lchild, levelIndex); } // 否则表明在根结点的右边,让根结点移向其右孩子 else{ CreateBiTreeNode(root->rchild, levelIndex); } }// 创建二叉树 void CreateBiTree(BiTree& BT){ for(int i=0; i<n; i++){ CreateBiTreeNode(BT, i); } }-
总结(给啥序列就按照啥规则办事)
- 给先序序列:(前序规则)从先序数组起始处确定根结点,再在中序中查找根结点的位置,然后确定根结点的左右子树;
- 给后序序列:(后序规则)从后序数组末尾处确定根结点,再在中序中查找根结点的位置,然后确定根结点的左右子树;
- 给层序序列:(层序规则)从头到尾遍历层序数组,再在中序序列中确定该结点与根结点的关系,并一层一层下坠;
-
先序、中序和后序线索二叉树的构造
#define THREAD 1 #define LINK 0 // 将二叉链表线索化的函数 void Threading(BiTreeNode current, BiTreeNode& previous){ // 左子树为空,则建立前驱线索 if(current != nullptr && current->lchild == nullptr){ // 判断cur!=nullptr是因为美观,cur一直不会为空,因为递归遍历有if保证 current->lchild = previous; current->ltag = THREAD; } // 右子树为空,则建立后继线索 if(previous != nullptr && previous->rchild == nullptr){ // 判断pre!=nullptr是因为pre初始化为nullptr previous->rchild = current; prevoius->rtag = THREAD; } // 向前移动 previous = current; }-
递归算法(树的递归特性)
// 定义函数指针类型指明传入的是哪一种遍历方式 typedef void (*OrderThreading)(BiTree current,BiTree& previous); // 创建线索化二叉链表 void CreateThreadTree(BiTree T, OrderThreading OT){ BiTreeNode previous = nullptr; if(T != nullptr){ OT(T->lchild, prevoius); // 为最后一个结点做后继线索化 if(previous->rchild == nullptr){ previous->rtag = THREAD; } } }// 先序遍历 void PreOrderThreading(BiTree current,BiTree& previous){ if(current != nullptr){ Threading(current, previous); // 防止先序遍历时产生“爱滴魔力转圈圈”的情况 if(current->ltag == LINK){ PreOrderThreading(current->lchild, previous); } PreOrderThreading(current->lchild, previous); } } // 中序遍历 void InOrderThreading(BiTree current,BiTree& previous){ if(current != nullptr){ PreOrderThreading(current->lchild, previous); Threading(current, previous); PreOrderThreading(current->lchild, previous); } } // 后序遍历 void PostOrderThreading(BiTree current,BiTree& previous){ if(current != nullptr){ PreOrderThreading(current->lchild, previous); PreOrderThreading(current->lchild, previous); Threading(current, previous); } }【注】出现“爱滴魔力转圈圈”问题是因为:在访问后继结点之前[1],后继结点的前驱线索指针与后继指针重合[2]。[1]指明根结点需要先访问,所以只会发生在先序遍历中;[2]只能是左孩子指针才能“身兼二职”。
-
非递归算法(用辅助栈实现非递归的遍历)
先序遍历和中序遍历很相似,一个是在压入栈之前访问
(入栈序列),一个是弹出栈之后访问(出栈序列)。由于头插法的性质,辅助栈栈顶元素即是前驱结点。// 先序遍历 void PreOrderThreading(BiTree T){ InitStack(S); BiTreeNode current = T; // 当前指针不空或者辅助栈不空就继续 while(current != nullptr || !IsEmpty(S)){ // 防止出现“爱滴魔力转圈圈”的情况 if(current != nullptr && current->ltag == LINK){ BiTreeNode previous = nullptr; GetTop(S, previous); Threading(current, previous); // 将线索化后的根结点压入栈中,并继续向左移动 Push(S, current); current = current->lchild; } else{ // 将根结点取出并向右移动 Pop(S, current); current = current->rchild; } } } // 中序遍历 void InOrderThreading(BiTree T){ InitStack(S); BiTreeNode current = T; // 当前指针不空或者辅助栈不空就继续 while(current != nullptr || !IsEmpty(S)){ if(current != nullptr){ // 将根结点压入栈中,并继续向左移动 Push(S, current); current = current->lchild; } else{ // 将根结点取出,线索化后再向右移动 Pop(S, current); BiTreeNode previous = nullptr; GetTop(S, previous); Threading(current, previous); current = current->rchild; } } }后序遍历就完全不同了,因为必须保证左右子树都要访问完成,所以必须借助“前驱指针\\(\\mathbf{previous}\\)证明是否被访问过”进行流程控制,这就大大增加了难度。
// 后序遍历 void PostOrderThreading(BiTree T){ // 倘若不想使用栈,则需要使用三叉链表的存储结构(第三叉指向双亲节点) InitStack(StackOfParent); BiNode* cursor, previous; cursor = T, previous = nullptr; while(cursor || !IsEmpty(StackOfParent)){ // 因为我们需要将cursor压入栈内,所以不能仅仅判断cursor有无左孩子 if(cursor){ // 如果当前位置存在节点,则将其作为“双亲节点”入栈 Push(StackOfParent, cursor); // 并指向自己的左孩子(继续向左走) cursor = cursor->lchild; } else{ // 如果当前位置不存在节点,说明向左走走到头了,需要向右转后者向上走(如果没有右孩子或者已经向右转过则不需要了) GetTop(StackOfParent, parent); // 如果右兄弟存在且没有被访问过,则向右转 if(parent->rchild!=nullptr && parent->rchild!=previous){ // 不判断右兄弟是否存在会造成死循环 cursor = parent->rchild; } // 向上走 else{ // 说明该双亲结点的左右子树都已经访问完成了(或者没有孩子),所以弹出双亲节点 Pop(StackOfParent, parent); // 访问“根”(也就是双亲结点) BiTreeNode previous = nullptr; GetTop(StackOfParent, previous); Threading(parent, previous); // 移动前驱指针 previous = parent; // 为了后续操作为向右转向(因为根节点访问完了就代表这一整棵子树已经访问完成,所以需要向上向右走转向右兄弟树) cursor = nullptr; } } } }-
先中后序遍历查找的前驱后继(手算的方法)
-
先序遍历查找前驱后继(需要三叉链表获取双亲结点)
-
若
p->rtag == THREAD,即结点已被后继线索化,则next = p->rchild; -
若
p->ltag == THREAD,即结点已被前驱线索化,则previous = p->lchild; -
若
p->rtag == LINK,即结点未被后继线索化(分支结点),则该节点必有右孩子,按照“根[左]右”的规则可以分2种情况:
- 有左孩子,即
p->lchild != nullptr:next = p->lchild; - 无左孩子,即
p->lchild == nullptr:next = p->rchild;
- 若
p->ltag == LINK,即结点未被前驱线索化(分支结点),但是先序遍历的前驱是比不会存在于其左右子树中的,所以需要借助三叉链表获取其双亲结点。
-
p是左孩子:则由“根(p左右)[右]”可知,
previous = p->parent; -
p是右孩子,且没有左兄弟:则由“根(p左右)”可知,
previous = p->parent; -
p是右孩子,存在左兄弟:则由“根(根左右)(p左右)”可知,
previous = 左兄弟的右优先叶子结点;

-
中序遍历查找前驱后继
- 若
p->rtag == THREAD,即结点已被后继线索化,则next = p->rchild; - 若
p->ltag == THREAD,即结点已被前驱线索化,则previous = p->lchild; - 若
p->rtag == LINK,即结点未被后继线索化(分支结点),则该节点必有右孩子,所以next = 右子树最左下结点; - 若
p->ltag == LINK,即结点未被前驱线索化(分支结点),则该节点必有左孩子,所以previous = 左子树最右下结点;(出现右子树向左走,否则向左)
-
后序遍历查找前驱后继(需要三叉链表获取双亲结点)
-
若
p->rtag == THREAD,即结点已被后继线索化,则next = p->rchild; -
若
p->ltag == THREAD,即结点已被前驱线索化,则previous = p->lchild; -
若
p->ltag == LINK,即结点未被前驱线索化(分支结点),则该节点必有左孩子,按照“左[右]根”的规则可以分2种情况:
- 有右孩子,即
p->rchild != nullptr:previous = p->rchild; - 无右孩子,即
p->rchild == nullptr:previous = p->lchild;
- 若
p->rtag == LINK,即结点未被后继线索化(分支结点),但是后序遍历的后继是比不会存在于其左右子树中的,所以需要借助三叉链表获取其双亲结点。
-
p是右孩子:则由“[左](左右p)根”可知,
next = p->parent; -
p是左孩子,且没有右兄弟:则由“(左右p)根”可知,
next = p->parent; -
p是左孩子,存在右兄弟:则由“(左右p)(左右根)根”可知,
next = 右兄弟的左优先叶子结点;(出现左子树向左走,否则向右)
先序线索二叉树 中序线索二叉树 后序线索二叉树 找前驱 × √ √ 找后继 √ √ × 【注】湖南大学866数据结构是不考察线索化的,所以重点是
如何查找没有线索化的前驱后继。-
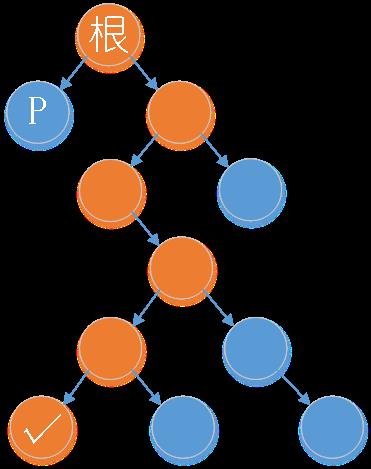
二叉树的溯源问题(如何保存遍历路径:栈+后序!)
问题:打印出值为\\(x\\)的结点的所有祖先结点(假设值为\\(x\\)的结点最多有1个)
由于要保存所有祖先结点,所以必须使用后序遍历,保证根结点最后访问!
void SearchAncestors(BiTree T, ElemType x){ // 倘若不想使用栈,则需要使用三叉链表的存储结构(第三叉指向双亲节点) InitStack(StackOfAncestor); BiTree cursor, previous; cursor = T, previous = nullptr; while(cursor || !IsEmpty(StackOfAncestor)){ // 因为我们需要将cursor压入栈内,所以不能仅仅判断cursor有无左孩子 if(cursor){ // 如果当前位置存在节点,则将其作为“双亲节点”入栈 Push(StackOfAncestor, cursor); // 并指向自己的左孩子(继续向左走) cursor = cursor->lchild; } else{ // 如果当前位置不存在节点,说明向左走走到头了,需要向右转后者向上走(如果没有右孩子或者已经向右转过则不需要了) BiTree parent = nullptr; GetTop(StackOfAncestor, previous); // 如果右兄弟存在且没有被访问过,则向右转 if(parent->rchild!=nullptr && parent->rchild!=previous){ // 不判断右兄弟是否存在会造成死循环 cursor = parent->rchild; } // 向上走 else{ // 说明该双亲结点的左右子树都已经访问完成了(或者没有孩子),所以弹出双亲节点 Pop(StackOfAncestor, parent); // 访问“根”(也就是双亲结点) if(parent->data == x){ printf("所查结点的所有祖先的值为:"); while(!IsEmpty(StackOfAncestor)){ BiTree ancestor = nullptr; Pop(StackOfAncestor, ancestor); printf(&(ancestor->data)); printf(" "); } // 直接退出函数体 exit(1); } // 将previous指针指向最近访问过的双亲结点(前驱) previous = parent; // 为了后续操作为向右转向(因为根节点访问完了就代表这一整棵子树已经访问完成,所以需要向上向右走转向右兄弟树) cursor = nullptr; } } } }王道给出的更简洁的方法,但是与之前所学的后序遍历非递归实现不同,换了一种栈的数据结构,并且换了一种遍历方式:首先遍历左子树,与此同时访问根结点(可以理解为利用先序遍历节省时间,因为如果在遍历左子树时就找到了x,我们就能直接跳出循环了);如果左子树中没有找到,就去最近的没有被访问过的右子树中搜索(由于栈中保存了\\(\\mathbf{tag}\\)作为对左右子树访问完成的标识,所以不需要用\\(\\mathbf{previous}\\)指针了)。所以这很难说是严格的后序遍历,不过要说是“打了小抄”或者“乐于剧透”的后序遍历我倒是不否认。
typedef struct{ BiTree bt; int tag; // 值为0表示左孩子已经被访问,值为1表示右孩子已经被访问 }Stack;void Search(BiTree bt, char x) { Stack s[10]; //栈容量足够大 int top = 0; while (bt != nullptrptr || top > 0) { // 首先遍历左子树,这里访问根结点:bt->data != x(打个小抄,剧透一下) if (bt != nullptrptr && bt->data != x) { // 如果恰好x出现在左子树中我们就能跳过之后的遍历了 s[++top].bt = bt; s[top].tag = 0; bt = bt->lchild; } else { // 如果在左子树中找到了x结点(并不是在访问“根结点”) if (bt && bt->data == x) { printf("所查结点的所有祖先结点的值为∶\\n"); for (i = 1; i <= top; i++) printf("%c", s[i].bt->data); exit(1); } // 继续在右子树中搜索x结点 else { // 如果右孩子被访问了则返回到:最近的、没有访问右孩子的结点处 while(top != 0 && s[top].tag == 1) top--; // 如果没有退到根结点,表示还可以继续向右执行 if(top != 0) { s[top].tag = 1; bt = s[top].bt->rchild; } } } } }-
寻找指定两个结点的最近公共祖先结点
问题:设一棵二叉树的结点结构为\\((\\mathbf{lchild},\\mathbf{info},\\mathbf{rchild})\\),\\(\\mathbf{root}\\)为指向该二叉树根结点的指针,\\(p\\)和\\(q\\)分别为指向该二叉树中任意两个结点的指针,试编写算法\\(\\mathbf{Ancestor}(\\mathbf{root},p,g,r)\\),找到\\(p\\)和\\(q\\)的最近公共祖先结点\\(r\\)。
由(g)可知此问题可以被转化为求两个栈的第一个公共元素。故核心思想为:采用后序遍历的方式在栈中保存所有“根结点”。找到\\(p\\)结点后将当前栈中所有元素复制到另一辅助栈中,然后继续寻找\\(q\\)结点。最后比较两个栈中的元素,第一个匹配(相等)的即是\\(p\\)、\\(q\\)结点的最近公共祖先结点\\(r\\)。
typedef struct{ BiTree bt; int tag; // 值为0表示左孩子已经被访问,值为1表示右孩子已经被访问 }Stack; // 栈的深拷贝 void StackCopy(Stack s1[], int tops1, Stack s2[], int& tops2){ for(int i=0; i<=tops1; i++){ s2[i] = s1[i]; } tops2 = tops1; } // 寻找两个栈的第一个公共元素 BiTree SearchFirstPublicElem(Stack s1[], int tops1, Stack s2[], int tops2){ for (int i1 = tops1; i1 > 0; i1--) { for (int i2 = tops2; i2 > 0; i2--) { if (s1[i1].bt == s2[i2].bt) { return s1[i1].bt; } } } return nullptr; } Stack s[10], auxs[10] // 定义栈和辅助栈BiTreeNode* SearchNearestPublicAncestor(BiTree root, BiTreeNode* p, BiTreeNode* q){ // 定义流程控制变量:控制栈的拷贝 bool isTwiceFind = false; // 定义两个栈的栈顶游标 int tops, topauxs; // 将根结点入栈 BiTreeNode* cursor = root; // 索引为0的位置不用(与数据结构吻合) tops = topauxs = 0, s[++tops] = cursor; // 如果没到尽头,或者栈非空,则继续循环 while(cursor != nullptr || tops > 0){ // 首先在左子树中寻找p结点和q结点,并“剧透一下” if(cursor != nullptr && cursor != p && cursor != q){ s[++tops].bt = cursor; s[tops].tag = 0; cursor = cursor->lchild; } else{ // 如果在左子树中找到了p结点或者q结点 if(cursor != nullptr){ // 第一次找到p或者q,则拷贝栈中元素 if(!isTwiceFind){ StackCopy(s,tops,auxs,topauxs); isTwiceFind = true; // 回到开始的if继续在左子树中搜索 } // 第二次找到p或者q,则寻找两个栈中的最近公共祖先结点 else{ return SearchFirstPublicElem(s,tops,auxs,topauxs); } } // 如果两个结点都没有在左子树中找到,则去右子树中搜索 else{ // 退回至最近的、没有被访问右子树的“根结点” while(tops != 0 && s[tops].tag == 1){ tops--; } // 如果没有退回到根结点,则继续向右子树中寻找 if(tops != 0){ BiTreeNode* parent = s[tops].bt; cursor = parent->rchild; } } } } }-
求先、中和后序遍历序列中的第\\(k(1\\le k\\le n)\\)个结点的值
-
先序遍历
先序遍历的思想是“根左右”,当根结点不是\\(\\mathbf{KNode}\\)时,我们在左右子树中搜索。先在左子树中搜索\\(\\mathbf{KNode}\\),如果存在则返回k,不再继续搜索右子树;否则返回其左子树最后一个被先序遍历的结点的编号,然后转向其右子树进行搜索,如果搜索到了则返回k。否则表明左右子树中也没有搜索到,则返回至双亲结点并在下一棵树中搜索\\(\\mathbf{KNode}\\)。
// cursor表示当前节点在先序遍历中的序号(初始值为0) int FindKNode_Pre1(BiTree T, int cursor, int k, BiTree& KNode){ if(T != nullptr){ // 在根结点处搜索 if(++cursor == k){ KNode = T; // 赶紧return,不再进入子树中搜索(节约时间) return cursor; } // 继续向左走并记录左子树最后一个被遍历的结点的编号 cursor = FindKNode_Pre(T->lchild, cursor, k, KNode); // 在左子树中找到了,则向上一直返回k,不再遍历其右子树; if(cursor == k){ return k; } // 左子树全部走完之后都没有找到,则向右走在右子树中搜索; else{ return FindKNode_Pre(T->rchild, cursor, k, KNode); } // 如果k>n则会将树完全遍历,不会产生无限递归 } else{ // 返回到其双亲结点 return cursor; } }// 方法二:王道的解法。思想是差不多的,只不过我是将left==k作为标记,而王道则是重新创造了一个#作为标记,这样更加简洁 int i = 1; char FindKNode_Pre2(BiTree T, int k){ if (!T) return \'#\'; if (i == k) // 如果是第k个,则返回该节点的值 return T->data; i++; char ch = FindKNode_2(T->lchild, k); // 如果不是空结点表示在左子树中找到了KNode,否则在右子树中继续搜索 return ch != \'#\' ? ch : FindKNode_2(T->rchild, k); }-
中序遍历(二叉查找树的第k个结点)
// cursor表示当前节点在中序遍历中的序号(初始值为0) int FindKNode_In1(BiTree T, int cursor, int k, BiTree& KNode) { if (T != nullptrptr) { // 先在左子树中搜索,并记录左子树在中序遍历中的最后一个结点编号 cursor = FindKNode_In(T->lchild, cursor, k, KNode); // 如果在左子树中搜索到了则向上返回k, if (cursor == k) { return k; } // 左子树中没有找到,搜索根结点和右子树 else { // 搜索根结点,如果根结点是KNode则返回 if (++cursor == k) { KNode = T; return cursor; } // 否则继续向右子树中搜索KNode else { return FindKNode_In(T->rchild, cursor, k, KNode); } } } else { return cursor; } }// 方法二:王道的Style int i = 1; char FindKNode_In2(BiTree T, int k) { if(!T) return \'#\'; // 首先搜索左子树,如果搜索到了ch!=\'#\' char ch = FindKNode_In(T->lchild, k); if(ch != \'#\') return ch; // 左子树没有搜索到则搜索根结点 if(++i == k) return T->data; // 根结点没有则继续在右子树中搜索 else return FindKNode_In(T->rchild, k); }-
后序遍历
// cursor表示当前节点在后序遍历中的序号(初始值为0) int FindKNode_Post1(BiTree T, int cursor, int k, BiTree& KNode) { if (T != nullptrptr) { // 先在左子树中搜索,并记录左子树在中序遍历中的最后一个结点编号 cursor = FindKNode_Post(T->lchild, cursor, k, KNode); // 如果在左子树中搜索到了则向上返回k,否则 if (cursor == k) { return k; } // 左子树树的存储结构;树与二叉树的转换;树和森林的遍历算法
以上是关于数据结构二叉树普通树与森林的定义与应用的主要内容,如果未能解决你的问题,请参考以下文章
-