数据结构&算法07-链表技巧&参考源码

Posted 2021-11-05 李柱明

目录

• 前言
• 指针或引用的含义
• 指针丢失和内存泄漏
• 哨兵简化实现难度
• 边界条件处理

---

前言

1. 指针或引用的含义
2. 指针丢失和内存泄漏
3. 哨兵简化实现难度
4. 边界条件处理
5. 多看代码多练

李柱明博客：https://i.cnblogs.com/posts/edit-done;postId=15487326

指针或引用的含义

指针和引用都是一个意思，都是存储所指对象的内存地址。

理解指针非常重要，对于后期使用指针、函数传参等等都发挥着理论指导作用。

指针：

• 变量的地址即为该变量的指针 ，理解为地址（指针）指向了该变量，也就是通过地址（指针）可以找到该变量。
• 如果一个变量专门用来存放另一个变量的地址（指针），则称它为指针变量。
• 如一个 32bit 系统中，指针的值只是 4 个 byte 的数据而已。

指针丢失和内存泄漏

指针丢失&内存泄漏例子：

• 如单向链表，插入节点时，注意指针的更新：

• // 错误示范
  p->next = x;  // 将 p 的 next 指针指向 x 结点；
  x->next = p->next;  // 将 x 的结点的 next 指针指向 b 结点；
  

• 上述代码中一个错误点就是：p->netx 已经由原来的 b 更新为 x 了，到第二行代码时原意为 x 的下一个想指向 b 的，但是指针丢失了，导致 x->next 指向了 x 本身，链表后面的节点全部丢失。后面丢失的节点就是内存泄漏了。

• 

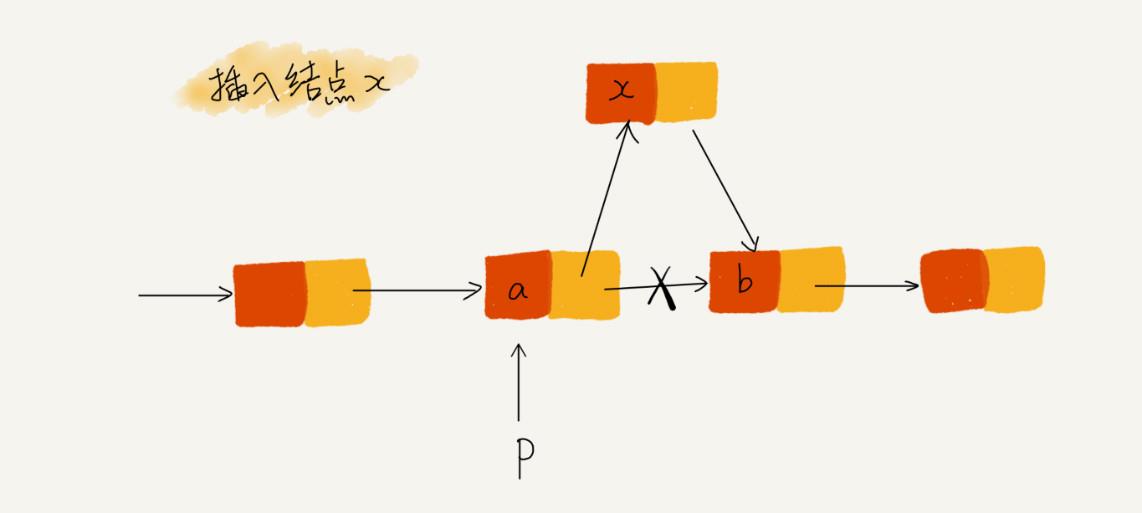
• 注意：

  • 实时留意指针的状态。
  • 在操作链表时，必要时可以备份节点。如在删除单向链表的某个节点时，备份下前一个节点。
  • 删除节点时，释放节点内存。若有对应的指针变量，记得赋空值。

注意野指针：

• 指针变量创建时记得赋空值。
• 释放内存时，记得赋空值。

哨兵简化实现难度

哨兵为了处理边界问题。如首节点。

哨兵不参与逻辑业务。

编程建议：链表尽量弄个链表句柄，方便管理。首节点的指针可以当做链表的句柄使用。

在链表中，第一个节点都需要特殊处理，如删除单向链表的第一个节点，就得把指向该链表的指针更新为第二个节点。

这样每次操作链表都需要检查是否是第一个节点，如果是还要特殊处理，显得繁琐。

所以我们固定一个首节点，实际数据的节点从第二个节点开始。这样就不用管链表是否为空。

首节点还可以记录链表的一些数据。

首节点的指针可以当做链表的句柄使用。

含首节点的链表交带头链表，相反叫不带头链表。

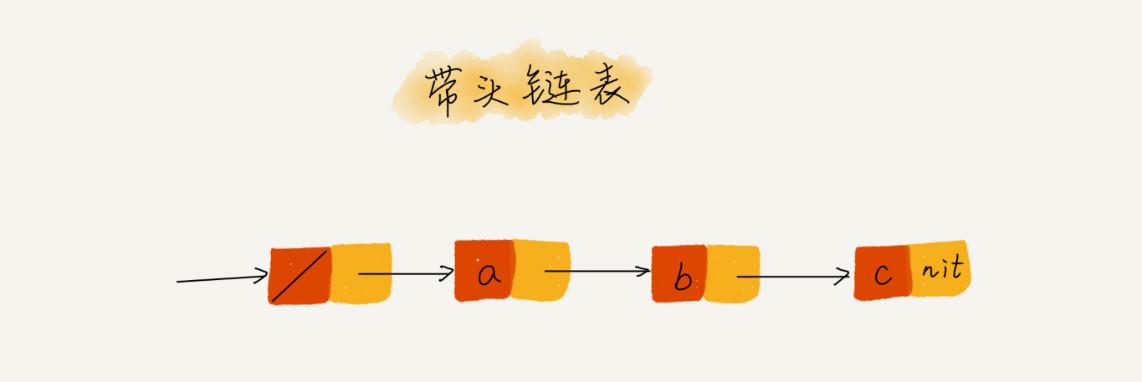
参考以下两段代码：

代码一：

// 在数组 a 中，查找 key，返回 key 所在的位置
// 其中，n 表示数组 a 的长度

int find(char* a, int n, char key) {
  // 边界条件处理，如果 a 为空，或者 n<=0，说明数组中没有数据，就不用 while 循环比较了
  if(a == null || n <= 0) {
    return -1;
  }

  int i = 0;
  // 这里有两个比较操作：i<n 和 a[i]==key.
  while (i < n) {
    if (a[i] == key) {
      return i;
    }
    ++i;
  }
  return -1;
}

代码二：

// 在数组 a 中，查找 key，返回 key 所在的位置
// 其中，n 表示数组 a 的长度
// 我举 2 个例子，你可以拿例子走一下代码
// a = {4, 2, 3, 5, 9, 6}  n=6 key = 7
// a = {4, 2, 3, 5, 9, 6}  n=6 key = 6

int find(char* a, int n, char key) {

  if(a == null || n <= 0) {
    return -1;
  }

  // 这里因为要将 a[n-1] 的值替换成 key，所以要特殊处理这个值
  if (a[n-1] == key) {
    return n-1;
  }

  // 把 a[n-1] 的值临时保存在变量 tmp 中，以便之后恢复。tmp=6。
  // 之所以这样做的目的是：希望 find() 代码不要改变 a 数组中的内容
  char tmp = a[n-1];

  // 把 key 的值放到 a[n-1] 中，此时 a = {4, 2, 3, 5, 9, 7}
  a[n-1] = key;

  int i = 0;
  // while 循环比起代码一，少了 i<n 这个比较操作
  while (a[i] != key) {
    ++i;
  }

  // 恢复 a[n-1] 原来的值, 此时 a= {4, 2, 3, 5, 9, 6}
  a[n-1] = tmp;

  if (i == n-1) {
    // 如果 i == n-1 说明，在 0...n-2 之间都没有 key，所以返回 -1
    return -1;
  } else {
    // 否则，返回 i，就是等于 key 值的元素的下标
    return i;
  }
}

在字符串 a 很长的时候，执行效率更高的是代码二。

因为代码二的字符串检索是比代码一少了一个判断。

• 代码一：O(2n)

• 代码二：O(n)

  • 代码一比代码 二多了个字符串最大限度遍历限制。
  • 备份字符串最后一个字符，并把其改为遍历结束标志。
  • 完成遍历后再恢复该字符。

注意：上面代码只是给个例子，实际开发中，若不追求极致效率，为了代码可读性，不建议上面这个代码的实现。

边界条件处理

在处理链表时，先用大脑走一遍，主要是边界问题，如：

• 链表为空时，代码是否正常工作？
• 链表只有一个节点时，代码是否正常工作？
• 链表有两个节点时，代码是否正常工作？
• 处理链表第一个节点或最后一个节点时，代码是否正常工作？

数据结构&算法-双向链表

双向链表

双向链表也是链表的一种，它每个数据结点中都有两个结点，分别指向其直接前驱和直接后继。所以我们从双向链表的任意一个结点开始都可以很方便的访问其前驱元素和后继元素。

代码

using System;

namespace DoubleLinkedList

    class Program
    
        static void Main(string[] args)
        
            DoubleLink<string> doubleLink = new DoubleLink<string>("头");
            doubleLink.AddNode(1, new Node<string>("第一名"));
            doubleLink.AddNode(1, new Node<string>("第5名"));
            doubleLink.AddNode(1, new Node<string>("第4名"));
            doubleLink.AddNode(1, new Node<string>("第9名"));
            doubleLink.AddNode(3, new Node<string>("第9名"));
            doubleLink.RemoveNode(4);
            doubleLink.AmendData(2, "被修改的");
            doubleLink.TraversingList();
        
    

    /// <summary>
    /// 结点
    /// </summary>
    class Node<T>
    
        public Node<T> next;
        public Node<T> last;
        T content;

        public Node(T content)
        
            this.content = content;
        
        public void AmendData(T amend)
        
            content = amend;
        
        public T GetContent()
        
            return content;
        
    
    class DoubleLink<T>
    
        Node<T> head; //头部不算个数，索引为0
        public DoubleLink(T t)
        
            head = new Node<T>(t);
        

        int NodeNum = 0;

        /// <summary>
        /// 添加结点
        /// </summary>
        /// <param name="index"></param>
        /// <param name="node"></param>
        public void AddNode(int index, Node<T> node)
        
            if (index < 1 || index > NodeNum + 1)
            
                return;
            
            Node<T> needNode = head;

            if (index == NodeNum + 1)
            
                for (int i = 0; i < NodeNum; i++)
                
                    needNode = needNode.next;
                
                needNode.next = node;
                node.last = needNode;
                NodeNum++;
            
            else
            
                for (int i = 0; i < index; i++)
                
                    needNode = needNode.next;
                
                needNode.last.next = node;
                node.last = needNode.last;
                node.next = needNode;
                needNode.last = node;
                NodeNum++;
            
        

        /// <summary>
        /// 删除结点
        /// </summary>
        /// <param name="index"></param>
        public void RemoveNode(int index)
        
            if (index < 1 || index > NodeNum)
            
                return;
            

            Node<T> needNode = head;
            for (int i = 0; i < index; i++)
            
                needNode = needNode.next;
            
            needNode.last.next = needNode.next;
            if (needNode.next != null)
            
                needNode.next.last = needNode.last;
                needNode.next = null;
            

            needNode.last = null;
            needNode = null;
        

        /// <summary>
        /// 查询结点
        /// </summary>
        /// <param name="index"></param>
        /// <returns></returns>
        public Node<T> GetNode(int index)
        
            if (index < 1 || index > NodeNum)
            
                return null;
            
            Node<T> needNode = head;
            for (int i = 0; i < index; i++)
            
                needNode = needNode.next;
            
            return needNode;
        

        public Node<T> AmendData(int index, T content)
        
            if (index < 1 || index > NodeNum)
            
                return null;
            
            Node<T> needNode = head;
            for (int i = 0; i < index; i++)
            
                needNode = needNode.next;
            
            needNode.AmendData(content);
            return needNode;
        

        /// <summary>
        /// 遍历链表
        /// </summary>
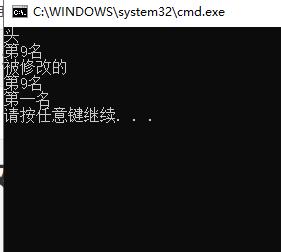
        public void TraversingList()
        
            Node<T> curNode = head;
            while (curNode != null)
            
                Console.WriteLine(curNode.GetContent());
                curNode = curNode.next;
            
        
    

参考【数据结构】之双向链表、双端(双向)链表、循环(双向)链表