微积分
定义
微分
给定一个 \\(x\\),微分表示 \\(x\\) 变化时 \\(y\\) 的变化。\\(\\mathrm dx\\) 表示 \\(x\\) 的变化量。
\\(\\mathrm{d}y\\) 称为微元。
\\(\\mathrm{d}y=f\'(x)\\mathrm{d}x\\)
如 \\(\\mathrm{d}(\\sin x)=(\\sin x)\'\\mathrm{d}x=\\cos x\\mathrm{d}x\\)
又发现 \\(f\'(x)=\\dfrac{\\mathrm{d}y}{\\mathrm{d}x}\\)
导数是微元和 \\(\\mathrm{d}x\\) 的商,所以导数有时又被称为微商。
积分
微分用来求出某个已知函数的导函数,而积分是微分的逆运算,是找到一个函数使得它的导函数是某个已知函数。这个函数就是已知函数的原函数。
一般将 \\(f(x)\\) 认为是导函数,\\(F(x)\\) 是其原函数。
例如 \\(F(x)=-\\frac12\\cos2x\\) 是 \\(f(x)=\\sin2x\\) 在 \\((-\\infty,+\\infty)\\) 上的原函数。
定理1
若函数 \\(f\\) 在区间 \\(I\\) 上连续,则 \\(f\\) 在 \\(I\\) 上存在原函数 \\(F\\).
定理2
若 \\(F\\) 是 \\(f\\) 在区间 \\(I\\) 上的原函数,则
\\((i) F+C\\) 也是 \\(f\\) 在区间 \\(I\\) 上的原函数,其中 \\(C\\) 为任意常数.
\\((ii) f\\) 在 \\(I\\) 上的任意两个原函数之间,只可能相差一个常数.
不定积分
函数 \\(f\\) 在区间 \\(I\\) 上的全体原函数称为 \\(f\\) 在 \\(I\\) 上的不定积分,记做
\\[\\int f(x)\\mathrm dx.
\\]
若 \\(F\\) 是 \\(f\\) 的一个原函数,则 \\(f\\) 的不定积分是一个函数群 \\(|F+C|\\),写作
\\[\\int f(x)\\mathrm dx=F(x)+C.
\\]
有
\\[[\\int f(x)\\mathrm dx]\'=f(x)\\\\\\mathrm d\\int f(x)\\mathrm dx=f(x)\\mathrm dx
\\]
其中,\\(d\\) 是微分运算.
基本积分表
大部分积分都难以计算,我们只能将其转换成一些已知的积分。
\\[\\begin{align*}
&1.\\int0\\mathrm dx=C.\\\\
&2.\\int1\\mathrm dx=\\int\\mathrm dx=x+C.\\\\
&3.\\int x^a\\mathrm dx=\\dfrac{x^{a+1}}{a+1}+C(a\\ne-1,x>0).\\\\
&4.\\int\\dfrac1x\\mathrm dx=\\ln |x|+C(x\\ne0).\\\\
&5.\\int e^x\\mathrm dx=e^x+C.\\\\
&6.\\int a^x\\mathrm dx=\\dfrac{a^x}{\\ln a}+C(a>0,a\\ne1).\\\\
&7.\\int\\cos ax\\mathrm dx=\\dfrac1a\\sin ax+C(a\\ne0).\\\\
&8.\\int\\sin ax\\mathrm dx=-\\dfrac1a\\cos ax+C(a\\ne0).\\\\
&9.\\int\\sec^2x\\mathrm dx=\\tan x+C.\\\\
&10.\\int\\csc^2x\\mathrm dx=-\\cot x+C.\\\\
&11.\\int\\sec x\\cdot\\tan x\\mathrm dx=\\sec x+C.\\\\
&12.\\int\\csc x\\cdot\\cot x\\mathrm dx=-\\csc x+C.\\\\
&13.\\int\\dfrac{\\mathrm dx}{\\sqrt{1-x^2}}=\\arcsin x+C=-\\arccos x+C_1.\\\\
&14.\\int\\dfrac{\\mathrm dx}{1+x^2}=\\arctan x+C=-\\arccot x+C_1.\\\\
\\end{align*}
\\]
但像 \\(\\ln x,\\tan x\\) 等基本初等函数,现在仍然没有求出他们的原函数。
不定积分线性法则
若 \\(f\\) 与 \\(g\\) 在区间 \\(I\\) 上都存在原函数,\\(k_1,k_2\\) 是两个任意常数,则 \\(k_1f+k_2g\\) 在区间 \\(I\\) 上也存在原函数,且
\\[\\int[k_1f(x)+k_2g(x)]\\mathrm dx=k_1\\int f(x)\\mathrm dx+k_2\\int g(x)\\mathrm dx.
\\]
证:
\\[\\begin{align*}
[k_1\\int f(x)\\mathrm dx+k_2\\int g(x)\\mathrm dx]\'&=k_1(\\int f(x)\\mathrm dx)\'+k_2(\\int f(x)\\mathrm dx)\'\\\\
&=k_1f(x)+k_2g(x).
\\end{align*}
\\]
线性法则的一般形式为
\\[\\int(\\sum_{i=1}^nk_if_i(x))\\mathrm dx=\\sum_{i=1}^n(k_i\\int f_i(x)\\mathrm dx).
\\]
由此可以将一个积分拆开来分别积分然后相加得到原积分.
例
\\[\\begin{align*}
\\int(10^x-10^{-x})^2\\mathrm dx&=\\int(10^{2x}+10^{-2x}-2)\\mathrm dx\\\\
&=\\int[(10^2)^x+(10^{-2})^x-2]\\mathrm dx\\\\
&=\\dfrac{(10^2)^x}{\\ln (10^2)}+\\dfrac{(10^{-2})^x}{\\ln (10^{-2})}-2x+C\\\\
&=\\dfrac{1}{2\\ln 10}(10^{2x}-10^{-2x})-2x+C.
\\end{align*}
\\]
\\[\\int(1-x+x^3-\\frac{1}{\\sqrt[3]{x^2}})\\mathrm dx=x-\\frac12x^2+\\frac14x^4-3x^{\\frac13}+C.
\\]
\\[\\int(2^x+3^x)\\mathrm dx=\\frac{1}{\\ln 4}4^x+\\frac{2}{\\ln 6}6^x+\\frac{1}{\\ln 9}9^x+C.
\\]
\\[\\begin{align*}
\\int\\sin^2x\\mathrm dx&=\\frac12\\int2\\sin^2\\mathrm dx\\\\
&=\\frac12\\int(1-\\cos2x)\\mathrm dx\\\\
&=\\frac12(x-\\frac12\\sin2x)+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int\\frac{\\cos2x}{\\cos^2x\\cdot\\sin^2x}\\mathrm dx&=\\int\\frac{\\cos^2x-\\sin^2x}{\\cos^2x\\cdot\\sin^2x}\\mathrm dx\\\\
&=\\int(\\frac{1}{\\sin^2x}-\\frac{1}{\\cos^2x})\\mathrm dx \\\\
&=\\int(\\csc^2x-\\sec^2x)\\mathrm dx \\\\
&=-\\cot x-\\tan x+C.
\\end{align*}
\\]
换元积分法
感性理解:就是把前面的一些项放进后面的 \\(\\mathrm dx\\) 里,使 \\(\\mathrm dx\\) 变成前面剩下的式子的形式,或者把前面的项变成 \\(\\mathrm d\\) 里面的项的形式。
前者称为第一换元积分法,后者称为第二换元积分法。
注意到 \\(d(f)=f\'\\mathrm dx\\).
例
- 求 \\(\\int\\tan x\\mathrm dx.\\)
\\[\\int\\tan x\\mathrm dx=\\int\\frac{\\sin x}{\\cos x}\\mathrm dx
\\]
由 \\(-\\sin x\\mathrm dx=\\mathrm d(\\cos x)\\)
则
\\[\\begin{align*}
\\int\\frac{\\sin x}{\\cos x}\\mathrm dx&=-\\int\\frac{1}{\\cos x}\\mathrm d(\\cos x)\\\\
&=-\\ln|\\cos x|+C.
\\end{align*}
\\]
- 求 \\(\\int\\frac{\\mathrm dx}{a^2+x^2}(a>0).\\)
\\[\\begin{align*}
\\int\\frac{\\mathrm dx}{a^2+x^2}&=\\int\\frac{(\\dfrac1a)^2\\mathrm dx}{1+(\\dfrac xa)^2}\\\\
&=\\frac1a\\int\\frac{\\mathrm d(\\dfrac xa)}{1+(\\dfrac xa)^2}\\\\
&=\\frac1a\\arctan\\frac xa+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int\\cos(3x+4)\\mathrm dx&=\\frac13\\int\\cos(3x+4)\\mathrm d(3x+4)\\\\
&=\\frac13\\sin(3x+4)+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int xe^{2x^2}\\mathrm dx&=\\int xe^{2x^2}\\frac{\\mathrm d(2x^2)}{4x}\\\\
&=\\frac14\\int e^{2x^2}\\mathrm d(2x^2)\\\\
&=\\frac14e^{2x^2}+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int\\frac{\\mathrm dx}{2x+1}&=\\frac12\\int\\frac{\\mathrm d(2x+1)}{2x+1}\\\\
&=\\frac12\\ln|2x+1|+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int(1+x)^n\\mathrm dx&=\\int(1+x)^n\\mathrm d(1+x)\\\\
&=\\frac{(1+x)^{n+1}}{n+1}+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int\\frac{\\mathrm dx}{\\sqrt[3]{7-5x}}&=-\\frac15\\int(7-5x)^{-\\frac13}\\mathrm d(7-5x)\\\\
&=-\\frac{3}{10}(7-5x)^{\\frac23}+C.
\\end{align*}
\\]
分部积分法
由乘积求导法,可以导出分布积分法。
定理:若 \\(u(x)\\) 和 \\(v(x)\\) 可导,不定积分 \\(\\int u\'(x)v(x)\\mathrm dx\\) 存在,则 \\(\\int u(x)v\'(x)\\mathrm dx\\) 也存在,并有:
\\[\\int u(x)v\'(x)\\mathrm dx=u(x)v(x)-\\int u\'(x)v(x)\\mathrm dx.
\\]
证:由
\\[[u(x)v(x)]\'=u\'(x)v(x)+u(x)v\'(x)
\\]
两边求不定积分,得到:
\\[u(x)v(x)=\\int u(x)v\'(x)\\mathrm dx+\\int u\'(x)v(x)\\mathrm dx,\\\\
\\int u(x)v\'(x)\\mathrm dx=u(x)v(x)-\\int u\'(x)v(x)\\mathrm dx.
\\]
即为上式.
这个公式称为分部积分公式,注意到 \\(d(f)=f\'\\mathrm dx\\),这个公式常简写作
\\[\\int u\\mathrm dv=uv-\\int v\\mathrm du.
\\]
利用该式计算积分即为分部积分法。
例
- 求 \\(\\int \\arcsin x\\mathrm dx\\)
此处看到一个隐函数求导的方法:求\\((\\arcsin x)\'\\)
令 \\(y=\\arcsin x\\),则 \\(\\sin y=x\\),把 \\(\\sin y\\) 看做复合函数,对两边求导得
\\(\\cos y\\cdot y\'=1\\),则 \\(y\'=\\dfrac{1}{\\cos y}=\\dfrac{1}{\\sqrt{1-\\sin^2 y}}=\\dfrac{1}{\\sqrt{1-x^2}}\\)
所以 \\((\\arcsin x)\'=\\dfrac{1}{\\sqrt{1-x^2}}\\)
那么
\\[\\begin{align*}
\\int \\arcsin x\\mathrm dx&=x\\arcsin x-\\int x\\mathrm d(\\arcsin x)\\\\
&=x\\arcsin x-\\int \\frac{x}{\\sqrt{1-x^2}}\\mathrm dx\\\\
&=x\\arcsin x-\\int x(1-x^2)^{-\\frac12}\\frac{\\mathrm d(1-x^2)}{-2x}\\\\
&=x\\arcsin x+\\frac12\\int(1-x^2)^{-\\frac12}\\mathrm d(1-x^2)\\\\
&=x\\arcsin x+\\frac12\\frac{(1-x^2)^{\\frac12}}{\\frac12}\\\\
&=x\\arcsin x+(1-x^2)^{\\frac12}+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int \\ln x\\mathrm dx&=x\\ln x-\\int x\\mathrm d(\\ln x)\\\\
&=x\\ln x-\\int\\mathrm dx\\\\
&=x\\ln x-x+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int x^2\\cos x\\mathrm dx&=\\int x^2\\mathrm d(\\sin x)\\\\
&=x^2\\sin x-\\int\\sin x\\mathrm d(x^2)\\\\
&=x^2\\sin x-2\\int x\\sin x\\mathrm dx\\\\
&=x^2\\sin x+2\\int x\\mathrm d(\\cos x)\\\\
&=x^2\\sin x+2(x\\cos x-\\int \\cos x\\mathrm dx)\\\\
&=x^2\\sin x+2(x\\cos x-\\sin x)\\\\
&=x^2\\sin x+2x\\cos x-2\\sin x+C.
\\end{align*}
\\]
\\[\\begin{align*}
\\int \\frac{\\ln x}{x^3}\\mathrm dx&=\\int x^{-3}\\ln x\\mathrm dx\\\\
&=-\\frac12\\int\\ln x\\mathrm d(x^{-2})\\\\
&=-\\frac12(x^{-2}\\ln x-\\int x^{-2}\\mathrm d(\\ln x))\\\\
&=-\\frac12(x^{-2}\\ln x-\\int x^{-3}\\mathrm dx)\\\\
&=-\\frac12(x^{-2}\\ln x-\\frac12x^{-2})\\\\
&=\\frac{\\frac12-\\ln x}{2x^2}+C.
\\end{align*}
\\]
定积分
不定积分是求导的逆运算,定积分则是某种特殊和式的极限,他们本质不同,但形式类似,又有伟大的牛顿-莱布尼茨公式,所以我们可以用解不定积分的方法来解决定积分的问题。
定积分一个经典的运用是求函数图形面积。
我们计算一个函数 \\(f\\) 的一部分与 \\(x\\) 轴,和两条直线的封闭图形的面积,将 \\(\\mathrm dx\\) 视作横坐标的变化量,将 \\(f(x)\\) 视作高度,当 \\(\\mathrm dx\\) 无穷小时,该图形面积可以表示为
\\[\\int_a^bf(x)\\mathrm dx,
\\]
由牛顿-莱布尼茨公式,有
\\[\\int_a^bf(x)\\mathrm dx=F(b)-f(a)=F(x)|_a^b.
\\]
计算图形面积
- 求 \\(y=\\dfrac1x\\) 从 \\(1\\) 到 \\(2\\) 与 \\(x\\) 轴围成的面积
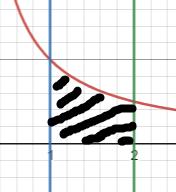
即为
\\[\\int_1^2\\frac1x\\mathrm dx=\\ln x|_1^2=\\ln2-\\ln1=\\ln2
\\]
- 求 \\(y=\\sin x\\) 从 \\(0\\) 到 \\(\\pi\\) 的面积
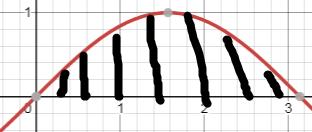
即为
\\[\\int_0^\\pi\\sin x\\mathrm dx=-\\cos x|_0^\\pi=-\\cos\\pi+\\cos0=2
\\]
推导圆的面积公式:
求 \\(\\frac14\\) 圆的面积
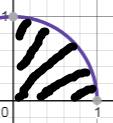
即为
\\[\\begin{align*}
\\int_0^r\\sqrt{r^2-x^2}\\mathrm dx&=\\frac12r^2\\arcsin\\frac xr+x\\sqrt{r^2-x^2}|_0^r\\\\
&=\\frac{\\pi r^2}{4}-0\\\\
&=\\frac{\\pi r^2}{4}
\\end{align*}
\\]
所以圆面积公式为 \\(4\\times \\dfrac{\\pi r^2}{4}=\\pi r^2\\)
牛顿从力学出发,莱布尼茨从哲学出发,几乎同时都发明了类似的工具。任何重大发明的过程中,时间早远没有我们想象的重要。微积分最原始的思想,牛顿的老师巴罗就已经考虑过,但是那不能算是微积分。


