美团的测试面试题，真的很难吗？

Posted 2021-11-03 程序员二黑

年前，我的一个粉丝留言给我说，他在面试美团的自动化测试岗的时候，不幸挂掉了。

年前，我的一个粉丝留言给我说，他在面试美团的自动化测试岗的时候，不幸挂掉了。

越想越可惜，回想面试经过，好好总结了几个点，发现面试没过的主要原因是在几个关键的问题没有给到面试官想要的答案

美团的面试会问些什么问题呢？他给我的留言是这样的：

• 根据你的工作经历，说说你对质量保证的理解？
• 非关系型数据库和关系型数据库的区别，谈谈他们的优势？
• 在自动化方面有什么成熟的方案，有没有做过二次开发？
• 质量部如果需要定制化一个质量体系平台，你会考虑哪些问题？

以上问题，如果是你，你会怎么回答？【文末答案】

前几年的测试行业还是一个风口，随着不断地转行人员以及毕业的大学生疯狂地涌入软件测试行业，目前测试行业“缺口”已经基本饱和。当然，我说的是最基础的功能测试的岗位需求已经很少了，而自动化、性能、安全乃至于以后可能出现的大数据测试、AI测试仍存在着非常多的机会。

“长江后浪推前浪，前浪死在沙滩上”，曾经一句让人会心一笑的调侃，如今变成了测试行业的真实写照。由于测试行业入门门槛低，薪资报酬高，不断有新鲜血液冲刷着测试行业的“前行者”们，给我们带来了非常大的压力。

那些入行几年，但是依然是功能测试的同学所面临的的压力可想而知。说到底，软件测试还是属于技术岗位。既然是技术岗位，那就要靠技术说话。不断掌握新的技能，提高业务能力也就变成了目前测试人迫在眉睫需要解决的问题。因此，现在大部分初级功能测试人员都在向自动化、性能、安全靠拢。

但是还是有不少的软件测试工程师站在“十字路口”迷茫、无助，找不到自己的方向。

一切的迷茫都是因为想得太多，而做的太少！每个测试行业从业者都能意识到目前自己面临的窘境，但能及时作出改变，顺应时代变化的人还是太少。多数人明明“泰山崩于前而面色如土”却只能眼睁睁看着自己被行业淘汰吗？

并不是，下面这份测试工程师发展规划路线，会给你带来灵感和方向：

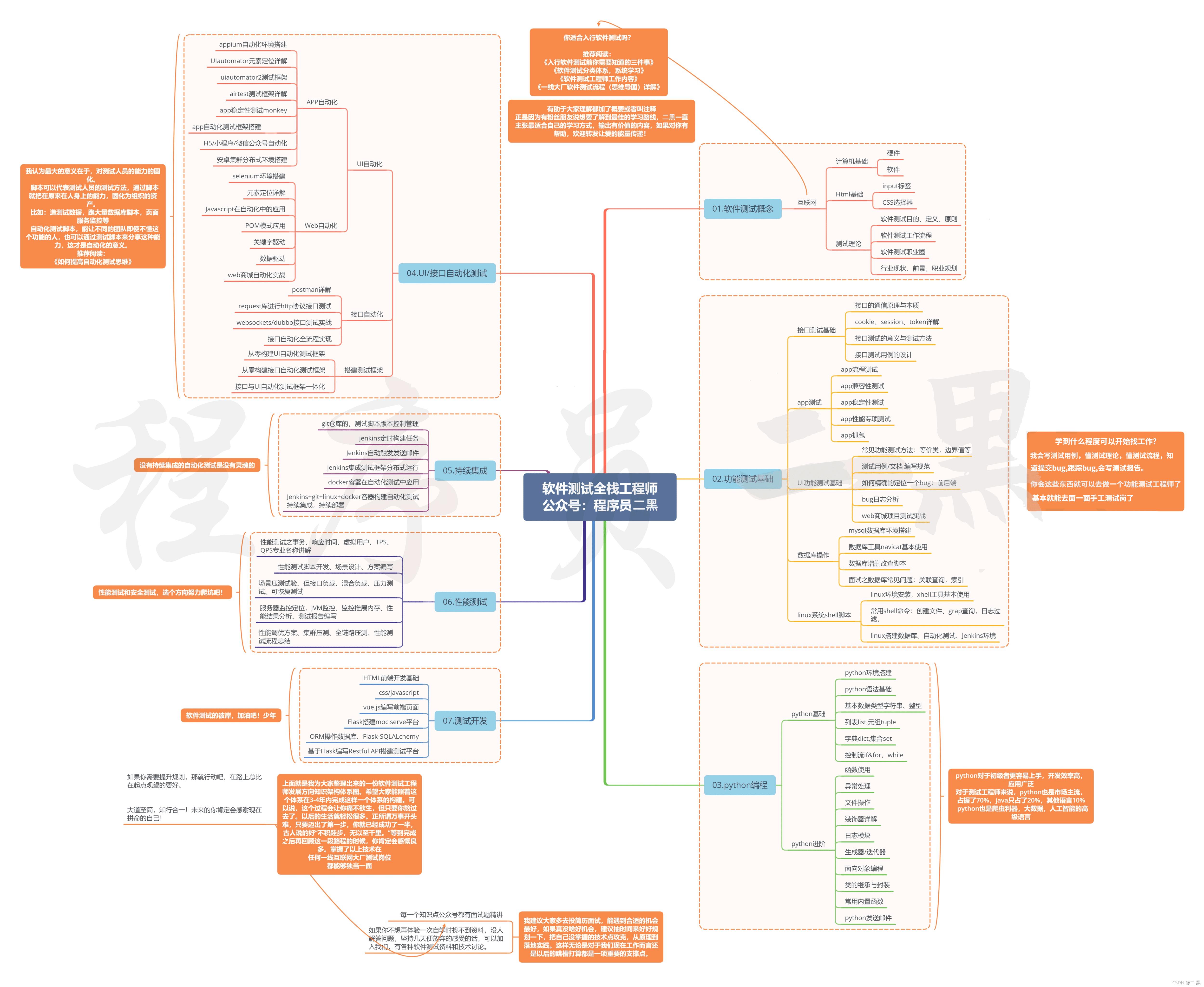
上面就是我为大家整理出来的一份软件测试工程师发展方向知识架构体系图。希望大家能照着这个体系在3-4年内完成这样一个体系的构建。可以说，这个过程会让你痛不欲生，但只要你熬过去了。以后的生活就轻松很多。正所谓万事开头难，只要迈出了第一步，你就已经成功了一半，古人说的好“不积跬步，无以至千里。”等到完成之后再回顾这一段路程的时候，你肯定会感慨良多。

如果你不想再体验一次自学时找不到资料，没人解答问题，坚持几天便放弃的感受的话，可以加我们群：785128166，一起讨论，里面有各种软件测试资料和技术交流。

上文问题【附答案】

1.根据你的工作经历，说说你对质量保证的理解？

这是个综合性基础知识问题，考验你在测试行业工作几年后的心得，是否有测试思维，明确自己的定位。可以谈谈你认为如何做好测试？如何衡量质量？你又如何专注软件质量提升，帮助团队快速迭代高质量交付

2.非关系型数据库和关系型数据库的区别，谈谈他们的优势？

数据库在测试工作中的重要性相信我就不用在这赘述了，需要你对常见的关系型数据库和非关系型数据库的原理理解，而且总结出它们之前的区别

3.在自动化方面有什么成熟的方案，有没有做过二次开发？

测试工程师离不开一个关键字，“自动化”，在任何类型的项目或多或少会用到自动化测试技术。关于前后端自动化技术，是否有一套完整的测试框架，技术体系。在开源自动化测试框架的理解上，有一定的开发思维，能进行封装，开源框架上二次开发。能根据项目灵活打造适合团队的测试框架，是测试工程师的能力分水岭

4.质量部如果需要定制化一个质量体系平台，你会考虑哪些问题？

说实话，面试官这么问测试平台的问题，你可能就扛不住了。干过测试开发的应该都知道，测试平台的构造，除了技术难点。你要考虑如何去推进这个工作？测试平台研发出来后，在整个测试部门推广运营这个平台是大难题。在功能测试人员的角度来想，去使用不成熟的测试平台来测试，如果加大你的工作量，对你自身工作和技术没有什么太大价值，一般都不是非常积极的去配合，测试平台如何推广运营是个难题。你要让所有人亲身感受到用与不用这个测试平台有什么区别。

最后也给软件测试的朋友们分享一份测试资料：

以上内容，对于软件测试的朋友来说应该是最全面最完整的备战仓库了，为了更好地整理每个模块，我也参考了很多网上的优质博文和项目，力求不漏掉每一个知识点，很多朋友靠着这些内容进行复习，拿到了BATJ等大厂的offer，这个仓库也已经帮助了很多的软件测试的学习者，希望也能帮助到你。加群：785128166，免费获取！

机会只垂青有准备的人，这是一个靠本事的社会。有时候，你之所以发展得不好，不是因为没有机遇，而是因为你没有准备好，导致机遇与你擦肩而过。如果你想要学习，什么时候开始都不晚，而不是瞻前顾后，你只要用尽全力，剩下的交给时间！

加油吧，测试人！路就在脚下，成功就在明天！

记一个美团的二分查找面试题

今天分享一道有趣的二分查找的题目，这也是美团面试遇到的比较难的一题，让我们一起看看怎么去解决它。

连续段最大的中位数

先看看问题：

牛牛得到了一个长度为n的正整数序列，现在牛牛想要从里面取出一段连续的长度大于等于k的序列。
定义一个序列的“中数”为最大的整数x，使得序列中至少一半的数字大于等于x
牛牛想知道这个取出来的序列的中数最大可以是多少？

其实问题本身就有点难理解，当时我读这道题读了好几遍都不太明白题目想表达的含义。我们配合提供的示例来说明下这个题目是什么意思。

输入：5,3,[30,1,2,31,9]  
输出：30  
说明：选前四个数字组成[30,1,2,31]，中数为30

我们以示例来说明，n=5为数组的长度，k=3是要取出序列的最小长度。那么第一件事情，我们可以枚举出所有的序列，分别是

• [30,1,2]

• [1,2,31]

• [2,31,9]

• [30,1,2,31]

• [1,2,31,9]

• [30,1,2,31,9]  

我们共计可以枚举出六个序列。然后再来看什么是中位数。对于每一个序列来说，如果有一个数字能够让序列中一半的数字都大于等于它，那么这个数字就是这个序列的中位数。换句话说我们对数组排序，取下标是n>>1的数字，他就是中位数。

再回到上面的六个序列

• [30,1,2] 中位数是2

• [1,2,31] 中位数是2

• [2,31,9] 中位数是9

• [30,1,2,31] 中位数是30

• [1,2,31,9] 中位数是9

• [30,1,2,31,9] 中位数是9  

因此这六个序列中最大的中位数就是30，也就是本体的答案说明。

暴力法

最直观的解法就是暴力法，我们枚举所有可能的序列，然后算出中位数，取最大的一个即可。但是这种必然面临着超时的问题，由于暴力法比较简单我们就不写代码了。

二分查找

回顾一下二分查找的运用场景，最简单的莫过于猜数字。例如主持人在0-100中想一个数让参赛者来猜，第一次参赛者猜50，根据主持人的反馈猜的这个数字偏大还是偏小，继而猜下个数字。如果主持人想的数字比50大，那么这个数字必然在50-100之间，那么参赛者会猜75；如果比50小，那么参赛者会猜25。这就是二分查找的应用场景之一。

再比如之前提到的自己实现一个简单的开平方功能。我们在0到目标值中间取平均值，判断这个平均值平方以后和目标值的关系，继而来调整范围。

所以根据以上两个场景我们可以总结出二分查找的步骤：

1. 找出答案的上下限，假如答案是ans，a是下限，b是上限，满足a<=ans<=b。

2. 算出ab的平均值，判断平均值和目标值的关系。例如猜数字中会判断平均值和目标值是大还是小；在开方题目中，则是判断平均值的平方和目标值的关系。

3. 根据2中的关系，来更改a或者b的取值，从而缩小范围。循环1，2步。

4. 如果a和b相等或者差值在很小的误差范围内，那么可认为已经找到所需的答案了。

回到题目，我们可以类比的列出解这道题的思路步骤：  

1. 因为答案必然在数组中，我们可以将下限设定为数组中最小的数，上限设定为数组中最大的数。

2. 这一步是比较难的，如果关系想清楚了，那么这道题就迎刃而解了。假如我们有一个平均值，这个平均值在数组的某个序列中是中位数，那么我们可以认为下限还可以继续增大，如果这个数字不是任何序列的中位数，那么可以认为上限应该降低。所以这道题的关键在于怎么比较高效的遍历所有序列去确定平均值是不是中位数。

3. 如果调整下限，可令新的下限是mid+1；如果调整上限，可令新的上限是mid-1。

4. 如果上下限重叠或者下限超过了上限，那么可认为找到答案。

1.找到上下限，很简单：

int max = Integer.MIN_VALUE;
    int min = Integer.MAX_VALUE;
    for (int i = 0; i < n; i++) {
      max = Math.max(a[i], max);
      min = Math.min(a[i], min);
    }

2.如何去匹配关系

while (l <= r) {
      // 中间的数
      int mid = (l + r) >> 1;
      //比中位数大的数
      int greaterThanMidCount = 0;
      // 先看mid在前面0到k-1个数字中是否是中位数
      for (int i = 0; i < k; i++) {
        if (a[i] >= mid) {
          //大于等于中位数，则数量+1
          greaterThanMidCount++;
        } else {
          greaterThanMidCount--;
        }
      }
      // 说明mid可以增加
      if (greaterThanMidCount >= 0) {
        ans = mid;
        l = mid + 1;
        continue;
      }
      // 如果在前面k个数字中，mid无法成为它们的中位数才会走到这里

      boolean flag = false;
      int cur = 0;
      int ps = 0;
      // 继续从第k+1个数字看
      for (int i = k; i < n; i++) {
        if (a[i] >= mid) {
          greaterThanMidCount++;
        } else {
          greaterThanMidCount--;
        }
        /*
         * 滑动窗口，靠这个去高效遍历其他序列
         * 这里从头去除元素，模拟滑动窗口
         */
        if (a[i - k] >= mid) {
          /*
           * 如果大于等于mid，可以认为去除这个数字后，
           * 新的序列中将会减少一个大于等于mid的数字，
           * 从而减小让mid成为中位数的概率
           */
          cur++;
        } else {
          /*
           * 如果小于mid，可以认为去除这个数字后，
           * 新的序列中将会减少一个小于mid的数字，
           * 从而增加让mid成为中位数的概率
           */
          cur--;
        }
        /* ps为记录上次 从头开始看 比mid数小的数字所记录的一个浮标
         * 这个值越小，mid成为中位数的概率就越大。换句话说要尽可能让
         * mid成为中位数，不断的提高下限
         */
        ps = Math.min(ps, cur);

        /*
          判断去除头部元素后 还能否是中位数
         */
        if (greaterThanMidCount - ps >= 0) {
          flag = true;
          break;
        }
      }
      // 还是可以找到以mid为中点的大于等于k的一段序列
      if (flag) {
        ans = mid;
        //提高下限
        l = mid + 1;
      } else {
        //减少上限
        r = mid - 1;
      }
    }

这一段代码有点晦涩难以理解，需要多看几遍。但是总体思想就是让mid尽可能的成为中位数，有点类似贪心算法局部最优推导出全局最优，但是这个推导过程没有说明，需要再斟酌下。

The    end

Cool Coding

喜欢就关注我，和我一起玩吧～