Codeforces Round #751 (Div. 2)

Posted 2021-11-02 zhy-cx

Codeforces Round #751 (Div. 2)

A. Two Subsequences

思路分析：

• x实际上就是字符串里最小的字符。
• 剩下的便是y。

代码

#include <bits/stdc++.h>
using namespace std;

int main()
{
        ios::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
        int t;
        cin >> t;
        while (t--)
        {
                string s;
                cin >> s;
                char ch = \'z\';
                int pos = 0;
                for (int i = 0; i < s.size(); i++)
                {
                        if (s[i] < ch)
                        {
                                pos = i;
                                ch = s[i];
                        }
                }
                cout << ch << \' \';
                for (int i = 0; i < s.size(); i++)
                {
                        if (i != pos)
                        {
                                cout << s[i];
                        }
                }
                cout << endl;
        }
        return 0;
}

B. Divine Array

思路分析：

• 这题我想复杂了，实际上不需要像我这么麻烦（比赛时的代码太复杂了，就不放了），因为不管怎么样，进行\\(1000\\)轮后都不会再进行改变。
• 所以我们对于每一个序列都操作1000次，然后储存答案，查询时间就是O(1)，当然，算法主体时间是O(1000 * \\(n^2\\))。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000;
vector<int> v[maxn];

int main()
{
        int t;
        cin >> t;
        while (t--)
        {
                int n;
                cin >> n;
                for (int i = 1; i <= n; i++)
                {
                        int x;
                        cin >> x;
                        v[0].push_back(x);
                }
                int i;
                for (i = 1;; i++)
                {
                        int flag = 0;
                        for (int j = 0; j < n; j++)
                        {
                                int t = count(v[i - 1].begin(), v[i - 1].end(), v[i - 1][j]);
                                v[i].push_back(t);
                                if (v[i][j] != v[i - 1][j])
                                {
                                        flag = 1;
                                }
                        }
                        if (!flag)
                        {
                                break;
                        }
                }
                int q;
                cin >> q;
                while (q--)
                {
                        int a, b;
                        cin >> a >> b;
                        if (b >= i)
                                cout << v[i][a - 1] << endl;
                        else
                                cout << v[b][a - 1] << endl;
                }
                for (int j = 0; j <= i; j++)
                {
                        v[j].clear();
                }
        }
        return 0;
}

C. Array Elimination

思路分析：

• 这题一开始没想法，最后猜了一下按位做，然后推了一下，发现确实有道理就写上了。
• 首先，对于每一位，看有多少个\\(1\\)，如果有\\(n\\)个\\(1\\)的话，那么只要选择\\(n\\)的因子个当前位为\\(1\\)的数即可（假如是\\(3\\)，那么只能选\\(1\\)或者\\(3\\)，如果是\\(4\\)，那么只能选\\(1\\)，\\(2\\),\\(4\\)，对于其他的数也是这样的，推一下就可以知道），那么我们对于每一位都是这样的操作的话，那么我们只需要求每一位\\(1\\)的个数的gcd的因子即可。
• 证明如下：
  

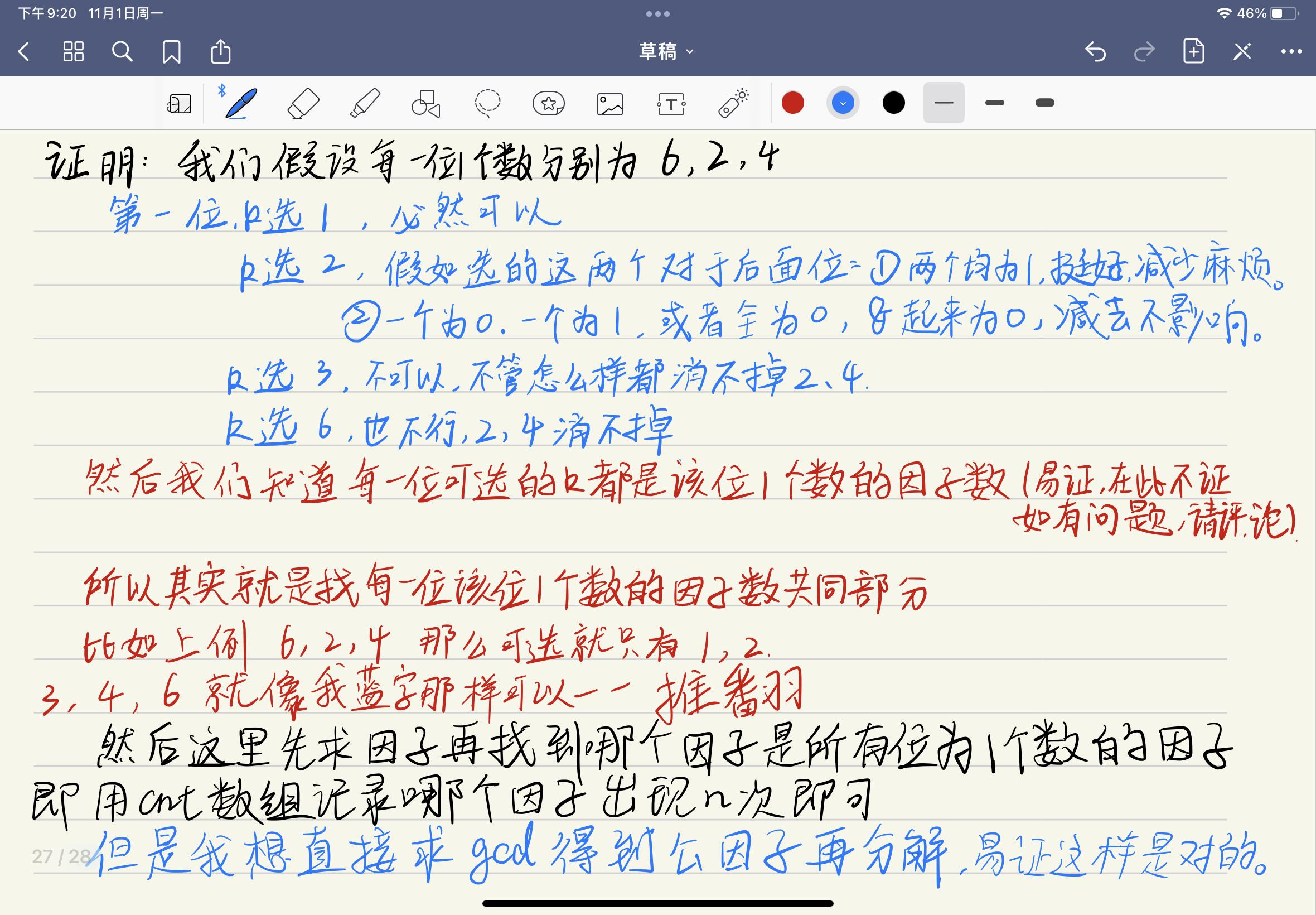
代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
int a[maxn];
int cnt[30];
int main()
{
        int t = read();
        while (t--)
        {
                for (int i = 0; i <= 29; i++)
                {
                        cnt[i] = 0;
                }
                int n = read();
                for (int i = 1; i <= n; i++)
                {
                        a[i] = read();
                }
                for (int j = 29; j >= 0; j--)
                {
                        for (int i = 1; i <= n; i++)
                        {
                                if ((a[i] >> j) & 1)
                                {
                                        cnt[j]++;
                                }
                        }
                }
                int gcd = 0;
                for (int j = 30; j >= 0; j--)
                {
                        gcd = __gcd(gcd, cnt[j]);
                }
                if (gcd == 0)
                {
                        for (int i = 1; i <= n; i++)
                        {
                                printf("%d ", i);
                        }
                }
                else
                {
                        vector<int> ans;
                        for (int i = 1; i <= gcd; i++)
                        {
                                if (gcd % i == 0)
                                {
                                        ans.push_back(i);
                                }
                        }
                        for (int i = 0; i < ans.size(); i++)
                        {
                                printf("%d ", ans[i]);
                        }
                }
                puts("");
        }
        return 0;
}

D. Frog Traveler

思路分析：

• 这题没想到可以用BFS，因为我们要求最小步数，所以在每一轮中保证了步数是一致的，并且我们可以知道，不可能往后退。
• 所以是线性的，每个位置只走一遍，具体看代码注释。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5 + 10;
int a[maxn], b[maxn];
//题目给的
int minh, n;
//我们把上一轮最大高度记录一下
int pre[maxn];
//记录当前位置的前面一个位置
int dis[maxn];
//记录步数
int ans[maxn];
//记录当前位置前面位置的答案
int bfs()
{
        queue<int> q;
        memset(pre, -1, sizeof(pre));
        memset(dis, 0x3f, sizeof(dis));
        memset(ans, 0, sizeof(ans));
        q.push(n);
        minh = n;
        dis[n] = 0;
        //初始化
        while (!q.empty())
        {
                int h = q.front();
                q.pop();
                if (h == 0)
                        return dis[h];
                //如果出现了0，那么直接return即可
                for (int x = a[h]; x > 0; x--)
                {
                        int now = h - x, temp = 0;
                        //now是指跳了x高的高度，temp用来储存跳完之后的高度
                        if (now >= minh)
                        {
                                break;
                        }
                        if (now > 0)
                        {
                                temp = now, now += b[now];
                                //now变成跳完之后掉下来的高度
                        }
                        else
                                now = 0;
                        if (dis[now] > dis[h] + 1)//如果当前高度之前没有枚举到
                        {
                                dis[now] = dis[h] + 1;
                                pre[now] = h;
                                //掉下来的高度的前驱为h
                                ans[now] = temp;
                                //掉下来的高度的前面位置的高度
                                q.push(now);
                        }
                }
                minh = min(minh, h - a[h]);
                //更新最低高度
        }
        return -1;
}
int main()
{
        ios::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
        cin >> n;
        for (int i = 1; i <= n; i++)
        {
                cin >> a[i];
        }
        for (int i = 1; i <= n; i++)
        {
                cin >> b[i];
        }
        minh = n;
        cout << bfs() << endl;
        stack<int> s;
        int x = 0;
        while (pre[x] != -1)
        {
                s.push(x);
                x = pre[x];
                //找前驱
        }
        while (!s.empty())
        {
                int now = s.top();
                cout << ans[now] << \' \';
                s.pop();
        }
        cout << endl;
        return 0;
}

Codeforces Round #436 E. Fire（背包dp+输出路径）

题意：失火了，有n个物品，每个物品有价值pi,必须在时间di前（小于di）被救，否则就要被烧毁。救某个物

　　　　品需要时间ti,问最多救回多少价值的物品，并输出救物品的顺序。

 

 

Examples

 

Input

3
3 7 4
2 6 5
3 7 6

 

Output

11
2
2 3 

 

Input

2
5 6 1
3 3 5

 

Output

 

1
1
1 

思路：有点像一个背包，dp数组记录的是当前时间所能获得的最大价值,转移方程dp[j]=max(dp[j],dp[j-t[i].ti]+t[i].w)
　　　　path[i][j]表示到i号物品j时间的状态时救的物品编号（这里是从0开始）
　　　　emmmmm 具体的在代码中加以注释。

代码：
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
const int maxn=2010;
struct node{
    int ti,en,w,op;
}t[110];
int dp[maxn],path[110][maxn],a[110];

bool cmp(node x,node y){
    if(x.en!=y.en)return x.en<y.en;
    else return x.ti<y.ti;
}


int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>t[i].ti>>t[i].en>>t[i].w;
        t[i].op=i+1;
        //op为每个物品的标号，题目要求从1开始 
    }
    memset(dp,0,sizeof(dp));
    memset(path,-1,sizeof(path));//开始全部置为-1 
    sort(t,t+n,cmp);
    int ma=0;
    for(int i=0;i<n;i++){
        ma=max(ma,t[i].en);
        if(i!=0){
            for(int j=0;j<t[i].ti;j++)path[i][j]=path[i-1][j];
            //时间小于所需的营救时间，那么就不救，等于上一状态 
        }
        for(int j=t[i].en-1;j>=t[i].ti;j--){
            if(dp[j]<dp[j-t[i].ti]+t[i].w){
                dp[j]=dp[j-t[i].ti]+t[i].w;
                path[i][j]=i;
                //如果救，那么就更新dp数组以及path数组为该物品 
            }
            else if(i>0){
                path[i][j]=path[i-1][j];
                //如果不救，那么还是等于上一状态 
            }
        }
    }
    int sum=0,temp=0;
    for(int i=0;i<=ma;i++){
        if(dp[i]>sum){
            sum=dp[i];
            temp=i;
            //取出最大价值以及在最大价值的情况下，救完最后一个物品的时间 
        }
    }
    int k=n-1,c=0;
    while(temp>0){
        a[c++]=t[path[k][temp]].op;
        temp-=t[path[k][temp]].ti;
        k--;
        k=path[k][temp];
        //反着记录下路径 
    }
    cout<<sum<<endl<<c<<endl;
    for(int i=c-1;i>=0;i--){
        if(i!=c-1)cout<<‘ ‘;
        cout<<a[i];
        //倒叙输出 
    }
    cout<<endl;
    return 0;
}