数据结构~基础2~树《二叉树二叉搜索树AVL树B树红黑树》的设计~红黑树
Posted 一乐乐
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构~基础2~树《二叉树二叉搜索树AVL树B树红黑树》的设计~红黑树相关的知识,希望对你有一定的参考价值。
数据结构~基础2~树【《二叉树、二叉搜索树、AVL树、B树、红黑树》的设计】~红黑树
一、 红黑树:
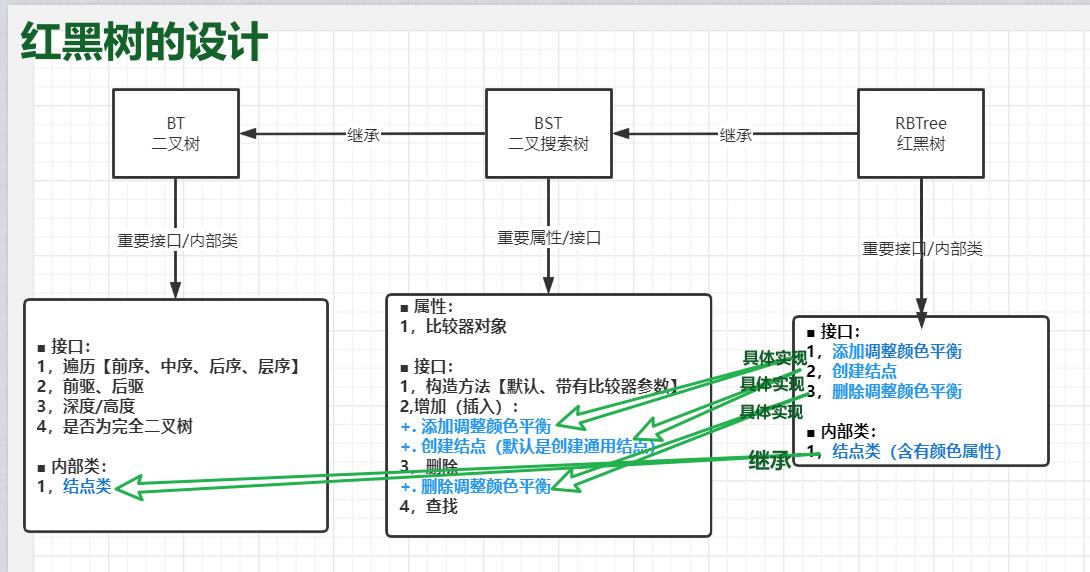
☼ 红黑树之介绍:
-----------形态上是特殊的二叉搜索树【特殊体现在颜色上,同时在逻辑上它是等价于4阶B树的】
❀ 红黑树是怎么等价于4 阶B 树的? ---------红黑树要变成B树:需要将红结点和黑结点进行合并(黑色作为根【也是中间元素】)。
✿ 红黑-->B 树: 结点有四种情况是:①红-黑-红、②红-黑、③黑-红、④黑
❀ 红黑树的通用接口:二叉搜索树的通用接口 + 增加之后、删掉之后、
旋转【左旋、右旋】、旋转之后的处理【更新父结点的关系】(旋转、旋转之后跟AVL 树一样)
■ 插入的所有位置情况:

■ 增加之后:
|
❀ 总结红黑树的添加之后的调整 ❀ : 1,分类:(具体过程需要根据父结点作为左结点、右结点进行对称) (1)不需要调整: ■ 当前结点是根,染黑即可; ■ 父结点是黑,不用处理。 (2)需要调整:(根据叔父结点是否为红色进行划分) ■ case1:叔父是红色,当前结点x 可左可右,染黑 父、叔,染红爷,回溯到结点爷处。 ■ case2:叔父是黑色,当前结点x 是右孩子【红红是LR型】,先进行左旋,转化成case3; (先考虑当前结点是右孩子,因为它处理一下就变成了case3)【小细节,当前结点x 指向 父结点时,旋转x(其实旋转的是原先的父结点的位置)】; ■ case3:叔父是黑色,当前结点x 是左孩子【红红是LL型】,染黑父,染红爷,然后右旋。 |
@Override protected void afterAdd(Node<E> node) { // 判断父结点 Node<E> parent = node.parent; // 添加的是根【当添加第一个结点时】/ 或者上溢到了根结点时 if (parent == null) { black(node); return; } // 若父结点是黑色时,不用处理,直接返回 if (isBlack(parent)) return; // 若叔父结点是红色的[B 树的上溢] Node<E> uncle = parent.sibling(); Node<E> grand = red(parent.parent); if (isRed(uncle)) { // 染黑爸爸、叔叔,把祖父染成红色,相当于新插入的结点 black(uncle); black(parent); // ① 上溢时,也要染红祖父结点 afterAdd(grand); return; } // 观察一下,对代码进行优化,共同拥有的抽到外部之类的 // 来到这里叔父不是红色 if (parent.isLeftChild()) { // L // ② 旋转时,也要 染红结点 if (node.isLeftChild()) { // LL // 染黑父结点,染红祖父结点 black(parent); // 右旋 } else { // LR // 染红自己、染黑祖父结点 black(node); // 左旋后右旋 rotateLeft(parent); } rotateRight(grand); } else { // R // ② 旋转时,也要 染红结点 if (node.isLeftChild()) { // RL // 染红自己、染黑祖父结点 black(node); // 左旋后右旋 rotateRight(parent); } else { // RR // 染黑父结点,染红祖父结点 black(parent); // 左旋 } rotateLeft(grand); } }
■ 删除的所有位置情况:
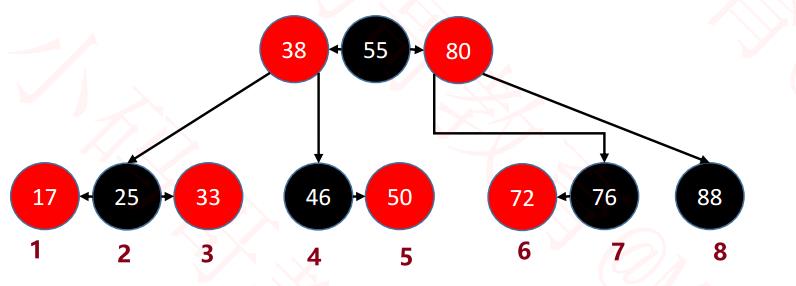
■ 删除之后:
|
❀ 总结红黑树的删除之后的调整 ❀ : 1,删除结点是红色,(完美),不用处理; 2,删除结点是黑色:【看替代结点--前驱/后驱结点】 (1)替代结点是红色,染黑替代结点【前驱/后驱结点】 (2)替代结点是黑色,(若是根,完美,不用处理),黑色结点:
● 黑色叶子结点:【看兄弟】:----- 站在B树角度,发生了下溢 【B树中的处理,找兄弟借,兄弟借不了,找父结点下来合并】 [1] 兄弟是黑色,且能借(至少有一个子红色结点),旋转借出去。 【直接借的话,不符合二叉搜索树的特点,根大于左子树,根小于右子树(需要旋转交换一下结点,(符合二叉搜索树特点)然后再借)】。 [2] 兄弟是黑色,不能借(没有红色结点),看父结点: ① 父结点是红色:染黑父结点,染红兄弟,进行合并。 ② 父结点是黑色,下溢处理。 [3] 兄弟是红色,通过旋转,把侄子(黑色结点)变成兄弟【又变成了删除的结点的兄弟结点是黑色结点】 |
● 黑色叶子结点:【看兄弟】:
[3] 兄弟是红色,通过旋转,把侄子(黑色结点)变成兄弟【又变成了删除的结点的兄弟结点是黑色结点】:
只能是图示:(兄弟跟父结点在同一个B树的子结点上(同一层上),且红色兄弟有两个黑色的子结点)
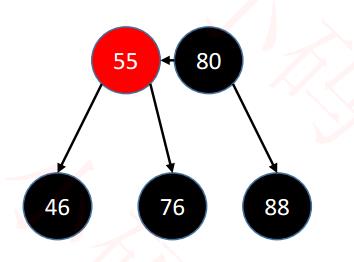
❀ 删除黑色叶子结点时,发生了下溢,而显然不在同一层上的兄弟肯定是不能借出结点,
只能考虑跟自己处于同一层【兄弟的儿子】,向兄弟的儿子进行借。【但是在B树中借的前提,两者是兄弟关系】
所以目标就是要将兄弟的儿子,变成我的兄弟才能顺利成章的借。
[2] 兄弟是黑色,不能借(没有红色结点),看父结点:
① 父结点是红色:染黑父结点,染红兄弟,进行合并。
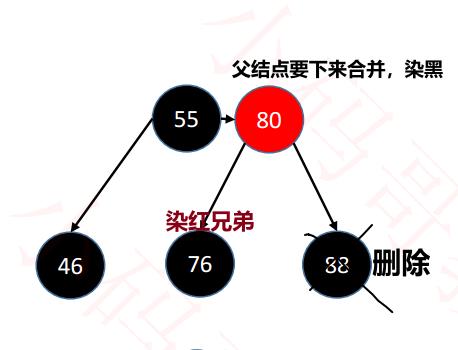
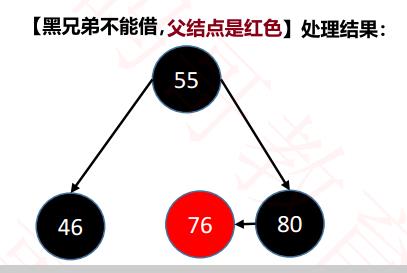
[2] 兄弟是黑色,不能借(没有红色结点),看父结点:
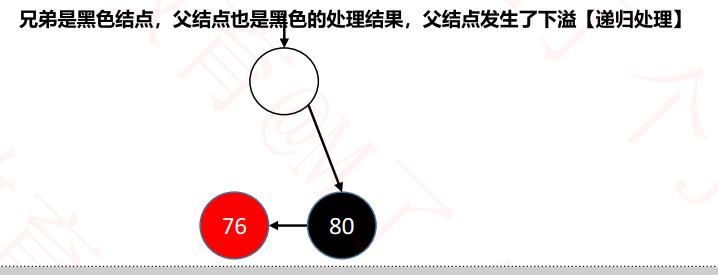
② 父结点是黑色,下溢处理。
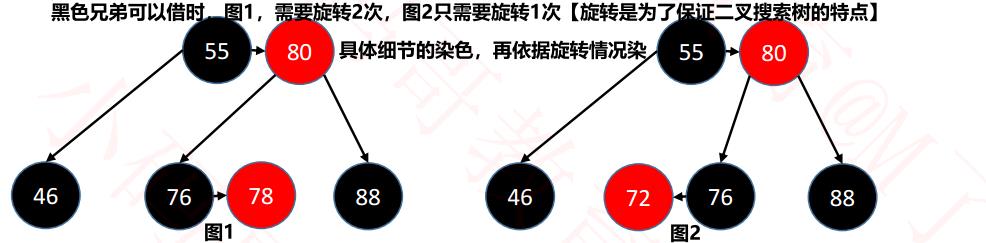
[1] 兄弟是黑色,且能借(至少有一个子红色结点),旋转借出去。【旋转的结果是变成了根(成为独立的B树结点),就需要将其染黑】
【直接借的话,不符合二叉搜索树的特点,根大于左子树,根小于右子树(需要旋转交换一下结点,(符合二叉搜索树特点)然后再借)】。
protected void afterRemove2(Node<E> node, Node<E> replacement) { //删除结点是红色 或者 替代结点【前驱/后驱】是红色 if(isRed(node)) return; if (isRed(replacement)) { black(replacement); return; } //接下来考虑删除结点是黑色【排除掉根的情况】 Node<E> parent = node.parent; // 删除的是根节点 if (parent == null) return; // 删除黑色叶子节点【下溢】 boolean left = parent.left == null || node.isLeftChild();// 判断被删除的node是左还是右 Node<E> sibling = left ? parent.right : parent.left; if (left) { // 被删除的节点在左边,兄弟节点在右边 //看兄弟【兄弟是红色,染黑兄弟,通过左旋,让兄弟成为根,更新一下兄弟位置】 if (isRed(sibling)) { // 兄弟节点是红色 black(sibling); red(parent); rotateLeft(parent); // 重新指一下兄弟(更新一下兄弟位置) sibling = parent.right; } // 【兄弟结点是黑色,兄弟没有红色子结点,不能借】~下溢情况 if (isBlack(sibling.left) && isBlack(sibling.right)) { // 兄弟节点借不出,父节点要向下跟兄弟节点合并【父结点作为下来结点的根】 boolean parentBlack = isBlack(parent); black(parent); red(sibling); if (parentBlack) {//若是父结点原先是黑色,导致塌陷,递归 afterRemove2(parent, null); } // 【兄弟结点是黑色,兄弟有红色子结点可以借】 } else { // 兄弟节点的左结点是黑色,兄弟要先旋转 if (isBlack(sibling.right)) { rotateRight(sibling); //更新一下兄弟结点 sibling = parent.right; } //旋转之后,旋转之后的中心节点继承 parent 的颜色; //旋转之后的左右节点染为 BLACK ----【成为独立的B树结点】 color(sibling, colorOf(parent)); black(sibling.right); black(parent); rotateLeft(parent); } } else { // 被删除的节点在右边,兄弟节点在左边 if (isRed(sibling)) { // 兄弟节点是红色 black(sibling); red(parent); rotateRight(parent); // 更换兄弟 sibling = parent.left; } // 兄弟节点必然是黑色 if (isBlack(sibling.left) && isBlack(sibling.right)) { // 兄弟节点没有1个红色子节点,父节点要向下跟兄弟节点合并 boolean parentBlack = isBlack(parent); black(parent); red(sibling); if (parentBlack) { afterRemove2(parent,null); } } else { // 兄弟节点至少有1个红色子节点,向兄弟节点借元素 // 兄弟节点的左边是黑色,兄弟要先旋转 if (isBlack(sibling.left)) { rotateLeft(sibling); sibling = parent.left; } color(sibling, colorOf(parent)); black(sibling.left); black(parent); rotateRight(parent); } } }
数据结构~基础2~树《二叉树二叉搜索树AVL树B树红黑树》的设计~高度平衡二叉树AVL树
数据结构~基础2~树【《二叉树、二叉搜索树、AVL树、B树、红黑树》的设计】~高度平衡二叉树AVL树
一、 高度平衡二叉树【AVL树】:
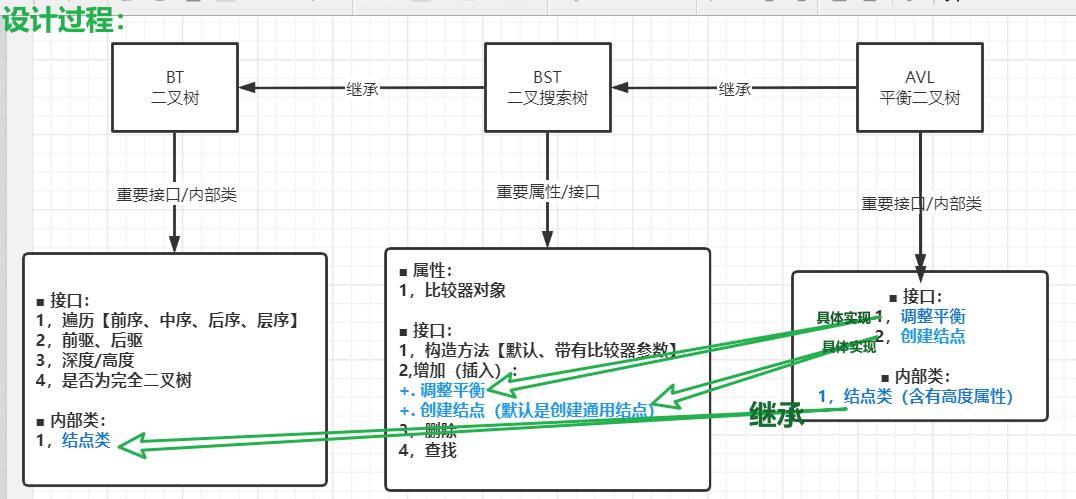
❀ AVL树的通用接口:二叉搜索树的通用接口 + 增加之后、删掉之后、更新高度、
恢复平衡、旋转【左旋、右旋】(更新父结点关系)
■ 增加之后:从当前结点的父结点开始,不断地判断父结点是否平衡,平衡则更新高度,否则则找到第一个失衡的父结点恢复平衡即可。
□ 更新高度:AVL树结点的内定义了一个更新高度的接口方法:
【AVL 树是 从底部向顶部更新高度(底部叶子结点高度是1),每次往上都是取高度更高的子树的高度+1】
□ 恢复平衡【不平衡关系(g-p-n)中 p、n处在与 高度最高的那边,与g同边】:接下来就需要判断是哪一种形态的失衡【LL】【RR】【LR-RR】【RL-LL】
//① 已知g【失衡结点】 情况下,往下调整,先判断p,再判断n,从而得知是【LL】【RR】【LR】【RL】
//② 然后依据相应类型进行旋转。
● 恢复平衡的代码:
// 恢复平衡【不平衡关系(g-p-n)中 p、n处在与 高度最高的那边,与g同边】 private void reBalance(Node<E> grand) { Node<E> parent = ((AVLNode<E>) grand).tallerChild(); // p Node<E> node = ((AVLNode<E>) parent).tallerChild(); // n // 接下来就需要判断是哪一种形态的失衡【LL】【RR】【LR-RR】【RL-LL】 //已知g【失衡结点】 情况下,往下调整,先判断p,再判断n,从而得知是【LL】【RR】【LR】【RL】 if (parent.isLeftChild()) { // 一开始p是L if (node.isLeftChild()) { // LL // //封装成一个方法,右旋接口方法 // // rotateRight(grand); } else { // LR rotateLeft(parent); rotateRight(grand); } } else { // 一开始 p是R if (node.isLeftChild()) { // RL rotateRight(parent); rotateLeft(grand); } else { // RR rotateLeft(grand); } } }
● 旋转【左旋、右旋】的代码:
// 左旋转(RR,右边过重), private void rotateLeft(Node<E> grand) { //左旋,则p必然是g的右孩子 Node<E> parent = grand.right; Node<E> child = parent.left; //RR,右边过重,左旋 grand.right = child; parent.left = grand; // 旋转之后更新 afterRotate(grand, parent, child); } // 右旋转(LL,左边过重) private void rotateRight(Node<E> grand) { //右旋,p必然是g的左孩子 Node<E> parent = grand.left; Node<E> child = parent.right; // LL,左边过重,右旋 grand.left = child; parent.right = grand; // 旋转之后更新 afterRotate(grand, parent, child); }
● 旋转之后【结点关系】和【父结点高度】的更新代码:
//旋转之后父节点关系的更新【首先先更新 p、然后是child、 grand】与父结点高度的更新 private void afterRotate(Node<E> grand, Node<E> parent, Node<E> child) { parent.parent = grand.parent; if (grand.isLeftChild()) { grand.parent.left = parent; } else if (grand.isRightChild()) { grand.parent.right = parent; } else { root = parent; } // 更新child的父结点 if (child != null) { child.parent = grand; } // 更新grand的父节点 grand.parent = parent; // 更新作为父结点的高度[从低到高,先更新 g、再更新 p] updateHeight(grand); updateHeight(parent); }
■ 删除之后:与增加之后同理【只是增加之后仅需修复第一个失衡的父结点,而删除之后是不断地修改失衡父结点】
以上是关于数据结构~基础2~树《二叉树二叉搜索树AVL树B树红黑树》的设计~红黑树的主要内容,如果未能解决你的问题,请参考以下文章