56.图的广度优先和深度优先

Posted 2021-10-29 upupup-999

 

 

 

 

 

 

 

 

 

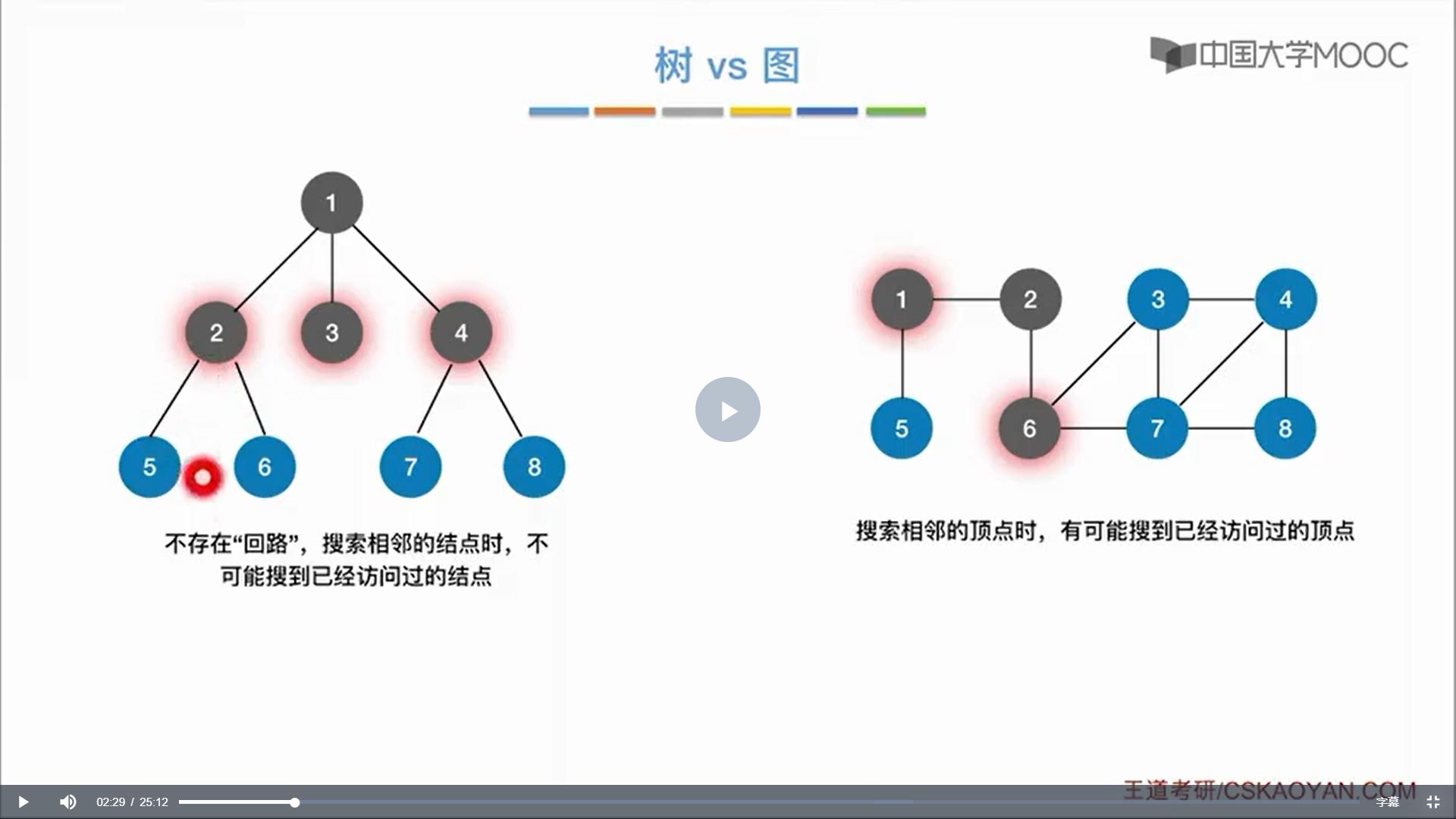
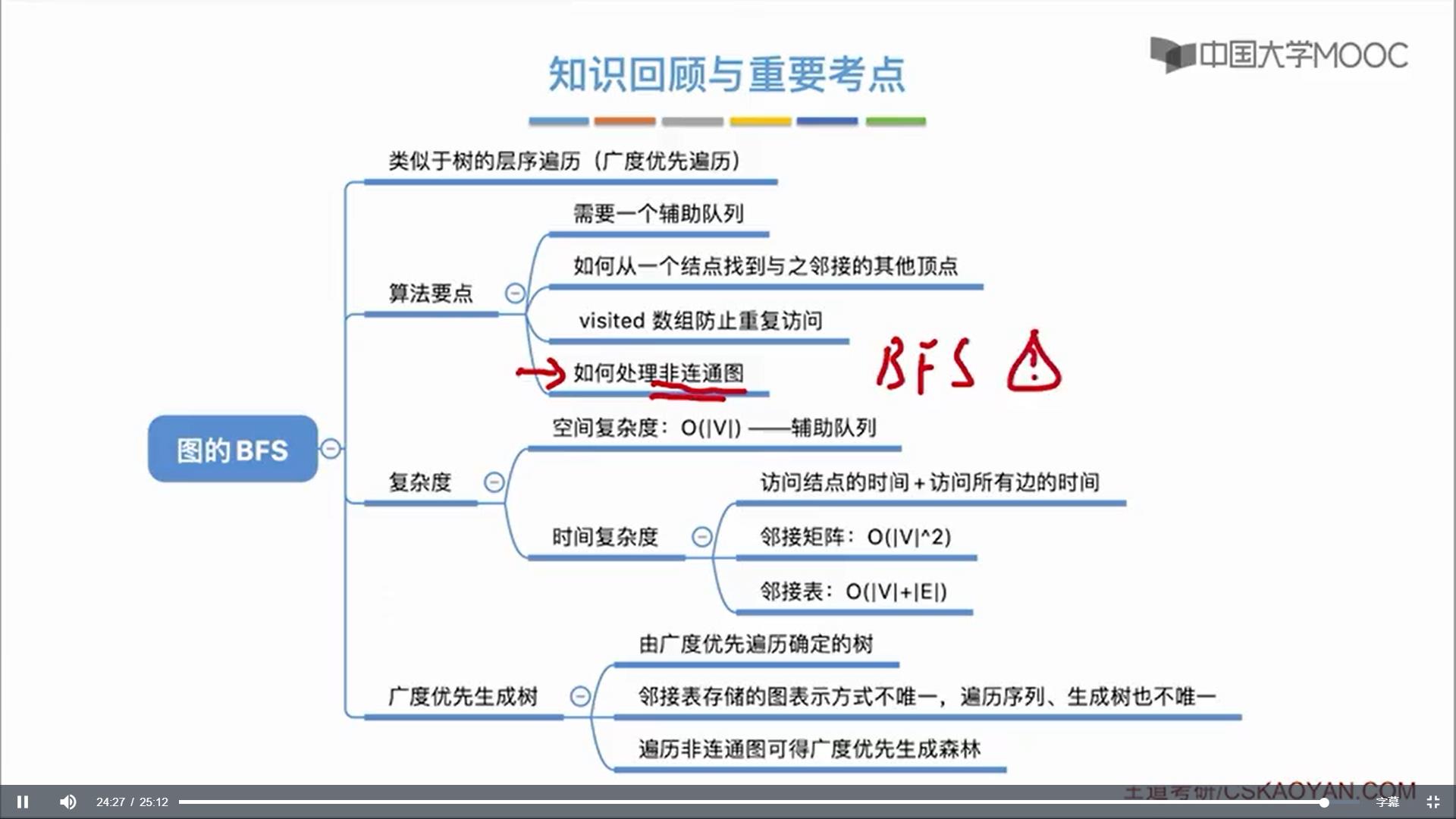
图的遍历（深度优先和广度优先）

图的遍历

定义

遍历（Traversing Graph）：从图中某点出发访问各顶点，每个顶点仅被访问一次（有且仅有一次）。
深度优先遍历（Depth First Search）：也称深度优先搜索，简称DFS。从图中某个顶点v出发做深度优先搜索，访问顶点v，然后从v的未被访问的邻接顶点出发做深度优先搜索，直到图中所有和v有路径相通的顶点都被访问到。明显，这是个递归的过程。
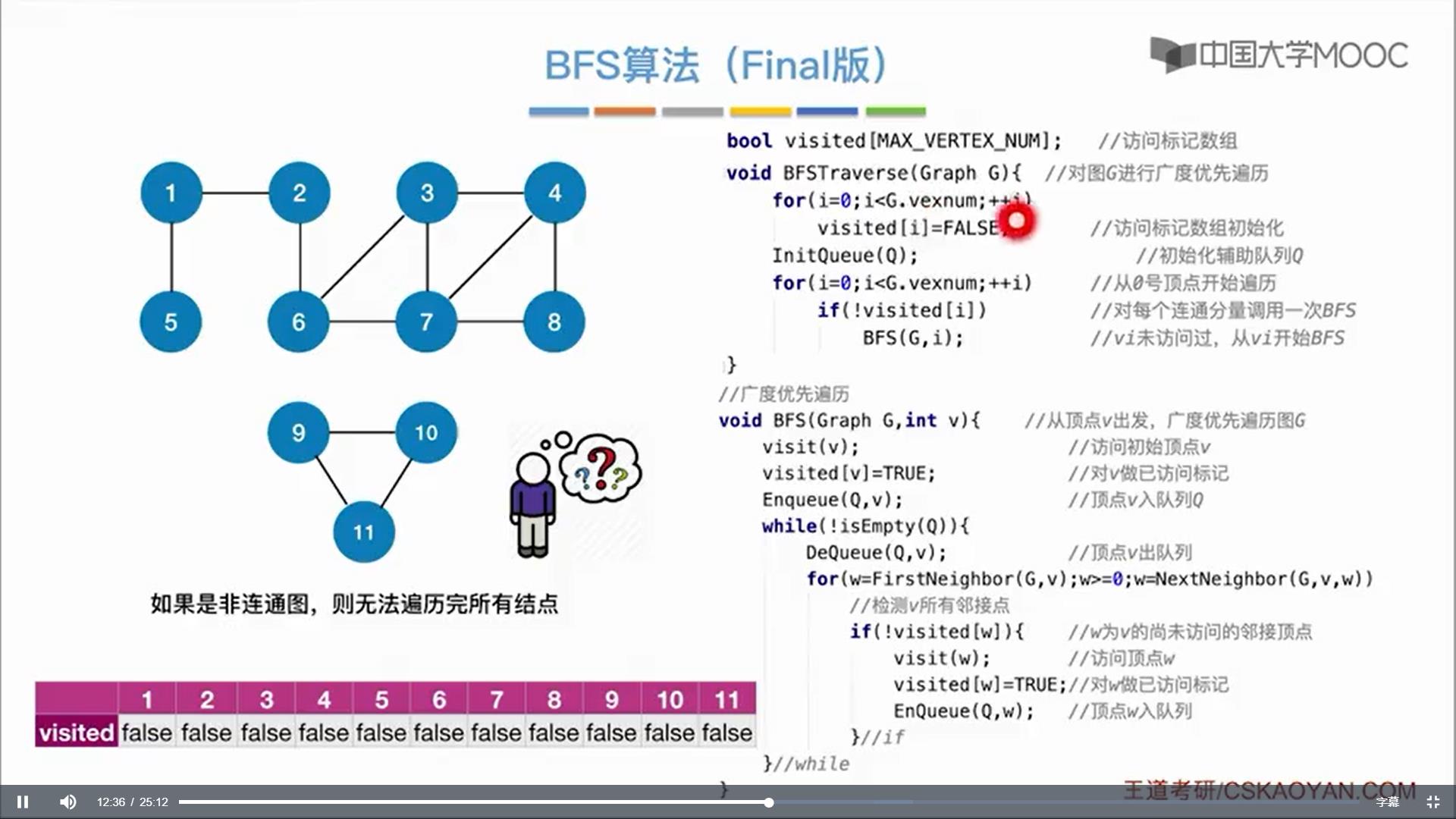
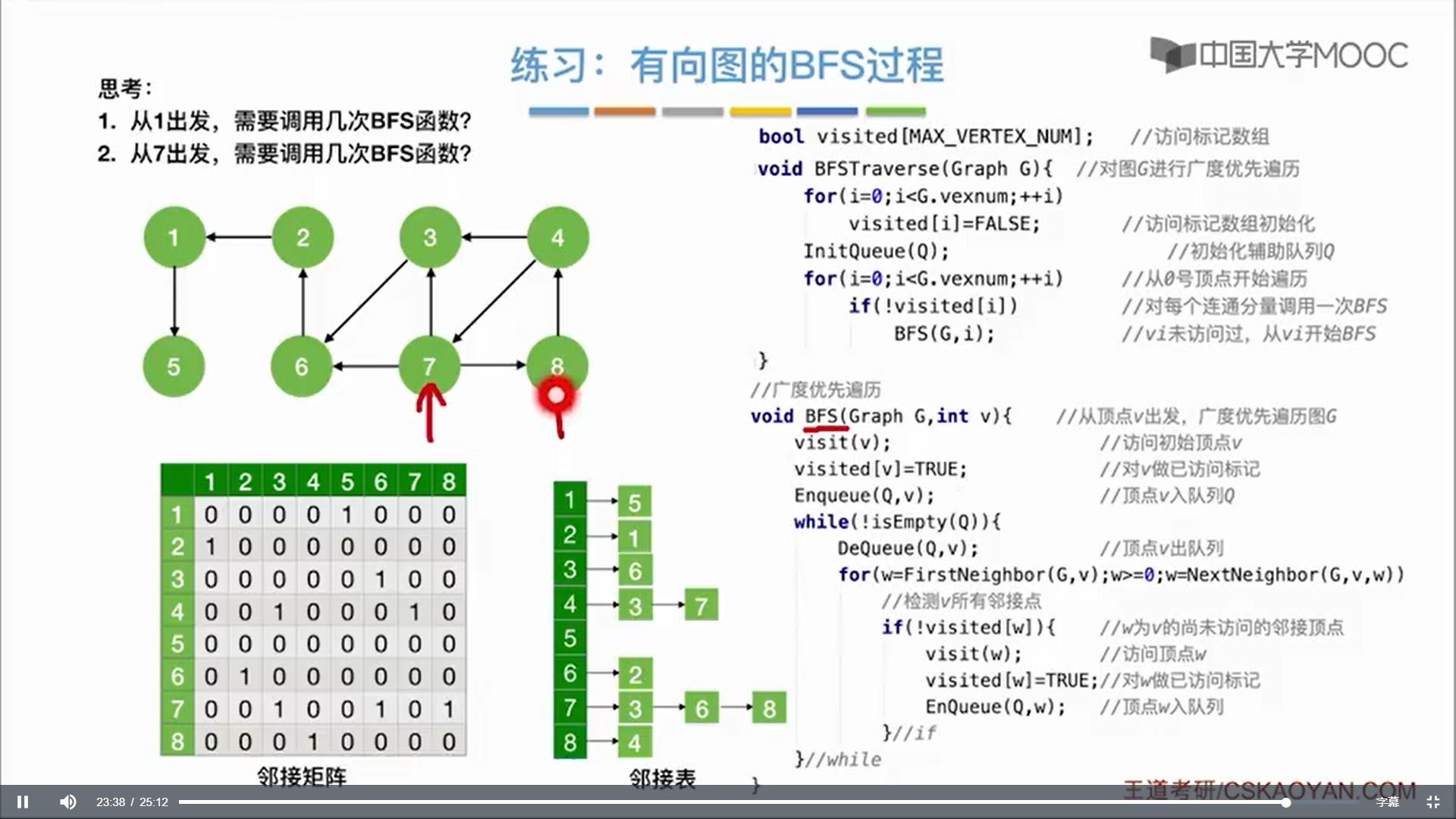
广度优先遍历（Breadth First Search）：也称广度优先搜索，简称BFS。从图中某个顶点v出发做广度优先搜索，先缓存顶点v，从缓存中取出顶点v并访问，然后缓存v的未被访问的邻接顶点（可理解为v的下层顶点），从缓存中取出顶点，再访问，直到图中所有和v有路径相通的顶点都被访问到。

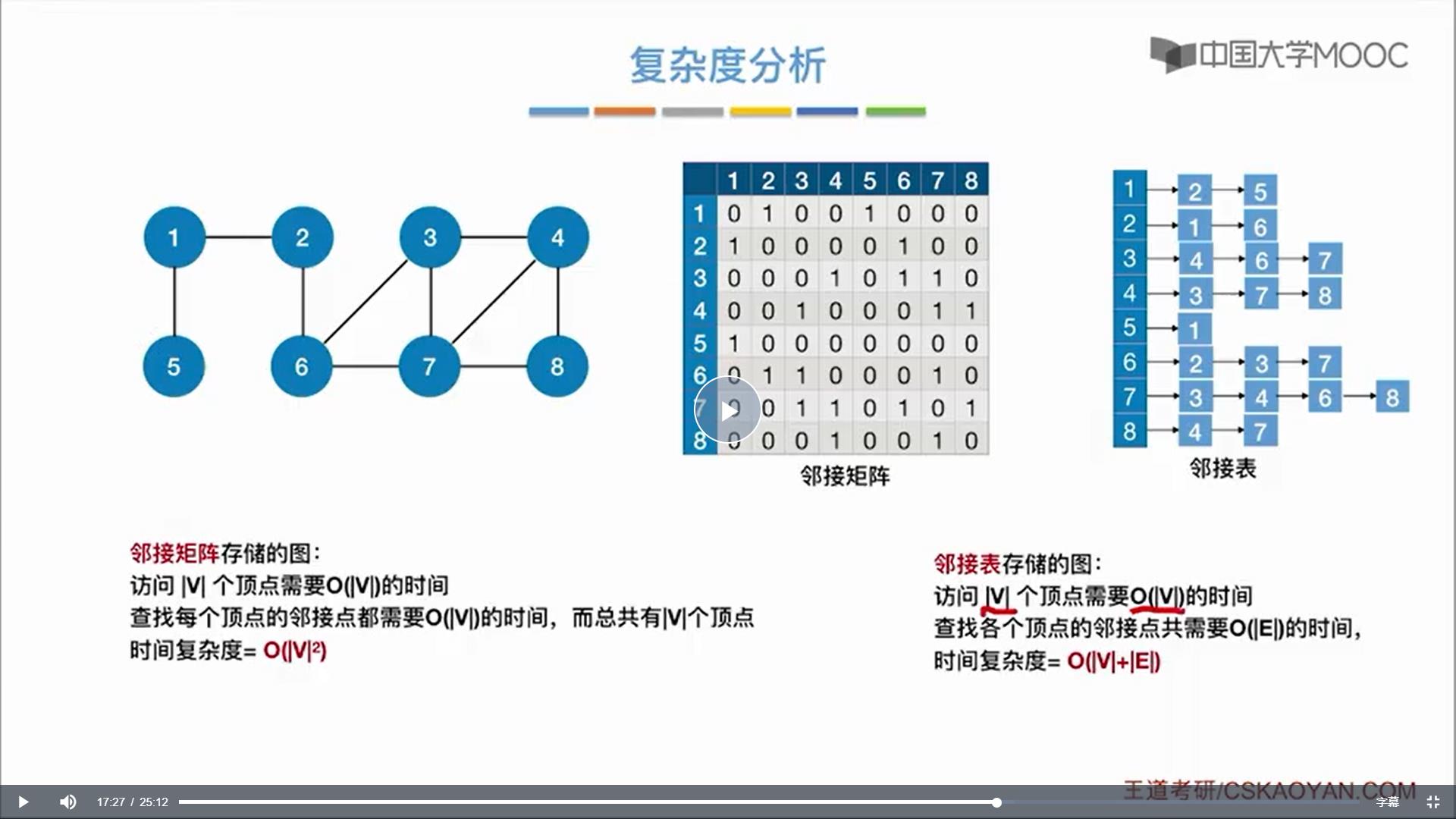
复杂度分析

从下面的代码可以得出，对于n个顶点e条边的图来说，邻接矩阵表示的图由于是二维数组，所以遍历二维数组需要O(n²)的时间；对于邻接表表示的图，找邻接点所需的时间取决于顶点和边的数量，所以遍历邻接表表示的图的时间复杂度是O(n+e)的时间。

代码

以下图中的图为例，采用不同的遍历方式遍历不同存储结构的图。

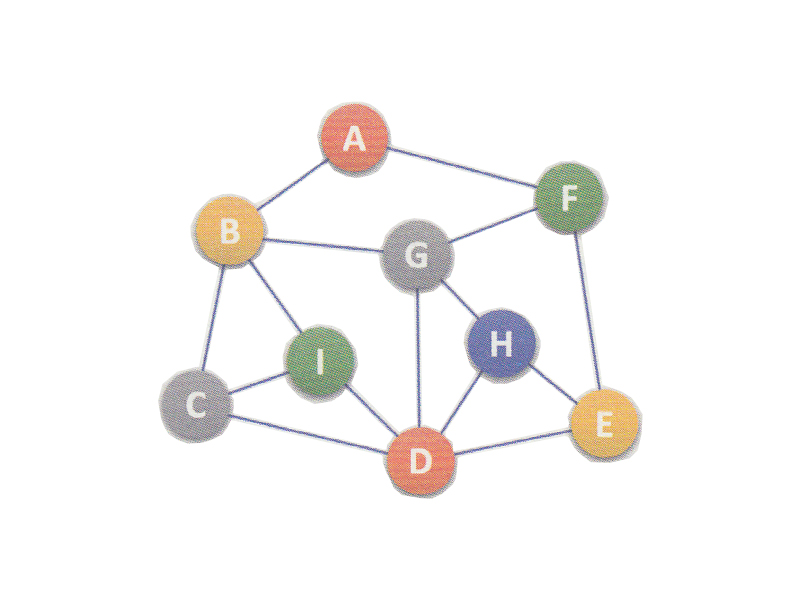
C#代码

using System;
using System.Collections.Generic;

namespace GraphDfs
{
    class Program
    {
        static void Main(string[] args)
        {
            // 创建图（邻接矩阵表示法）
            int self = GraphAjacencyMatrix.SelfToSelf,
                noedge = GraphAjacencyMatrix.NoEdge;

            AjacentVertex[] vertexes = new AjacentVertex[] {
                new AjacentVertex(){ Data = "A" },  // 0
                new AjacentVertex(){ Data = "B" },  // 1
                new AjacentVertex(){ Data = "C" },  // 2
                new AjacentVertex(){ Data = "D" },  // 3
                new AjacentVertex(){ Data = "E" },  // 4
                new AjacentVertex(){ Data = "F" },  // 5
                new AjacentVertex(){ Data = "G" },  // 6
                new AjacentVertex(){ Data = "H" },  // 7
                new AjacentVertex(){ Data = "I" },  // 8
            };

            int[][] edges = new int[][] {
                new int[]{ self, 1, noedge, noedge, noedge, 1, noedge, noedge, noedge },  // A
                new int[]{ 1, self, 1, noedge, noedge, noedge, 1, noedge, 1 },  // B
                new int[]{ noedge, 1, self, 1, noedge, noedge, noedge, noedge, 1 },  // C
                new int[]{ noedge, noedge, 1, self, 1, noedge, 1, 1, 1 },  // D
                new int[]{ noedge, noedge, noedge, 1, self, 1, noedge, 1, noedge },  // E
                new int[]{ 1, noedge, noedge, noedge, 1, self, 1, noedge, noedge },  // F
                new int[]{ noedge, 1, noedge, 1, noedge, 1, self, 1, noedge },  // G
                new int[]{ noedge, noedge, noedge, 1, 1, noedge, 1, self, noedge },  // H
                new int[]{ noedge, 1, 1, 1, noedge, noedge, noedge, noedge, self },  // I
            };

            GraphAjacencyMatrix graph = new GraphAjacencyMatrix(vertexes, edges);

            // 创建图（邻接表表示法）
            Vertex[] vertexesAjacencyList = new Vertex[] {
                new Vertex("A", new Edge[]{ new Edge(1, "<A, B>"), new Edge(5, "<A, F>") }),  // 0
                new Vertex("B", new Edge[]{ new Edge(0, "<B, A>"), new Edge(2, "<B, C>"), new Edge(6, "<B, G>"), new Edge(8, "<B, I>")}),  // 1
                new Vertex("C", new Edge[]{ new Edge(1, "<C, B>"), new Edge(3, "<C, D>"), new Edge(8, "<C, I>")}),  // 2
                new Vertex("D", new Edge[]{ new Edge(2, "<D, C>"), new Edge(4, "<D, E>"), new Edge(6, "<D, G>"), new Edge(7, "<D, H>"), new Edge(8, "<D, I>")}),  // 3
                new Vertex("E", new Edge[]{ new Edge(3, "<E, D>"), new Edge(5, "<E, F>"), new Edge(7, "<E, H>")}),  // 4
                new Vertex("F", new Edge[]{ new Edge(0, "<F, A>"), new Edge(4, "<F, E>"), new Edge(6, "<F, G>")}),  // 5
                new Vertex("G", new Edge[]{ new Edge(1, "<G, B>"), new Edge(3, "<G, D>"), new Edge(5, "<G, F>"), new Edge(7, "<G, H>")}),  // 6
                new Vertex("H", new Edge[]{ new Edge(3, "<H, D>"), new Edge(4, "<H, E>"), new Edge(6, "<H, G>"),}),  // 7
                new Vertex("I", new Edge[]{ new Edge(1, "<I, B>"), new Edge(2, "<I, C>"), new Edge(3, "<I, D>"),}),  // 8
            };

            GraphAjacencyList graphAjacencyList = new GraphAjacencyList(vertexesAjacencyList);

            Console.WriteLine("图的深度优先搜索（邻接矩阵表示法）：");
            Dfs1(graph);
            /**
             运行结果：
            图的深度优先搜索（邻接矩阵表示法）：
            V0 = A
            V1 = B
            V2 = C
            V3 = D
            V4 = E
            V7 = H
            V6 = G
            V8 = I
            V5 = F
             */

            Console.WriteLine("图的深度优先搜索（邻接表表示法）：");
            Dfs2(graphAjacencyList);
            /**
             运行结果：
            图的深度优先搜索（邻接表表示法）：
            V0 = A
            V1 = B
            V2 = C
            V3 = D
            V4 = E
            V7 = H
            V6 = G
            V8 = I
            V5 = F
             */

            Console.WriteLine("图的广度优先搜索（邻接矩阵表示法）：");
            Bfs1(graph);
            /**
             运行结果：
            图的广度优先搜索（邻接矩阵表示法）：
            V0 = A
            V1 = B
            V5 = F
            V2 = C
            V6 = G
            V8 = I
            V4 = E
            V3 = D
            V7 = H
             */

            Console.WriteLine("图的广度优先搜索（邻接表表示法）：");
            Bfs2(graphAjacencyList);
            /**
             运行结果：
            图的广度优先搜索（邻接表表示法）：
            V0 = A
            V5 = F
            V1 = B
            V6 = G
            V4 = E
            V8 = I
            V2 = C
            V7 = H
            V3 = D
             */
        }

        /// <summary>
        /// 图的深度优先搜索（Depth-First-Search）算法（非递归）。
        /// 图用邻接矩阵表示。
        /// </summary>
        /// <param name="g">用邻接矩阵表示的图。</param>
        public static void Dfs1(GraphAjacencyMatrix g)
        {
            bool[] isDiscovered = new bool[g.NumberOfVertex];

            for (int i = 0; i < isDiscovered.Length; i++)
            {
                isDiscovered[i] = false;
            }

            Stack<int> s = new Stack<int>();

            for (int i = 0; i < g.NumberOfVertex; i++)
            {
                if (isDiscovered[i] == false)
                {
                    s.Push(i);
                    isDiscovered[i] = true;
                }

                while (s.Count != 0)
                {
                    int v = s.Pop();

                    // visit node operation
                    Console.WriteLine($"V{v} = {g.Vertexes[v].Data}");

                    for (int j = g.NumberOfVertex - 1; j >= 0; j--)
                    //for (int j = 0; j < g.NumberOfVertex; j++)
                    {
                        if (g.Edges[v][j] != GraphAjacencyMatrix.SelfToSelf &&
                            g.Edges[v][j] != GraphAjacencyMatrix.NoEdge &&
                            isDiscovered[j] == false)
                        {
                            s.Push(j);
                            isDiscovered[j] = true;
                        }
                    }
                }
            }
        }
        /// <summary>
        /// 图的深度优先搜索（Depth-First-Search）算法（非递归）。
        /// 图用邻接表表示。
        /// </summary>
        /// <param name="g">用邻接矩阵表示的图。</param>
        public static void Dfs2(GraphAjacencyList g)
        {
            bool[] isDiscovered = new bool[g.NumberOfVertex];

            for (int i = 0; i < isDiscovered.Length; i++)
            {
                isDiscovered[i] = false;
            }

            Stack<int> s = new Stack<int>();

            for (int i = 0; i < g.NumberOfVertex; i++)
            {
                if (isDiscovered[i] == false)
                {
                    s.Push(i);
                    isDiscovered[i] = true;
                }

                while (s.Count != 0)
                {
                    int v = s.Pop();

                    // visit node operation
                    Console.WriteLine($"V{v} = {g.Vertexes[v].Data}");

                    Edge e = g.Vertexes[v].Edge;

                    while (e != null)
                    {
                        int j = e.HeadVertex;

                        if (isDiscovered[j] == false)
                        {
                            s.Push(j);
                            isDiscovered[j] = true;
                        }
                        e = e.Next;
                    }
                }
            }
        }
        /// <summary>
        /// 图的广度优先搜索（Depth-First-Search）算法。
        /// 图用邻接矩阵表示。
        /// </summary>
        /// <param name="g">用邻接矩阵表示的图。</param>
        public static void Bfs1(GraphAjacencyMatrix g)
        {
            bool[] isDiscovered = new bool[g.NumberOfVertex];

            for (int i = 0; i < isDiscovered.Length; i++)
            {
                isDiscovered[i] = false;
            }

            Queue<int> q = new Queue<int>();

            for (int i = 0; i < g.NumberOfVertex; i++)
            {
                if (isDiscovered[i] == false)
                {
                    q.Enqueue(i);
                    isDiscovered[i] = true;
                }

                while (q.Count != 0)
                {
                    int v = q.Dequeue();

                    // visit node operation
                    Console.WriteLine($"V{v} = {g.Vertexes[v].Data}");

                    for (int j = 0; j < g.NumberOfVertex; j++)
                    {
                        if (g.Edges[v][j] != GraphAjacencyMatrix.SelfToSelf &&
                            g.Edges[v][j] != GraphAjacencyMatrix.NoEdge &&
                            isDiscovered[j] == false)
                        {
                            q.Enqueue(j);
                            isDiscovered[j] = true;
                        }
                    }
                }
            }
        }

        /// <summary>
        /// 图的广度优先搜索（Breadth-First-Search）算法。
        /// 图用邻接表表示。
        /// </summary>
        /// <param name="g">用邻接矩阵表示的图。</param>
        public static void Bfs2(GraphAjacencyList g)
        {
            bool[] isDiscovered = new bool[g.NumberOfVertex];

            for (int i = 0; i < isDiscovered.Length; i++)
            {
                isDiscovered[i] = false;
            }

            Queue<int> q = new Queue<int>();

            for (int i = 0; i < g.NumberOfVertex; i++)
            {
                if (isDiscovered[i] == false)
                {
                    q.Enqueue(i);
                    isDiscovered[i] = true;
                }

                while (q.Count != 0)
                {
                    int v = q.Dequeue();
                    // visit node operation
                    Console.WriteLine($"V{v} = {g.Vertexes[v].Data}");

                    Edge e = g.Vertexes[v].Edge;
                    while (e != null)
                    {
                        int j = e.HeadVertex;
                        if (isDiscovered[j] == false)
                        {
                            q.Enqueue(j);
                            isDiscovered[j] = true;
                        }
                        e = e.Next;
                    }
                }
            }
        }
    }

    /// <summary>
    /// 用邻接矩阵表示的图的顶点类。
    /// </summary>
    public class AjacentVertex
    {
        /// <summary>
        /// 顶点的数据域。
        /// </summary>
        public string Data { get; set; } = "";
    }

    /// <summary>
    /// 邻接矩阵表示的图类。
    /// </summary>
    public class GraphAjacencyMatrix
    {
        /// <summary>
        /// 用系统能够表示的最大整数表示无穷。
        /// </summary>
        public static int Inifinity = int.MaxValue;
        /// <summary>
        /// 用无穷表示不存在边(Vi, Vj)或弧<Vi, Vj>
        /// </summary>
        public static int NoEdge = Inifinity;
        /// <summary>
        /// 用于在邻接矩阵中表示顶点Vi到顶点Vi的情形。
        /// </summary>
        public static int SelfToSelf = 0;
        /// <summary>
        /// 图中的所有顶点构成的顶点数组。
        /// </summary>
        public AjacentVertex[] Vertexes { get; private set; }
        /// <summary>
        /// 图中的所有边。用一个二维整型数组表示。
        /// 例如：Edges[1][2] == 2表示Vertexes数组中
        /// 索引为1的顶点到索引为2的顶点<V1, V2>弧的权值为2。
        /// </summary>
        public int[][] Edges { get; private set; }
        /// <summary>
        /// 图的顶点数量。
        /// </summary>
        public int NumberOfVertex { get => Vertexes.Length; }
        /// <summary>
        /// 提供图的所有顶点及边，用于创建图类实例。
        /// </summary>
        /// <param name="vertexes">图中的所有顶点。</param>
        /// <param name="edges">图中的所有边。</param>
        public GraphAjacencyMatrix(AjacentVertex[] vertexes, int[][] edges)
        {
            Vertexes = vertexes;
            Edges = edges;
        }
    }

    /// <summary>
    /// 图G的顶点。用邻接表来表示顶点的出边。
    /// </summary>
    public class Vertex
    {
        /// <summary>
        /// 存储的数据。
        /// </summary>
        public string Data { get; set; } = "";
        /// <summary>
        /// 出边。
        /// </summary>
        public Edge Edge { get; set; } = null;

        public Vertex(string data, Edge[] adjacentEdges)
        {
            this.Data = data;

            Edge e = null;

            for (int i = 0; i < adjacentEdges.Length; i++)
            {
                e = new Edge(adjacentEdges[i].HeadVertex, adjacentEdges[i].Data);
                e.Next = (Edge == null ? null : Edge);
                Edge = e;
            }
        }
    }

    /// <summary>
    /// 图G的边。以邻接表表示顶点的出边。
    /// </summary>
    public class Edge
    {
        /// <summary>
        /// 边的弧头顶点在顶点数组中的索引。
        /// </summary>
        public int HeadVertex { get; set; } = -1;
        /// <summary>
        /// 边的弧尾顶点的下一条出边。
        /// </summary>
        public Edge Next { get; set; } = null;
        /// <summary>
        /// 边的描述/数据。
        /// </summary>
        public string Data { get; set; } = string.Empty;

        public Edge(int vertex = -1, string data = "", Edge edge = null)
        {
            this.HeadVertex = vertex;
            this.Next = edge;
            this.Data = data;
        }
    }

    /// <summary>
    /// 邻接表表示的图类。
    /// </summary>
    public class GraphAjacencyList
    {
        /// <summary>
        /// 图中的所有顶点构成的顶点数组。
        /// </summary>
        public Vertex[] Vertexes { get; private set; }
        /// <summary>
        /// 图的顶点数量。
        /// </summary>
        public int NumberOfVertex { get => Vertexes.Length; }
        /// <summary>
        /// 提供图的所有顶点及边，用于创建图类实例。
        /// </summary>
        /// <param name="vertexes">图中的所有顶点。</param>
        public GraphAjacencyList(Vertex[] vertexes)
        {
            Vertexes = vertexes;
        }
    }

}

TypeScript代码

/**
 * 用邻接矩阵表示的图的顶点类。
 */
class AjacentVertex {
    /**
     * 顶点的数据域。
    */
    data: string = "";
}

/**
 * 邻接矩阵表示的图类。
 */
class GraphAjacencyMatrix {
    /**
     * 用系统能够表示的最大整数表示无穷。
     */
    static inifinity: number = Number.MAX_VALUE;

    /**
     * 用无穷表示不存在边(Vi, Vj)或弧<Vi, Vj>
     */
    static noEdge: number = GraphAjacencyMatrix.inifinity;

    /**
     * 用于在邻接矩阵中表示顶点Vi到顶点Vi的情形。
     */
    static selfToSelf: number = 0;

    /**
     * 图中的所有顶点构成的顶点数组。
     */
    vertexes: AjacentVertex[];

    /**
     * 图中的所有边。用一个二维整型数组表示。
     * 例如：Edges[1][2] == 2表示Vertexes数组中
     * 索引为1的顶点到索引为2的顶点<V1, V2>弧的权值为2。
     */
    edges: number[][];

    /**
     * 图的顶点数量。
     */
    get numberOfVertex(): number {
        return this.vertexes.length;
    }

    /**
     * 提供图的所有顶点及边，用于创建图类实例。
     * @param vertexes 图中的所有顶点。
     * @param edges 图中的所有边。
     */
    constructor(vertexes: AjacentVertex[], edges: number[][]) {
        this.vertexes = vertexes;
        this.edges = edges;
    }
}

/**
 * 图G的顶点。用邻接表来表示顶点的出边。
 */
class Vertex {

    /**
     * 存储的数据。
     */
    data: string = "";

    /**
     * 出边。
     */
    edge: Edge = null;

    constructor(data: string, adjacentEdges: Edge[]) {

        this.data = data;

        let e: Edge = null;

        for (let i: number = 0; i < adjacentEdges.length; i++) {
            e = new Edge(adjacentEdges[i].headVertex, adjacentEdges[i].data);
            e.next = (this.edge == null ? null : this.edge);
            this.edge = e;
        }
    }
}

/**
 * 图G的边。以邻接表表示顶点的出边。
 */
class Edge {

    /**
     * 边的弧头顶点在顶点数组中的索引。
     */
    headVertex: number = -1;

    /**
     * 边的弧尾顶点的下一条出边。
     */
    next: Edge = null;

    /**
     * 边的描述/数据。
     */
    data: string = "";

    constructor(vertex: number = -1, data: string = "", edge: Edge = null) {
        this.headVertex = vertex;
        this.next = edge;
        this.data = data;
    }
}

/**
 * 邻接表表示的图类。
 */
class GraphAjacencyList {

    /**
     * 图中的所有顶点构成的顶点数组。
     */
    vertexes: Vertex[];

    /**
     * 图的顶点数量。
     */
    get numberOfVertex(): number {
        return this.vertexes.length;
    }

    /**
     * 提供图的所有顶点及边，用于创建图类实例。
     * @param vertexes 图中的所有顶点。
     */
    constructor(vertexes: Vertex[]) {
        this.vertexes = vertexes;
    }
}

/**
 * 图的深度优先搜索（Depth-First-Search）算法（非递归）。
 * 图用邻接矩阵表示。
 * @param g 用邻接矩阵表示的图。
 */
function dfs1(g: GraphAjacencyMatrix): void {
    let isDiscovered: boolean[] = [];

    isDiscovered.length = g.numberOfVertex;

    for (let i: number = 0; i < isDiscovered.length; i++) {
        isDiscovered[i] = false;
    }

    let s: number[] = [];

    for (let i: number = 0; i < g.numberOfVertex; i++) {
        if (isDiscovered[i] == false) {
            s.push(i);
            isDiscovered[i] = true;
        }

        while (s.length != 0) {
            let v: number = s.pop();

            // visit node operation
            console.log(`V${v} = ${g.vertexes[v].data}`);

            for (let j: number = g.numberOfVertex - 1; j >= 0; j--)
            //for (int j = 0; j < g.NumberOfVertex; j++)
            {
                if (g.edges[v][j] != GraphAjacencyMatrix.selfToSelf &&
                    g.edges[v][j] != GraphAjacencyMatrix.noEdge &&
                    isDiscovered[j] == false) {
                    s.push(j);
                    isDiscovered[j] = true;
                }
            }
        }
    }
}

/**
 * 图的深度优先搜索（Depth-First-Search）算法（非递归）。
 * 图用邻接表表示。
 * @param g 用邻接矩阵表示的图。
 */
function dfs2(g: GraphAjacencyList): void {
    let isDiscovered: boolean[] = [];

    isDiscovered.length = g.numberOfVertex;

    for (let i: number = 0; i < isDiscovered.length; i++) {
        isDiscovered[i] = false;
    }

    let s: number[] = [];

    for (let i: number = 0; i < g.numberOfVertex; i++) {
        if (isDiscovered[i] == false) {
            s.push(i);
            isDiscovered[i] = true;
        }

        while (s.length != 0) {
            let v: number = s.pop();

            // visit node operation
            console.log(`V${v} = ${g.vertexes[v].data}`);

            let e: Edge = g.vertexes[v].edge;

            while (e != null) {
                let j: number = e.headVertex;

                if (isDiscovered[j] == false) {
                    s.push(j);
                    isDiscovered[j] = true;
                }
                e = e.next;
            }
        }
    }
}

/**
 * 图的广度优先搜索（Depth-First-Search）算法。
 * 图用邻接矩阵表示。
 * @param g 用邻接矩阵表示的图。
 */
function bfs1(g: GraphAjacencyMatrix): void {
    let isDiscovered: boolean[] = [];

    isDiscovered.length = g.numberOfVertex;

    for (let i: number = 0; i < isDiscovered.length; i++) {
        isDiscovered[i] = false;
    }

    let q: number[] = [];

    for (let i: number = 0; i < g.numberOfVertex; i++) {
        if (isDiscovered[i] == false) {
            q.push(i);
            isDiscovered[i] = true;
        }

        while (q.length != 0) {
            let v: number = q.shift();

            // visit node operation
            console.log(`V${v} = ${g.vertexes[v].data}`);

            for (let j: number = 0; j < g.numberOfVertex; j++) {
                if (g.edges[v][j] != GraphAjacencyMatrix.selfToSelf &&
                    g.edges[v][j] != GraphAjacencyMatrix.noEdge &&
                    isDiscovered[j] == false) {
                    q.push(j);
                    isDiscovered[j] = true;
                }
            }
        }
    }
}

/**
 * 图的广度优先搜索（Breadth-First-Search）算法。
 * 图用邻接表表示。
 * @param g 用邻接矩阵表示的图。
 */
function bfs2(g: GraphAjacencyList): void {
    let isDiscovered: boolean[] = [];

    isDiscovered.length = g.numberOfVertex;

    for (let i: number = 0; i < isDiscovered.length; i++) {
        isDiscovered[i] = false;
    }

    let q: number[] = [];

    for (let i: number = 0; i < g.numberOfVertex; i++) {
        if (isDiscovered[i] == false) {
            q.push(i);
            isDiscovered[i] = true;
        }

        while (q.length != 0) {
            let v: number = q.shift();

            // visit node operation
            console.log(`V${v} = ${g.vertexes[v].data}`);

            let e: Edge = g.vertexes[v].edge;
            while (e != null) {
                let j: number = e.headVertex;
                if (isDiscovered[j] == false) {
                    q.push(j);
                    isDiscovered[j] = true;
                }
                e = e.next;
            }
        }
    }
}

function main(): void {
    // 创建图（邻接矩阵表示法）
    let self: number = GraphAjacencyMatrix.selfToSelf,
        noedge = GraphAjacencyMatrix.noEdge;

    let vertexes: AjacentVertex[] = [
        { data: "A" },  // 0
        { data: "B" },  // 1
        { data: "C" },  // 2
        { data: "D" },  // 3
        { data: "E" },  // 4
        { data: "F" },  // 5
        { data: "G" },  // 6
        { data: "H" },  // 7
        { data: "I" },  // 8
    ];

    let edges: number[][] = [
        [self, 1, noedge, noedge, noedge, 1, noedge, noedge, noedge],  // A
        [1, self, 1, noedge, noedge, noedge, 1, noedge, 1],  // B
        [noedge, 1, self, 1, noedge, noedge, noedge, noedge, 1],  // C
        [noedge, noedge, 1, self, 1, noedge, 1, 1, 1],  // D
        [noedge, noedge, noedge, 1, self, 1, noedge, 1, noedge],  // E
        [1, noedge, noedge, noedge, 1, self, 1, noedge, noedge],  // F
        [noedge, 1, noedge, 1, noedge, 1, self, 1, noedge],  // G
        [noedge, noedge, noedge, 1, 1, noedge, 1, self, noedge],  // H
        [noedge, 1, 1, 1, noedge, noedge, noedge, noedge, self],  // I
    ];

    let graph: GraphAjacencyMatrix = new GraphAjacencyMatrix(vertexes, edges);

    // 创建图（邻接表表示法）
    let vertexesAjacencyList: Vertex[] = [
        new Vertex("A", [new Edge(1, "<A, B>"), new Edge(5, "<A, F>")]),  // 0
        new Vertex("B", [new Edge(0, "<B, A>"), new Edge(2, "<B, C>"), new Edge(6, "<B, G>"), new Edge(8, "<B, I>")]),  // 1
        new Vertex("C", [new Edge(1, "<C, B>"), new Edge(3, "<C, D>"), new Edge(8, "<C, I>")]),  // 2
        new Vertex("D", [new Edge(2, "<D, C>"), new Edge(4, "<D, E>"), new Edge(6, "<D, G>"), new Edge(7, "<D, H>"), new Edge(8, "<D, I>")]),  // 3
        new Vertex("E", [new Edge(3, "<E, D>"), new Edge(5, "<E, F>"), new Edge(7, "<E, H>")]),  // 4
        new Vertex("F", [new Edge(0, "<F, A>"), new Edge(4, "<F, E>"), new Edge(6, "<F, G>")]),  // 5
        new Vertex("G", [new Edge(1, "<G, B>"), new Edge(3, "<G, D>"), new Edge(5, "<G, F>"), new Edge(7, "<G, H>")]),  // 6
        new Vertex("H", [new Edge(3, "<H, D>"), new Edge(4, "<H, E>"), new Edge(6, "<H, G>"),]),  // 7
        new Vertex("I", [new Edge(1, "<I, B>"), new Edge(2, "<I, C>"), new Edge(3, "<I, D>"),]),  // 8
    ];

    let graphAjacencyList: GraphAjacencyList = new GraphAjacencyList(vertexesAjacencyList);

    console.log("图的深度优先搜索（邻接矩阵表示法）：");
    dfs1(graph);

    console.log("图的深度优先搜索（邻接表表示法）：");
    dfs2(graphAjacencyList);

    console.log("图的广度优先搜索（邻接矩阵表示法）：");
    bfs1(graph);

    console.log("图的广度优先搜索（邻接表表示法）：");
    bfs2(graphAjacencyList);
}

main();

注意：对于tsc编译器可使用下面的命令来编译上面的TypeScript代码，否则会报错误：TS1056: Accessors are only available when targeting ECMAScript 5 and higher.更早版本的ES不支持访问器（getter/setter）。

tsc graphDfsBfs.ts -t es6

在终端中使用node来运行被tsc编译成js后的代码。

node graphDfsBfs.js

参考资料：

《大话数据结构》（溢彩加强版） - 程杰 著 - 清华大学出版社 - P203