Paillier半同态加密：原理高效实现方法和应用

Posted 2021-10-28 Pam

转载：https://developer.aliyun.com/article/793131?spm=a2c6h.14164896.0.0.ad7272aaWdeABj&accounttraceid=46c7d08131124413aff4241ff487527bbfbo

一 简介

1 背景

《数据安全法》已于9月1日起正式实施，两个月后《个人信息保护法》也将开始施行，意味着数据安全和隐私保护方面的监管将会在年内陆续到位。 在合规收紧大背景下，“数据孤岛”现象日渐明显。如何实现安全的数据流通，保护数据隐私并发挥数据的价值，支持多方的联合计算，是各大数据平台亟需解决的问题。而隐私计算技术旨在实现“数据可用不可见”的目标，具有广阔的应用前景。在联合国隐私增强计算技术手册[35]中，列出了同态加密（Homomorphic Encryption, HE）、安全多方计算（Secure Multiparty Computation, MPC）等5种隐私计算技术，其中HE提供了对加密数据进行处理的能力，完美符合隐私计算的计算模式，是当前学术研究的热点，受到了广泛的关注。

2 何为同态加密（HE）？

HE是一种特殊的加密方法，它允许直接对加密数据执行计算，如加法和乘法，而计算过程不会泄露原文的任何信息。计算的结果仍然是加密的，拥有密钥的用户对处理过的密文数据进行解密后，得到的正好是处理后原文的结果。

根据支持的计算类型和支持程度，同态加密可以分为以下三种类型：

• 半同态加密（Partially Homomorphic Encryption, PHE）：只支持加法或乘法中的一种运算。其中，只支持加法运算的又叫加法同态加密（Additive Homomorphic Encryption, AHE）；
• 部分同态加密（Somewhat Homomorphic Encryption, SWHE）：可同时支持加法和乘法运算，但支持的计算次数有限；
• 全同态加密（Fully Homomorphic Encryption, FHE）：支持任意次的加法和乘法运算。

在同态加密概念被Rivest在1978年首次提出[15]后，学术界出现了多个支持PHE的方案，如RSA、GM[13]、Elgamal[14]、Paillier[1]。此后，SWHE方案也相继问世，如BGN[16]。关于FHE如何实现，学术界在很长的时间都没有答案。直到2009年，Gentry[28]使用理想格构造了第一个FHE方案，轰动了整个学术界，并引发了学者们对于FHE方案构造的研究热潮。此后相继涌现出多个优秀的FHE方案，包括BFV[36]、BGV[37]、CKKS[38]等，以及多个优秀的开源算法库如SEAL[39]、HELib[40]等。

3 为何需要半同态加密（PHE）？

通用安全计算方法有所不足

隐私计算的应用场景非常广泛，除满足多方的通用计算（算数或布尔计算）功能外，还有如隐私集合求交(Private Set Intersection, PSI)[17]、隐私保护机器学习[4]、加密数据库查询[9]、门限签名[3]等等更加细分的应用。然而，在几种主要的通用计算技术路线中，每种方法各有各的效率/安全性缺陷。FHE在计算有限次乘法后需要较复杂的去除噪声的操作，经典的通用MPC协议通信开销较大，而TEE的安全性高度依赖于硬件厂商，无法提供密码学上严谨的安全性。在复杂的计算场景中，单独使用某种通用方法通常得不到一个可用的落地方案，这也激发了学者们研究对于特定场景的特定解法。一个可行的方案通常是根据具体场景来进行定制化的设计，通过组合、优化不同的技术组件来得到安全、高效的方案，精准满足该场景需求。

PHE登场：辅助多种隐私计算场景

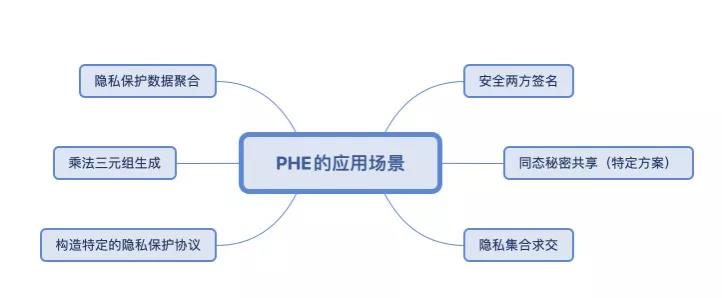
图1.1. PHE的应用场景

由于通用安全计算方法的一些不足，以及在一些特定场景只需要使用一种HE运算（如加法）即可完成功能，PHE在隐私计算领域得到了大量使用，在多个开源库（如FATE[31]）和大量学术顶会（如S&P、NDSS等41811）的方案中都有它的身影。PHE的高效、支持无限次加法或乘法的特点，使其成为隐私计算的重要基本组件，可辅助完成多种隐私计算功能：

1）隐私保护数据聚合

由于加法PHE可以在密文上直接执行加和操作，不泄露明文，在到多方协作的统计场景中，可完成安全的统计求和的功能。

• 在联邦学习中，不同参与方训练出的模型参数可由一个第三方进行统一聚合。使用加法PHE，可以在明文数据不出域、且不泄露参数的情况下，完成对模型参数的更新，此方法已应用在实际应用（如FATE[31]）和多个顶会工作中（如SIGMOD[4]、KDD[7]、ATC[18]）；
• 在在线广告投放的场景中，广告主（如商家）在广告平台（如媒体）投放在线广告，并希望计算广告点击的转化收益。然而，广告点击数据集和购买数据集分散在广告主和广告平台两方。使用PHE加密结合隐私集合求和（Private Intersection-Sum-with-Cardinality, PIS-C)协议[19]可以在保护双方隐私数据的前提下，计算出广告的转化率。 该方案已被Google落地应用[20]；
• 在加密数据库SQL查询场景，在数据库不可信的情况下，可以通过部署协议和代理来保护请求者的查询隐私。其中，PHE可以用来完成安全数据求和和均值的查询[9]。

2）乘法三元组生成

通用安全计算根据计算电路的不同可分为算数计算和布尔计算，对于算数计算来说，其中的难点是如何做乘法。而使用预生成的乘法三元组来辅助乘法运算的方法可以大大降低乘法的在线开销，是目前最为流行的方法。PHE是用于计算乘法三元组的重要工具2，已在多个顶会方案（如NDSS[11]、S&P[21]）和实际产品（如Sharemind[2]）中得到应用，对于加速安全计算具有重要意义。

3）构造特定的隐私保护协议

在机器学习预测分类场景中，若拥有模型的一方不可信（如外部厂商），在数据方输入样本进行预测分类时，可能需要保护样本数据的隐私。PHE作为building block可以构造出隐私保护比较协议和argmax协议，并可以此进一步构造出隐私保护朴素贝叶斯分类器和超平面决策分类器[24]。此外，用PHE还可构造出不经意选择（Oblivious Selection）协议，来支持隐私保护决策树分类器[25]。

4）门限签名

传统签名方式要求签名时从存储介质（如磁盘）中拉取完整私钥到内存，存在泄露风险（如被木马、病毒窃取，侧信道攻击等）。 使用门限签名可以有效规避此类风险，让多方协作完成签名过程，并确保私钥没有在任何一方被恢复。特定的PHE算法可以用于实现门限签名[3]，相关方案已在集团密钥管理系统落地[22]。

5）同态秘密分享

同态秘密分享是一种前沿的安全计算技术，可以用来大幅降低安全计算的交互通信量。具有特定代数结构的PHE方案经过特殊设计，可以用来实现同态秘密分享[10]，具有广阔的应用前景。

6）隐私集合求交

使用PHE结合多项式的方法可构造出PSI协议[17]。

4 Paillier：最著名的半同态加密方案

Paillier是一个支持加法同态的公钥密码系统 [1]，由Paillier在1999年的欧密会（EUROCRYPT）上首次提出。此后，在PKC\'01中提出了Paillier方案的简化版本26，是当前Paillier方案的最优方案。在众多PHE方案中，Paillier方案由于效率较高、安全性证明完备的特点，在各大顶会和实际应用中被广泛使用，是隐私计算场景中最常用的PHE实例化方案之一。

其他的支持加法同态的密码系统还有DGK [5]、OU [6]和基于格密码的方案[12]等。其中，DGK方案的密文空间相比Paillier更小，加解密效率更高，但由于算法的正确性和安全性在学术界没有得到广泛研究和验证，且我们的实验表明算法的加解密部分存在缺陷，不推荐在工业界代码中使用。OU和基于格的加法同态计算效率更高，也是PHE不错的候选项。其中OU的在方案中的使用频率相对较低，而基于格的方案密文大小较大，在一些特定场景有自身的优势。

数据技术及产品部-数据安全生产平台团队对Paillier加密方案的原理和高效实现方法开展了研究，利用多种优化方法实现了目前最优的Paillier加解密效率，可助力基于Paillier加密的上层协议在集团真实业务场景中落地。

二 Paillier方案原理

1 加法同态加密定义

在描述具体方案之前，我们先定义加法PHE。首先列举方案具有的所有算法。

• KeyGen()：密钥生成算法。用于产生加密数据的公钥PK（Public Key）和私钥SK（Secret Key），以及一些公开常数PP（Public Parameter）；
• Encrypt()：加密算法。使用PK对用户数据Data进行加密，得到密文CT（Ciphertext）；
• Decrypt()：解密算法。用于解密得到数据原文PT（Plaintext）。

HE除了加解密以外，还具有在密文上进行处理的能力，所以还应拥有“处理”算法。对于加法PHE，支持的算法有同态加以及同态标量乘（标量乘法可看作多次加法）。

• Add()：同态加算法。输入两个CT进行同态加运算。
• ScalaMul()：同态标量乘算法。输入一个CT和一个标量PT，计算CT的标量乘结果。

2 Paillier方案描述

原版Paillier方案于论文[1]中提出，下面对方案进行描述：

密钥生成

 

加密

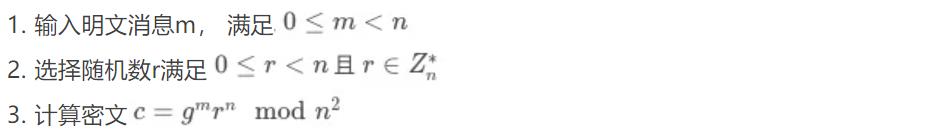
解密

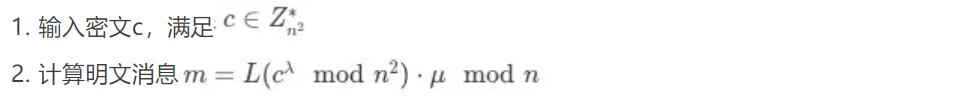
同态加

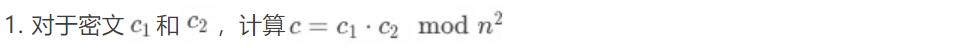
同态标量乘

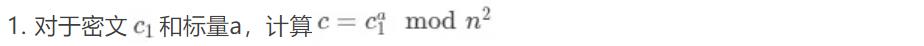
3 正确性和安全性

加解密正确性

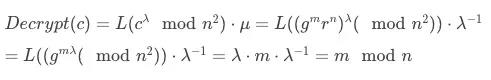
同态加正确性

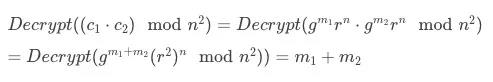
同态标量乘正确性

安全性

Paillier方案满足加密方案的标准安全定义：语义安全，即在选择明文攻击下的密文的不可区分性（IND-CPA）。直观地说，就是密文不会泄露明文中的任意信息。方案安全性可以归约到判定性合数剩余假设（Decisional Composite Residuosity Assumption, DCRA），即给定一个合数n和整数z，判定z是否在n^2下是否是n次剩余是困难的。这个假设经过了几十年的充分研究，到目前为止还没有多项式时间的算法可以攻破，所以Paillier加密方案的安全性被认为相当可靠。

详细的安全性证明可以参见论文，这里不再赘述1。

三 高效实现

1 优化参数选择

根据论文 [23]中的描述，在不影响算法正确性的前提下，为了简化运算，算法在密钥生成阶段可以取g=n+1。此后，加密过程中的计算g^m的部分可进行如下简化：

对于g^m=(n+1)^m， 根据二项定理[43]，由于：

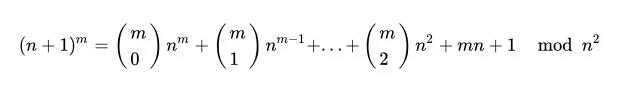
前m-1项均是n^2的倍数，在模n^2下消去，故这里模指数运算简化为了1次模乘，加速了加密过程：

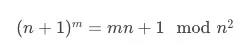
2 使用Paillier-DJN优化方案

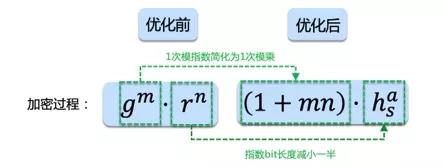
图3.1 优化1和优化2

3 使用中国剩余定理（CRT）加速模指数

定理介绍

使用CRT计算模指数过程举例

CRT应用到Paillier加解密过程

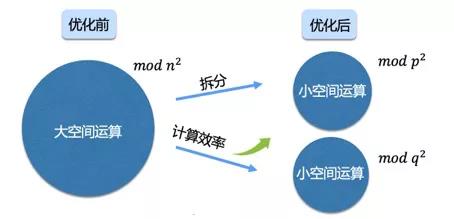
图3.2 使用CRT进行优化

若使用CRT进行计算加速，计算方必需要知道模数n^2的分解(p^2、q^2)。而(p^2、q^2)为私钥的部分，故我们可以直接将CRT应用到解密过程。 而对于加密过程来说，我们根据加密者是否拥有私钥，将加密算法设计为两类，分别为公钥加密算法Enc1(pk,m)和私钥加密算法Enc2(pk,sk,m)。若加密消息的一方只拥有公钥，则调用标准的公钥加密算法Enc1(pk,m)进行加密；若加密的一方同时拥有公钥和私钥，则可以调用私钥加密算法Enc2(pk,sk,m)，输入私钥的(p^2、q^2)来使用CRT加速加密过程。

我们对使用CRT后的优化效果进行测试。由于DJN方案严格优于Paillier原版方案，我们只将CRT应用到DJN。经测试，使用CRT后，DJN的私钥加密和解密性能提升约90%，具体数据见表4.2。

4 预计算

• 对于fixed-base情况，进行指数预计算来加速模乘

在Java上，若使用上述按单个bit展开的方法，|n|/2次（|n|=3072）耗时比1次模指数要长，没有达到优化计算的效果。

在存储空间有限时，可以采用更轻量级的预计算方法来减小存储开销41，在c/c++下预计可以达到一定加速效果。
这里的模乘我们使用Java中的Biginteger.multiply()，模指数使用Biginteger.modpow()。

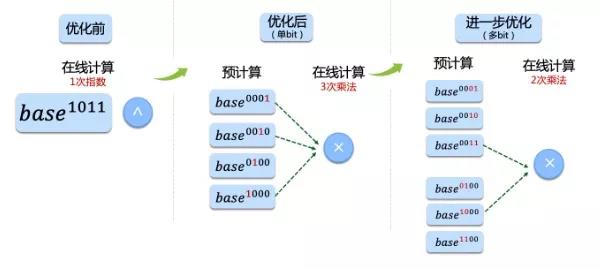
图3.3 预计算

• 在加解密时会重复用到的变量，都在密钥生成过程提前计算并保存，以避免加解密时的重复运算。

5 使用JNI技术

Java执行复杂计算的效率通常不及C/C++。以密码学计算中常见的模指数为例，在设置模数n、底数b和指数e均为2048bits的情况下，在Java中执行1000次Biginteger.modPow()需要耗时3000ms，而在C++下使用GMP库的mpz_powm()跑只需1800ms，相比Java，性能提升了约60%。 我们希望可以把Paillier中耗时的加解密计算通过调用C++执行来提速。

Java 本地接口（Java Native Interface, JNI）是Java语言的本地编程接口，它提供了若干的API，使得Java可以与其他语言（如C/C++）程序进行互相调用，来实现Java不便实现的功能或难以达到的效率。

有了JNI这座桥梁，我们就可以将复杂耗时的计算模块用效率更高的C/C++实现，通过JNI来实现Java对算法的高效调用。我们对原版Paillier方案和优化后的Djn算法都开发了JNI调用的版本，用C++编写核心算法，并通过Java包装类使用JNI对C++库进行调用。应用JNI后，加解密过程的效率获得了显著提升，具体数据见表4.2。

使用JNI调用C++库提升效率的代价是会丧失程序的可移植性（C/C++是非跨平台语言），故是否使用JNI要根据场景灵活选择。

图3.4 JNI

6 打包

为了确保安全强度，Paillier方案中的明文空间大小为固定的n（如3072bits），而待加密的明文可能属于较小的空间（如16bits）。在这种情况下，如果按照正常的加密方式，将1个明文加密为1个密文，则明文空间会存在很高的冗余（等同于先在16bits明文的高位填充0，编码到3072bits，再进行加密），在加密时间和空间上效率都很低。

为了避免冗余，在明文较短且定长的情况下，我们充分利用明文空间，将多个明文打包为1个进行加解密 2。具体过程如下：

相比原来的1次只加密1个明文，使用打包优化后，密文大小和加解密中的模指数时间消耗降低为原来的1/k。该优化的效果取决于明文长度，本文中暂不作实验测试。

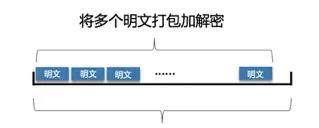
图3.5 打包

四 测试结果

1 测试条件

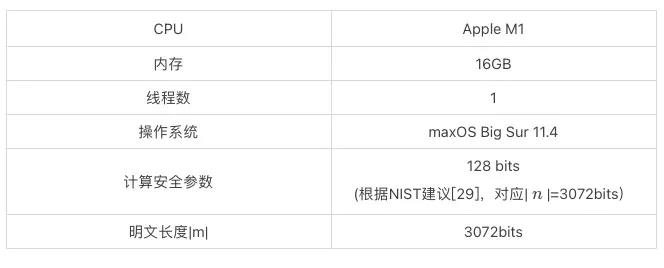
表4.1. 测试条件

2 性能

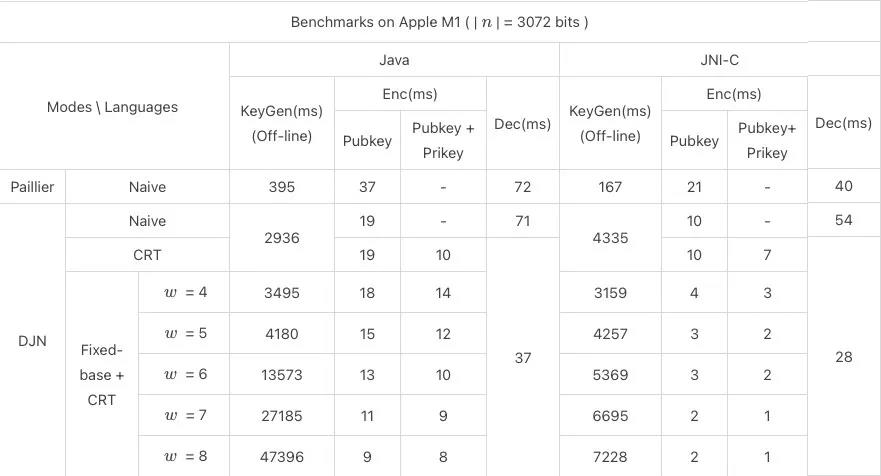
表4.2：Paillier密钥生成、加密、解密性能在不同优化下的表现

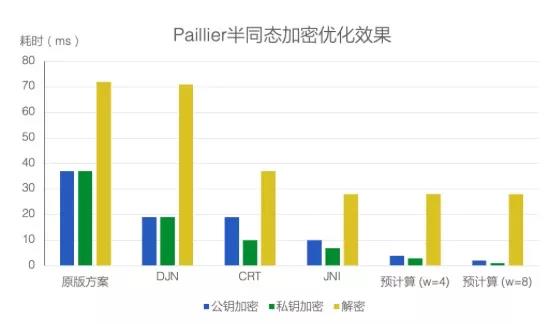
图4.1 Paillier半同态加密优化效果

从表4.2和图4.1中可以看到，DJN优化方案加解密的效率相比原版方案提升了大约100%。当使用CRT优化后，私钥加密和解密的效率继续提升约90%。当CRT和Fixed-base预计算同时使用时，随着窗口大小w的增大，公钥加密的效率进一步提升；使用JNI调用C同样可以大大降低计算开销，相比纯Java提升幅度达60%以上，提升幅度在结合使用Fixed-base优化时尤为明显。特别地，当同时使用DJN+CRT+Fixed-base（w=8）+JNI优化时，公/私钥加密的时间消耗从原版方案的37ms，分别下降到约2ms/1ms，实现了质的飞跃。随着不同优化的运用，密钥生成（预计算）的时间会随着变长，但该部分为一次性消耗，相比大量数据的加解密时间可以忽略不计。

3 预计算List大小

使用Fixed-base预计算优化需要提前生成预计算list，list占用的空间大小与窗口大小w的大小见表4.3。

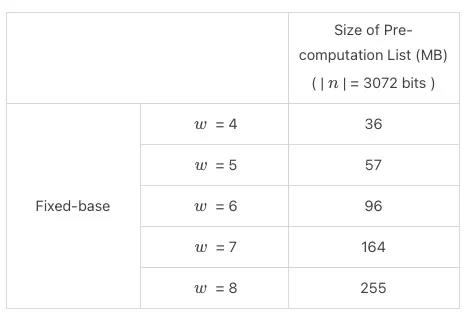
表4.3：Paillier预计算List的大小与窗口大小w的关系

五 与现有开源库的对比

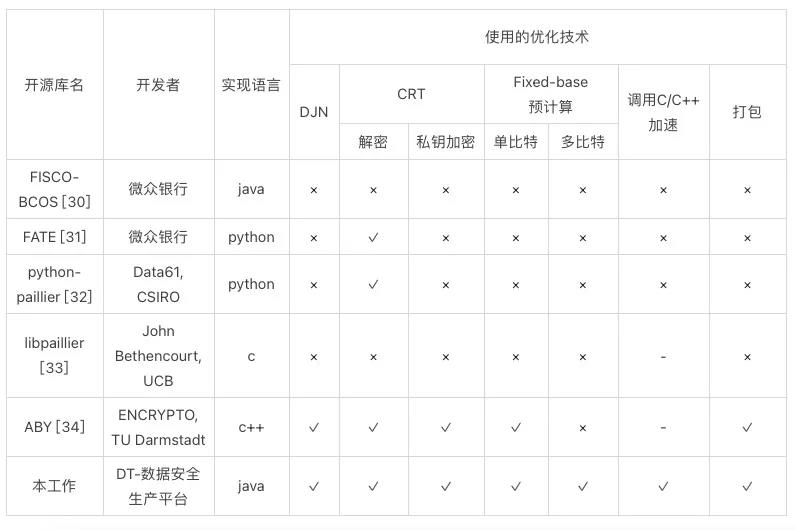
表5.1. 本工作与一些现有开源库的对比

六 PHE的应用：一个实际的例子

1 业务场景

在商业广告的在线投放场景中，广告主（如商家）在广告平台（如媒体平台）上投放广告曝光产品，而用户点击广告后可能会产生购买行为，实现广告转化变现。为了评估广告在该平台投放的实际收益，需要统计在点击了广告的用户中，共产生了多少消费金额。然而，“点击广告”的用户数据集在广告平台侧，而“发生购买”的用户数据集在广告主侧。 由于法律合规和商业机密因素的影响，双方可能不愿意分享原文数据进行合作。

2 隐私诉求

• 不能泄露双方交集的个体用户信息，否则不满足法律规定的“最小够用”原则，故“先进行PSI再求和”的方法不可取。
• 不能泄露交易金额给广告平台方。

3 解法：Private Intersection-Sum-with-Cardinality （PIS-C）

PIS-C协议[19]于在EuroS&P\'20会议上被提出，其核心思想是通过"Tag, Shuffle and Aggregate"过程，将PSI协议和PHE转化为PIS-C协议，使得广告主最终得到交集value的聚合结果，确保没有额外数据泄露（具体过程参见原论文）。

 

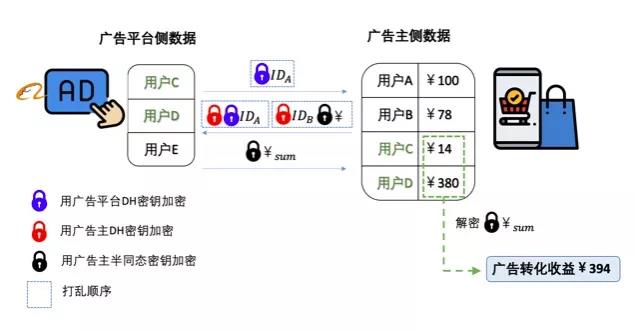
图6.1. 基于DDH的PIS-C协议流程

PHE在该协议中扮演着核心作用。协议中的“隐私保护求和”功能依赖于广告主将自己的交易数据用PHE加密发送给广告平台， 使得广告平台在看不到原始数据的前提下，完成对交集中数据金额的聚合。该方案已被Google落地[20]。除了广告场景外，还可以用于多种“行为数据和效益数据分离”的商业场景，在应用上有着很大的想象空间。

七 关于我们

数据技术及产品部-数据安全生产平台致力于前沿隐私计算技术的研究与落地，与阿里云共同研发的DataTrust隐私计算产品是信通院大数据产品能力测评中唯一同时获得“多方安全计算”、“可信执行环境”、“联邦学习”等4项测评通过的产品，已服务于经济体内外多个实际业务。如有隐私计算相关的技术合作意愿/业务需求/转岗意愿，欢迎垂询。

参考文献

[1] Paillier P. Public-key cryptosystems based on composite degree residuosity classes[C]//International conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 1999: 223-238.
[2] Pullonen P, Bogdanov D, Schneider T. The design and implementation of a two-party protocol suite for Sharemind 3[J]. CYBERNETICA Institute of Information Security, Tech. Rep, 2012, 4: 17.
[3] Lindell Y. Fast secure two-party ECDSA signing[C]//Annual International Cryptology Conference. Springer, Cham, 2017: 613-644.
[4] Fu F, Shao Y, Yu L, et al. VF2Boost: Very Fast Vertical Federated Gradient Boosting for Cross-Enterprise Learning[C]//Proceedings of the 2021 International Conference on Management of Data. 2021: 563-576.
[5] Damgård I, Geisler M, Krøigaard M. Efficient and secure comparison for on-line auctions[C]//Australasian conference on information security and privacy. Springer, Berlin, Heidelberg, 2007: 416-430.
[6] Okamoto T, Uchiyama S. A new public-key cryptosystem as secure as factoring[C]//International conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 1998: 308-318.
[7] Chen C, Zhou J, Wang L, et al. When homomorphic encryption marries secret sharing: Secure large-scale sparse logistic regression and applications in risk control[J]. arXiv preprint arXiv:2008.08753, 2020.
[8] Damgård I, Jurik M, Nielsen J B. A generalization of Paillier’s public-key system with applications to electronic voting[J]. International Journal of Information Security, 2010, 9(6): 371-385.
[9] Popa R A, Redfield C M S, Zeldovich N, et al. CryptDB: Protecting confidentiality with encrypted query processing[C]//Proceedings of the Twenty-Third ACM Symposium on Operating Systems Principles. 2011: 85-100.
[10] Orlandi C, Scholl P, Yakoubov S. The Rise of Paillier: Homomorphic Secret Sharing and Public-Key Silent OT[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, Cham, 2021: 678-708.
[11] Demmler D, Schneider T, Zohner M. ABY-A framework for efficient mixed-protocol secure two-party computation[C]//NDSS. 2015.
[12] Rathee D, Schneider T, Shukla K K. Improved multiplication triple generation over rings via RLWE-based AHE[C]//International Conference on Cryptology and Network Security. Springer, Cham, 2019: 347-359.
[13] Shafi G, Silvio M. Probabilistic encryption & how to play mental poker keeping secret all partial information[C]//Proceedings of the 14th Annual ACM Symposium on Theory of Computing. 1982: 365-77.
[14] ElGamal T. A public key cryptosystem and a signature scheme based on discrete logarithms[J]. IEEE transactions on information theory, 1985, 31(4): 469-472.
[15] Rivest R L, Adleman L, Dertouzos M L. On data banks and privacy homomorphisms[J]. Foundations of secure computation, 1978, 4(11): 169-180.
[16] Boneh D, Goh E J, Nissim K. Evaluating 2-DNF formulas on ciphertexts[C]//Theory of cryptography conference. Springer, Berlin, Heidelberg, 2005: 325-341.
[17] Freedman M J, Nissim K, Pinkas B. Efficient private matching and set intersection[C]//International conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 2004: 1-19.
[18] Zhang C, Li S, Xia J, et al. Batchcrypt: Efficient homomorphic encryption for cross-silo federated learning[C]//2020 {USENIX} Annual Technical Conference ({USENIX}{ATC} 20). 2020: 493-506.
[19] Ion M, Kreuter B, Nergiz A E, et al. On deploying secure computing: Private intersection-sum-with-cardinality[C]//2020 IEEE European Symposium on Security and Privacy (EuroS&P). IEEE, 2020: 370-389.
[20] https://security.googleblog.com/2019/06/helping-organizations-do-more-without-collecting-more-data.html
[21] Mohassel P, Zhang Y. Secureml: A system for scalable privacy-preserving machine learning[C]//2017 IEEE symposium on security and privacy (SP). IEEE, 2017: 19-38.
[22] https://zhuanlan.zhihu.com/p/76158563
[23] Catalano D, Gennaro R, Howgrave-Graham N, et al. Paillier\'s cryptosystem revisited[C]//Proceedings of the 8th ACM Conference on Computer and Communications Security. 2001: 206-214.
[24] Bost R, Popa R A, Tu S, et al. Machine learning classification over encrypted data[C]//NDSS. 2015, 4324: 4325.
[25] Kiss Á, Naderpour M, Liu J, et al. SoK: Modular and efficient private decision tree evaluation[J]. Proceedings on Privacy Enhancing Technologies, 2019.
[26] Damgård I, Jurik M. A generalisation, a simplification and some applications of Paillier\'s probabilistic public-key system[C]//International workshop on public key cryptography. Springer, Berlin, Heidelberg, 2001: 119-136.
[27] Acar A, Aksu H, Uluagac A S, et al. A survey on homomorphic encryption schemes: Theory and implementation[J]. ACM Computing Surveys (CSUR), 2018, 51(4): 1-35.
[28] Gentry C. A fully homomorphic encryption scheme[M]. Stanford university, 2009.
[29] https://www.keylength.com/en/4/
[30] https://github.com/FISCO-BCOS/paillier-lib
[31] https://github.com/FederatedAI/FATE
[32] https://github.com/data61/python-paillier
[33] http://hms.isi.jhu.edu/acsc/libpaillier/
[34] https://github.com/encryptogroup/ABY
[35] Big Data UN Global Working Group. Un handbook on privacy-preserving computation techniques[J]. 2019.
[36] Fan J, Vercauteren F. Somewhat practical fully homomorphic encryption[J]. IACR Cryptol. ePrint Arch., 2012, 2012: 144.
[37] Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory (TOCT), 2014, 6(3): 1-36.
[38] Cheon J H, Kim A, Kim M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2017: 409-437.
[39] https://github.com/microsoft/SEAL
[40] https://github.com/homenc/HElib
[41] Brickell E F, Gordon D M, McCurley K S, et al. Fast exponentiation with precomputation[C]//Workshop on the Theory and Application of of Cryptographic Techniques. Springer, Berlin, Heidelberg, 1992: 200-207.
[42] Lim C H, Lee P J. More flexible exponentiation with precomputation[C]//Annual International Cryptology Conference. Springer, Berlin, Heidelberg, 1994: 95-107.
[43] https://en.wikipedia.org/wiki/Binomial_theorem
[44] https://en.wikipedia.org/wiki/Chinese_remainder_theorem
[45] https://en.wikipedia.org/wiki/Euler%27s_theorem
[46] https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity

---

 

作者： Pam

出处： https://www.cnblogs.com/pam-sh/>

关于作者：网安在读

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出, 原文链接 如有问题， 可邮件（[e-mail]）咨询.

同态加密之Paillier算法

同态加密之Paillier算法

0，背景介绍

同态加密，即原来在明文上的运算操作，经过同态加密后在密文上同样可以进行。一般有半同态和全同态加密之分：

• 半同态加密 （Partial Homomorphic Encryption, PHE）：只支持某些特定的运算法则 f ,PHE 的优点是原理简单、易实现，缺点是仅支持一种运算(加法或乘法)；

• 层次同态加密（Liveled HE，LHE）：一般支持有限次数的加密算法,LHE 的优点是同时支持加法和乘法，并且因为出现时间比 PHE 晚，所以技术更加成熟、一般效率比 FHE 要高很多、和 PHE 效率接近或高于 PHE，缺点是支持的计算次数有限。

• 全同态加密 （Fully Homomorphic Encryption, FHE）：支持无限次的任意运算法则 f，FHE 有以下类别：基于理想格的 FHE 方案、基于 LWE/RLWE 的 FHE 方案等等。FHE 的优点是支持的算子多并且运算次数没有限制，缺点是效率很低，目前还无法支撑大规模的计算。

  第一个满足加法和乘法同态的同态加密方法直到2009年才由Craig Gentry提出。目前来说，全同态加密算法性能较差，应用较少。比较常用的是半同态加密算法，实现方式有 RSA （乘法同态）、Elgamal、Paillier （加法同态）等。

1，Paillier算法介绍

密钥生成

1. 随机选择两个质数 p 和 q 满足 gcd(pq,(p-1)(q-1)) =1，这个条件保证了 p 和 q 的长度相等；
2. 计算 N=pq 和 λ=lcm(p−1,q−1)，其中 lcm 表示最小公倍数；
3. 随机选择 g∈Z∗N^2，满足 $gcd(L(g^{\lambda }mod{N}^2),N)=1$，后面会发现这里的 g=n+1。其中 Z 表示整数，下标表示该整数集合里有多少个元素；L(x)=$\frac{x-1}{N}$， $\mu =(L(g^{\lambda }mod{N}^2){)}^{-1}\mathrm{m}\mathrm{o}\mathrm{d}N$；
4. 公钥为 (N,g)；
5. 私钥为(λ,μ)。

加密过程

对于任意明文消息 $m\in Z_N$，任意选择一随机数 $r\in Z_N^{\ast }$，计算得到密文 c ：

$c=E(m)=g^m{r}^N\mathrm{m}\mathrm{o}\mathrm{d}{N}^2$

解密过程

对于密文$ c∈Z_N²*$，计算得到明文 m ：

$m=D(c)=\frac{L(c^{\lambda }mod{N}^2)}{L(g^{\lambda }mod{N}^2)}\mathrm{m}\mathrm{o}\mathrm{d}N=L(c^{\lambda }mod{N}^2)\ast \mu \mathrm{m}\mathrm{o}\mathrm{d}N$

加法同态的性质

对于任意明文 $m1，m2\in Z_N$和任意$r1，r2\in Z_N^{\ast }$，对应密文$c1=E[m1,r1]，c2=E[m2,c2]$满足：

$c_1\cdot c_2=E\left[m_1,r_1\right]\cdot E\left[m_2,r_2\right]=g^{m_1+m_2}\cdot {\left(r_1\cdot r_2\right)}^N\mathrm{m}\mathrm{o}\mathrm{d}{N}^2$

解密后得到：

$D\left[c_1\cdot c_2\right]=D\left[E\left[m_1,r_1\right]\cdot E\left[m_2,r_2\right]\mathrm{m}\mathrm{o}\mathrm{d}{N}^2\right]=m_1+m_2\mathrm{m}\mathrm{o}\mathrm{d}N$

即我们得到了：$c1\ast c2=m1+m2$。密文乘等于明文加。

通过分析发现，密文乘时，含有的明文是在指数上相加的，所以解密后就可以得到明文相加结果。

为什么叫加法同态呢？我们一般希望密文计算的结果和我们明文计算的结果相同，所以对于密文上是如何计算的不做要求。这时我们在明文上实现了加法的目的，就叫它加法同态。由此还扩展出了同态加和标量乘的性质。

算法理论

由上式结论不难知道：$\mu ={\lambda }^{-1}$（g=n+1）。此外，还有 $r^{\lambda n}\mathrm{m}\mathrm{o}\mathrm{d}{N}^2=1$。

具体算法理论证明，参见：Paillier Cryptosystem理论与实践

2，pyhtotn—paillier算法演示

我们使用了 Python 实现的 paillier 算法来演示一些性质。你可以使用如下命令安装对应库：

pip install phe

具体使用可以参考：https://python-paillier.readthedocs.io/en/latest/usage.html

下面，我们使用 phe 演示 paillier 的同态加和标量乘的性质：

from phe import paillier # 开源库
import time # 做性能测试

# 测试paillier参数
print("默认私钥大小：",paillier.DEFAULT_KEYSIZE) #2048
# 生成公私钥
public_key,private_key = paillier.generate_paillier_keypair()
# 测试需要加密的数据
message_list = [3.1415926,100,-4.6e-12]
# 加密操作
time_start_enc = time.time()
encrypted_message_list = [public_key.encrypt(m) for m in message_list]
time_end_enc = time.time()
print("加密耗时ms：",time_end_enc-time_start_enc)
# 解密操作
time_start_dec = time.time()
decrypted_message_list 同态加密之Paillier算法

 京东云开发者｜经典同态加密算法Paillier解读 - 原理实现和应用
 经典同态加密算法Paillier解读 - 原理实现和应用
 资源防丢失
 资源防丢失
 联邦学习安全防御之同态加密