机器学习笔记

Posted 2021-04-03 数字自修

前情提要

想开个话题，整理下前段时间学的机器学习。

基本术语和概念

机器学习：在没有明确设定的情况下，使计算机具有学习的能力。

样本：所研究对象的一个个体。

样本集：若干样本构成的集合。

标记(标签)：样本的“结果”信息。比如二分类问题中，一个样本属于正类(1)还是负类(0)。

特征(属性)：研究对象在某方面的性质。

属性值：属性上的取值，也叫特征值。

分类：需要预测的输出为离散值。

回归：需要预测的输出为连续值。

聚类：将训练集中的样本分成若干组,每组称为一个 “簇”。

机器学习的一般流程是，针对某一个问题，给出海量大的数据(样本集)，设计一个算法，输入这些数据，得出一个模型，然后用这个模型去预测未来更多与之相关的东西。比如最常见的人脸识别(很多人脸识别算法属于深度学习，此为后话)，首先需要有几万甚至千万上亿的人脸图片作为输入，然后算法提取人脸的各项特征，得出模型；等再输入图片时，就会判别是否是人脸、是否是某个人。

机器学习的算法分为两类：

1 监督学习：是指通过让机器学习大量带有标签的样本数据，训练出一个模型，并使该模型可以根据输入得到相应输出的过程。监督学习的训练集要求包括输入和结果。比如预测房价，首先要有海量的数据，所在城市规模、房子大小、楼层数等多个特征，这些特征上的取值即为输入(x)，这些特征组合起来对应的房价是多少，这就是结果(y)；算法根据这些输入，输出一个模型，可做预测。输入监督学习分为：回归问题和分类问题。

2 无监督学习：输入数据没有被标记，也没有确定的结果。样本数据类别未知，需要根据样本间的相似性对样本集进行分类(聚类)，试图使类内间距最小化，类间间距最大化。

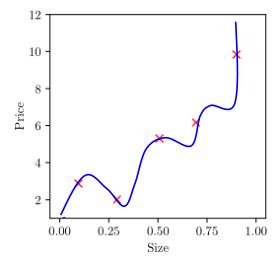
欠拟合：指在训练集、测试集上均表现不佳的情况。解决方法：回归模型可以添加更多高次项、增加神经网络层数、增加更多特征等，下图是个欠拟合的例子，可见蓝线的预测能力较差，大部分数据没有拟合到。

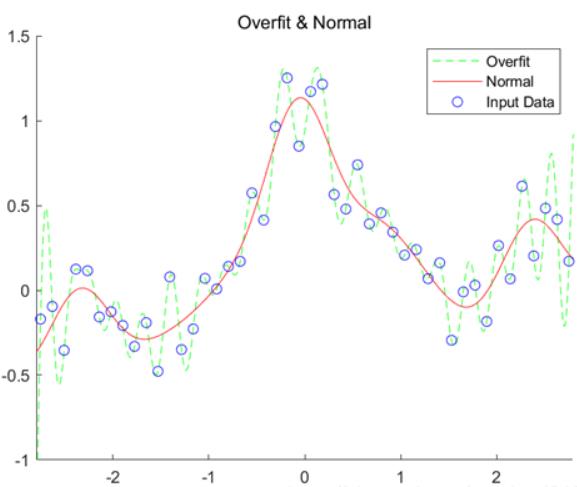
过拟合：指模型在训练集上表现很好，到了验证和测试阶段就大不如意了，即模型的泛化能力很差。解决：增加训练数据数、减少特征数、使用正则化约束等，下图是个过拟合例子，过拟合在样本集表现优秀，但脱离了样本就歇逼了。

下图中，圆圈为样本点，显然红色线是我们期待的结果，绿色虚线是过拟合情况。

假设函数：对所面临的问题，选择一个适当的模型。比如对于一个线性模型，可设为：

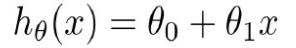
其中，x是自变量，θ0和θ1都是参数，这两个参数需要用算法得出，得出这两个参数后，整个模型也就确定了。非线性情况类似。

代价函数：

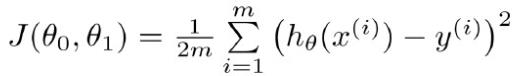
其中，括号里，函数hθ是我们得出的模型，x(i)是第i个样本的输入特征值（就是某事物的各项指标），y(i)是样本中对应x(i)的输出，m是样本的个数。

关于原理，举个例子：

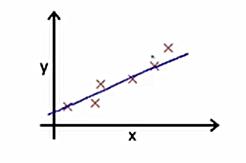
下图中，×为样本点，直线是得出的模型。那怎么衡量这个模型的好坏呢？如果模型好，说明有大部分数据样点在这条直线上；如果不好，那么样本点会离这条线远远的。这也就是上式的意义，括号的平方算出了每个样本点距离这条直线的垂直距离（因为正、负都是偏离直线，所以取平方，不用考虑正负），将m个样本的偏离加起来，就可得到总的偏离（偏离越小，说明模型越好）。前面本应是m分之1，因为后面用梯度下降算法求参数时，会对整个式子求导，平方求导之后会多出来个2，所以前面是2m分之1，方便消去这个2，而且加上一个2对整体优化效果是没有影响的。

代价函数J的自变量之所以是θ0和θ1，是因为将函数h代入代价函数后，由于x和y都是样本里的数据，这是已知的，未知的就是那两个参数，这两个参数决定假设函数即模型的好坏。

我们的目的便是求出当代价函数最小时，θ0和θ1的值，因为代价函数最小时，也就是最好的模型，更有预测能力。

目的：

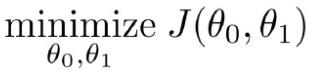
举个最简单的例子，假设函数只有一个参数：

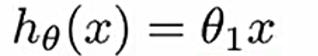
对应的代价函数：

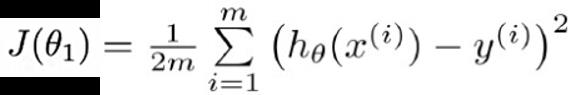
把函数hθ代入，可得一个一元二次方程。对于假设函数，如果预计的结果如下：

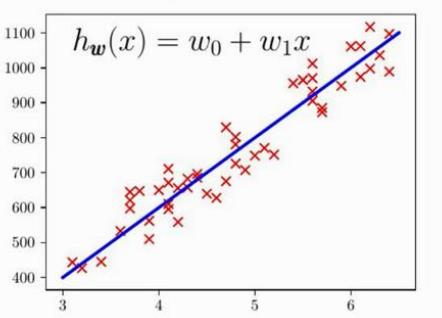
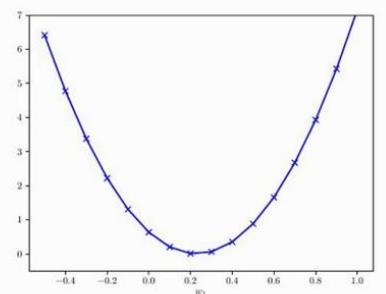
则对应的代价函数如下，是个参数为θ的二次函数。此处需设计的算法，就是根据很多样本，找出在这个二次函数最低点处，对应的参数θ的值。

因为该函数(代价函数)的最低点，代表样本点和假设函数(hθ)的差距最小，即在最低点时，模型最好，最能说明问题，最能预测数据的变化趋势。所以需要找出最低点对应的参数θ。

上面是一个参数的例子，下面是有两个参数的例子：

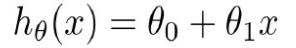
对应的代价函数：

这是一个有两个参数（θ0和θ1）的二维曲面：

对于这种情况，则是找曲面最低点，对应的两个参数值。

以上配图来自网络整理，侵权删。