左旋转右旋转双旋

Posted 2021-10-27 一乐乐

左旋转、右旋转、双旋

 

1，LL ：– 右旋转（单旋）：为啥LL ，要用右旋转：LL 的意思是：左左，说明左边高度多了一个？

--------------------左边过重失衡，右旋转，把重量匀称一点到右边。

 

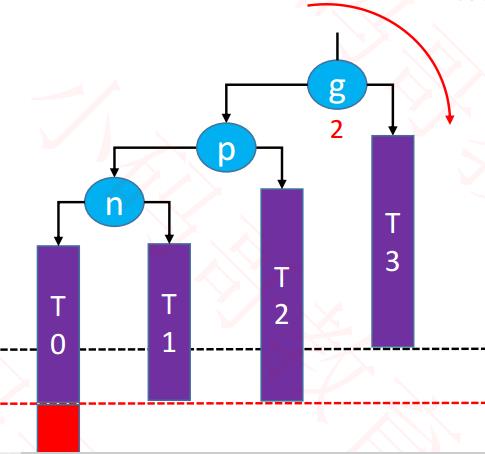
2，RR： – 左旋转（单旋）：为啥RR ，要用左旋转：RR 的意思是：右右，说明右边高度多了一个？

--------------------右边过重失衡，左旋转，把重量匀称一点到左边。

 

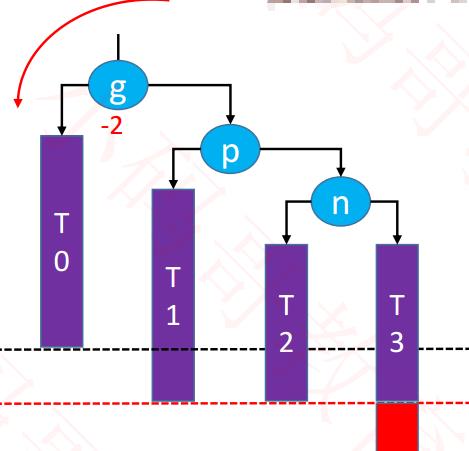
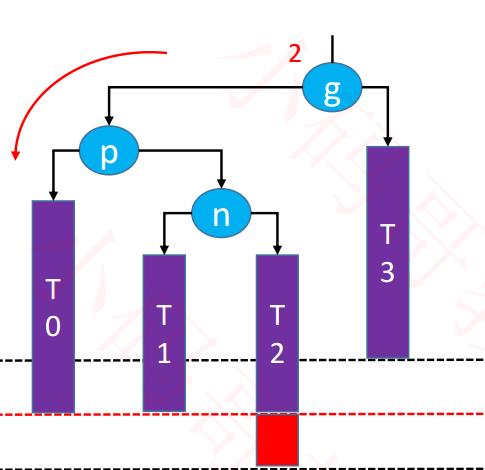
3，LR – RR：左旋转，然后得到 LL，再右旋转（双旋）：首先看LR-RR结构的最后一对是RR，

■ 为啥RR， 要用左旋转：RR 的意思是：右右，说明右边高度多了一个？

--------------------右边过重失衡，左旋转，把重量匀称一点到左边。

■ 然后得到LL，要用右旋转，LL的意思是：左左，说明左边高度多了一个？

--------------------左边过重失衡，右旋转，把重量匀称一点到右边。

　　　　　　

 

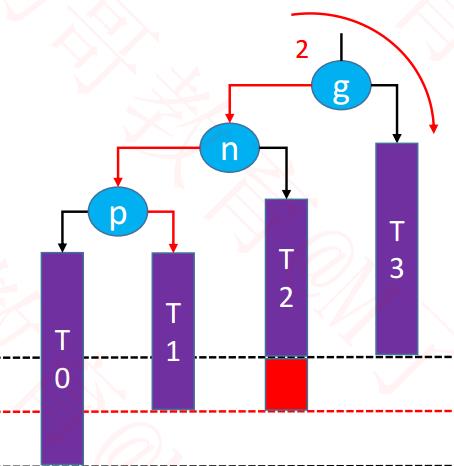
4，RL – LL：右旋转，然后得到 RR，再左旋转（双旋）：首先看RL-LL 结构最后一对是LL，

■ 为啥LL， 要用右旋转：LL 的意思是：左左，说明左边高度多了一个？

--------------------左边过重失衡，右旋转，把重量匀称一点到右边。

■ 然后得到RR，要用左旋转，RR的意思是：右右，说明右边高度多了一个？

--------------------右边过重失衡，左旋转，把重量匀称一点到左边。

　　　　　　

 

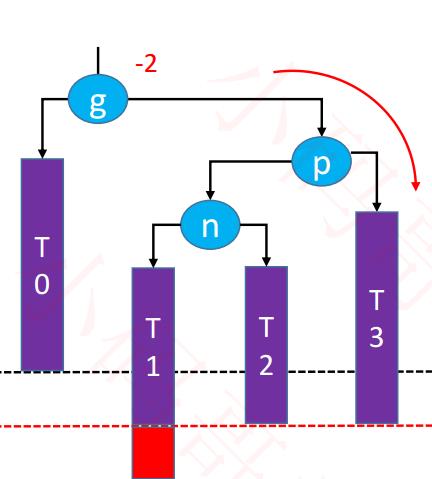
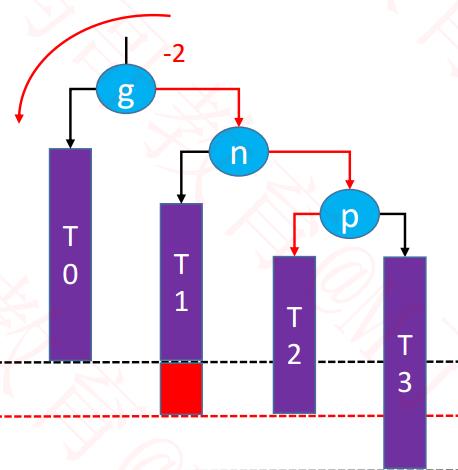
1、旋转的意义：就是为了匀称掉失衡的状态。 ✿ 最后一个字母就是提示失衡的情况： ● LL: 是左边失衡~ 右旋转 ● RR:是右边失衡~ 左旋转 ● LR-RR: （可以看到该结构最后一对是 RR，是右边失衡）左旋转，处理后得到~LL（是左边失衡），右旋转。 ● RL-LL：（可以看到该结构最后一对是 LL，是左边失衡）右旋转，处理后得到~RR（是右边失衡），左旋转。

红黑树实现

概念左旋转右旋转颜色反转插入节点过程设计架构

概念

• 节点是红色或黑色。

• 根节点是黑色。

• 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

• 每个Nil节点都是黑色

• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

左旋转

左旋转过程：

1            node                               x
2           /   \     左旋转                /  \
3          T1   x   --------->   node   T3
4              / \                         /   \
5             T2 T3                    T1   T2

---

 1/**
 2    Node<Key, Value>* leftRotate(Node<Key, Value> *node)
 3    {
 4        Node<Key, Value>* x = node->right;
 5        node->right = x->left;
 6        x->left = node;
 7
 8        x->color = node->color;
 9        node->color = Node::RED;
10        return x;
11    }

右旋转

右旋转过程：

1     node                         x
2    /   \     右旋转         /  \
3   x    T2   ------->   y   node
4  / \                             /  \
5 y  T1                         T1  T2

---

1    Node<Key, value>* rightRotate(Node<Key, Value>* node)
2    {
3        Node<key, Value> *x = node->left;
4        node->left = x->right;
5        x->right = node;
6
7        x->color = node->color;
8        node->color = Node::RED;
9        retu

颜色反转

 1/*
 2     *颜色反转
 3     *
 4     */
 5    void flipColors(Node<Key, Value>* node)
 6    {
 7        node->color = Node::RED;
 8        node->left->color = Node::BLACK;
 9        node->right->color = Node::BLACK;
10    }

插入节点过程

每次插入，跟二叉搜索树一样的递归过程，唯一多的功能是判断是否需要进行左旋转，右旋转或者颜色反转，最后需要一直保持根节点为黑色节点，过程如下图所示：

 1public:
 2    void add(const Key &k, const Value &v)
 3    {
 4        _root = add(_root, k, v);
 5        //最终根节点为黑色
 6        _root->color = Node::BLACK;
 7    }
 8private:
 9    /**
10     * 返回插入元素后红黑树的根
11     */
12        Node<Key, Value>* add(Node<Key, Value>* root, const Key &k, const Value &v)
13    {
14        if (root == nullptr)
15        {
16            _size++;
17            return new Node(k, v); 
18        }
19        if (k < root->key)
20        {
21            root->left = add(root->left, k, v);
22        }
23        else if(k > root->key)
24        {
25            root->right = add(root->right, k, v);
26        }
27        else
28        {
29            root->value = v;
30        }
31        // 左节点黑色，右节点红色
32        if (isRed(root->right) && !isRed(root->left))
33            root = rightRotate(root);
34        // 连续两个左子节点都是红色的，需要右旋转
35        if (isRed(root->left) && isRed(root->left->left))
36            root = rightRotate(root);
37         // 左右子树都是红节点，直接翻转颜色即可
38        if (isRed(root->left) && isRed(root->right))
39            flipColors(root);
40        return root;
41    }

设计架构

 1#ifndef __RBTREE_HPP
 2#define __RBTREE_HPP
 3//Author:Simon
 4//Email:[e-mail]
 5
 6template<typename Key, typename Value>
 7struct Node
 8{
 9    enum color { RED, BLACK };
10    Key key;
11    Value value;
12    int color;
13    Node *left;
14    Node *right;
15    Node(const Key &k,const Value &v):key(k),value(v),left(nullptr),right(nullptr),color(RED){}
16};
17
18template<typename Key,typename Value>
19class RBTree
20{
21public:
22    RBTree():_size(0),_root(nullptr);
23    ~RBTree();
24public:
25    void add(const Key &k, const Value &v);
26private:
27    Node<Key, Value>* leftRotate(Node<Key, Value> *node);
28    Node<Key, value>* rightRotate(Node<Key, Value>* node);
29    void flipColors(Node<Key, Value>* node);
30    bool isRed(Node<Key, Value>* node);
31    Node<Key, Value>* add(Node<Key, Value>* root, const Key &k, const Value &v);
32private:
33    int _size;
34    Node<Key, Value> *_root;
35};
36
37#endif // __RBTREE_HPP