机器学习 | EM算法与你所不知道的抛硬币案例

Posted 2021-04-03 AI算法词典

 关键词：机器学习 / EM / 估计

摘要： 

介绍 EM 的时候很多教程都喜欢用抛硬币的案例讲解流程，但殊不知这个案例潜藏着几个他们从来都没有提及的巨坑在其中，本篇文章就来细抠这些隐藏的部分，通过代码更好的理解 EM 算法！

 简介

EM算法的全名叫做 Expectation-Maximization 算法，是一种应用在目标函数没有办法直接被计算出来时统计模型，这个模型在1977年首次发表于一篇由三位作者合著的论文上：Arthur Dempster，Nan Laird，与 Donald Rubin。目标函数没有办法直接被计算出来的主要原因在于某些信息的丢失，当信息种类与未知参数种类数量不匹配的时候就容易发生这类情况，不过并非所有的这类情况都能通过 EM 算法解决，套用算法之前我们需要能够分辨哪一种类型的信息丢失可以适用 EM 算法。最常见的案例就是抛铜板的场景，在本篇文章中，我们将要详细解读 EM 算法与铜板问题的深度关系，除了探讨我们能够从算法的结果得出什么结论之外，我们还另外关注于算法的缺点与不足，通过构建一个专属于抛硬币案例的代码程序，我们能对更多的可能做一个完整的模拟，看到最后有一个 EM 算法的惊天结论，值得一读。

import numpy as np

如果还没有安装 numpy 的小伙伴，可以通过下面指令快速安装：

pip install numpy

 抛硬币案例

每个案例在最一开始之前都需要做一系列的假设，而抛硬币案例同样也不例外，这个假设至关重要：假设我们知道总共有多少个铜板，在下面的图示里一共假设铜板数量是两个，接着，有人抛了这些铜板 50 次，不过很不幸的是他并没有记录下每一次的正反结果是抛了哪一个铜板而得到的，这个情况就是本次案例中信息丢失的环节，在不知道这 50 次观测记录所对应铜板的情况下，我们的目标就是去计算每一个铜板翻到正面和反面的概率是多少，有一个非常经典的图示发布在 【the journal of Natrue Biotechnology, 26(8), 897】，它详细的讲述了 EM 算法求解过程的完整步骤，其中它把 50 次抛硬币的结果分成 5 个回合。

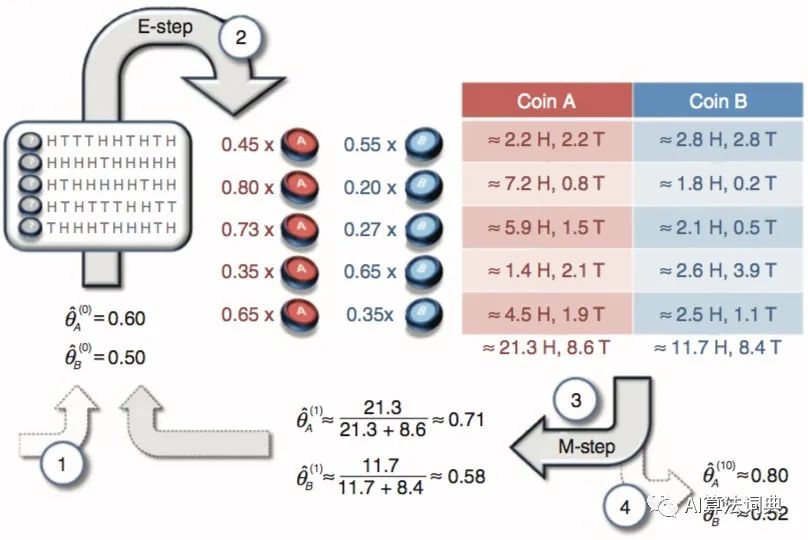
EM 算法顾名思义就是一个先求期望再求极大的算法，不断地循环往复就能逐渐逼近待求解问题的最优解，如上图所示，每一个数字代表着步骤的顺序：

1. 随机的初始化我们要求解的参数，也就是每一个硬币会抛到正面和反面的概率
2. 根据初始的概率和观测的结果，计算概率期望
3. 根据概率期望和拆分的不同回合，计算极大似然
4. 通过极大似然的计算结果，更新之前被随机假设的概率

不断地循环往复 2~4 个步骤，我们就能求出此概率的最优解。为了要用 Python 建模，首先第一步就是生成观测数据。

 第一步 - 数据生成

抛硬币案例的观测数据，也就是一系列的硬币结果需要根据两个假设来确定：

1. 确定每一个概率被选中用来抛的概率
2. 确定每一个硬币抛到正反面的概率

结合拆分观测序列成不同回合的功能，我们就能自己定义函数来生成观测结果。而这两个假设也将成为左右 EM 算法结果的关键要素，细节将在下面深入讲解。

def norm(arr):
    return np.array(arr) / np.sum(arr)

def gen_obs(n_sequence, n_sample, probs_H, weights):
    tot = n_sample * n_sequence
    probs_H = np.array(probs_H)
    weights = norm(weights)
    n_h = int(tot * np.sum(probs_H * weights))
    obs = np.hstack([np.ones(n_h), np.zeros(tot - n_h)])
    np.random.shuffle(obs)
    return obs.reshape(n_sequence, n_sample)

gen_obs(5, 10, [0.6, 0.5], [0.5, 0.5])

输出：
[[1., 0., 1., 1., 1., 0., 1., 0., 1., 1.],
 [0., 0., 0., 1., 0., 1., 0., 0., 0., 1.],
 [1., 1., 0., 1., 1., 1., 0., 1., 1., 1.],
 [1., 1., 1., 1., 0., 1., 0., 0., 0., 0.],
 [0., 0., 1., 0., 0., 1., 1., 0., 0., 1.]]

其中 1 表示正面，而 0 则表示反面，在本次观测值生成中，我们假定有两个硬币，每个硬币被选中用来抛的概率是一样的 50%，每个硬币翻到正面的概率分别是 60% 与 50%，由于硬币只有两面，知道了正面的概率就同样知道反面的概率，不过为了和图例中的观测结果一致，我们这里另外定义了一个观测结果。

obs = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1],
                [1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
                [1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
                [1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
                [0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])

 第二步 - 求期望

如同我们最一开始强调的假设，在使用 EM 算法前我们需要知道一共有多少个硬币参与其中，如果我们不知道一共有多少个，但是又想用 EM 算法求解，那我们只能自行假设我们知道他是... 例如3个(纯粹脑补的结果)，沿着标注了数字的箭头：

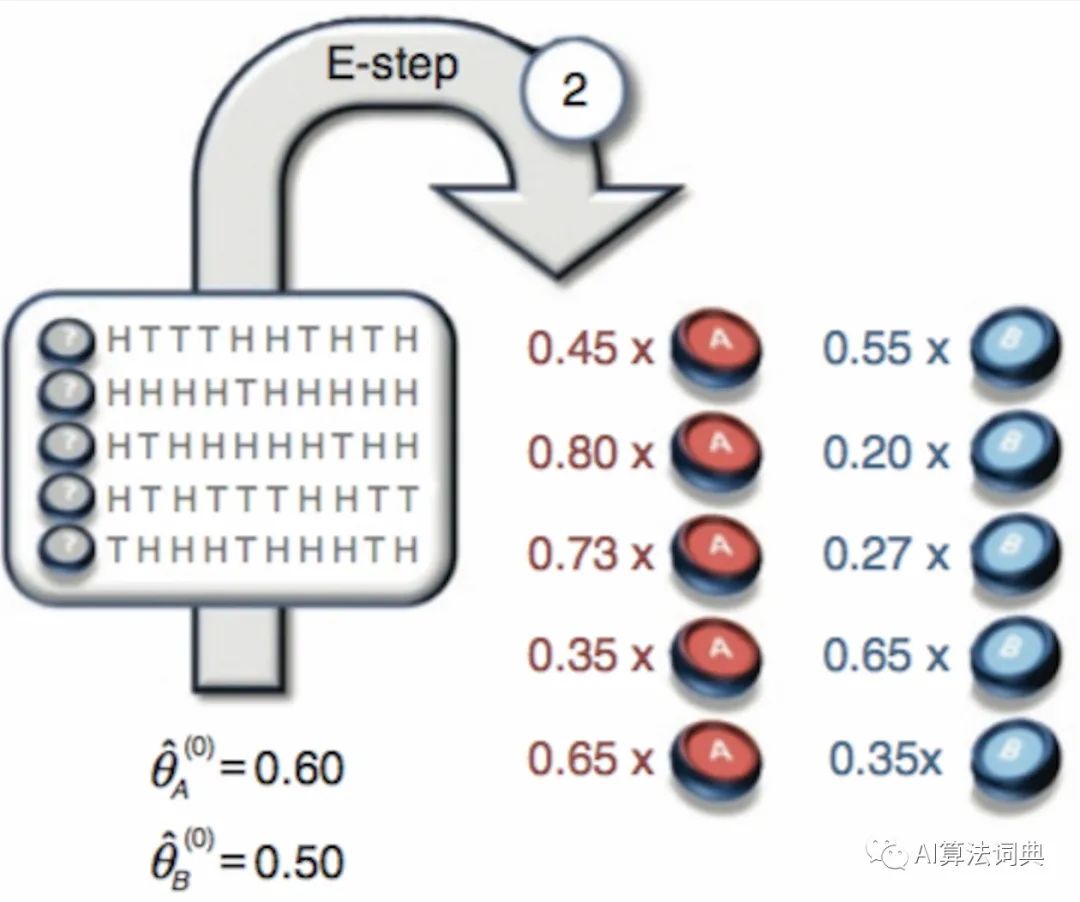
首先就是猜概率 ( 与 ) 分别对应 A 硬币与 B 硬币抛到正面的概率。由于硬币问题是一个二项分布，结合观测结果与二项分布的计算方法，正反面的次数放平方的位置，正反面的概率作为被平方的值，我们得到如下结果：

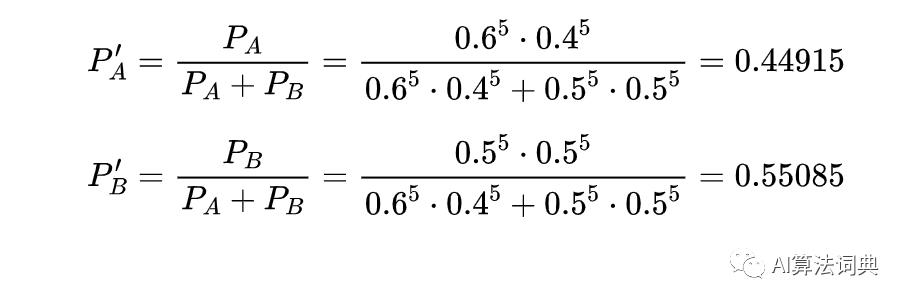
同样方法可以计算这五个回合，用代码可以写成：

def E_step(obs, probs_H):
    # 根据二项分布计算概率的次方 ...
    pow_H = np.tile(np.sum(obs == 1, axis=1), (len(probs_H), 1)).T
    # ... 并把结果复制成对应的矩阵尺寸
    pow_T = np.tile(np.sum(obs == 0, axis=1), (len(probs_H), 1)).T
    # 每一个观测回合都假设是遵循着同样的正反概率
    probs_H = np.tile(probs_H, (len(obs), 1))

    # 估计选到每一个铜板的期望
    expectation = np.power(probs_H, pow_H) * np.power(1 - probs_H, pow_T)
    # 将结果归一化到 0 和 1 之间
    expectation /= np.sum(expectation, axis=1).reshape(-1, 1)
    return expectation

exp = E_step(obs, [0.6, 0.5])
print(exp)

输出:
[[0.44914893 0.55085107]
 [0.80498552 0.19501448]
 [0.73346716 0.26653284]
 [0.35215613 0.64784387]
 [0.64721512 0.35278488]]

 第三步 - 求极大

接下来，我们假设期望概率对于每一个硬币是一个真实结果 (数量单位)，我们就能统计出在这所有回合里，硬币出现正反面的次数占所有数量的比例关系，在第一个观测回合中，一共有5个正面和5个反面

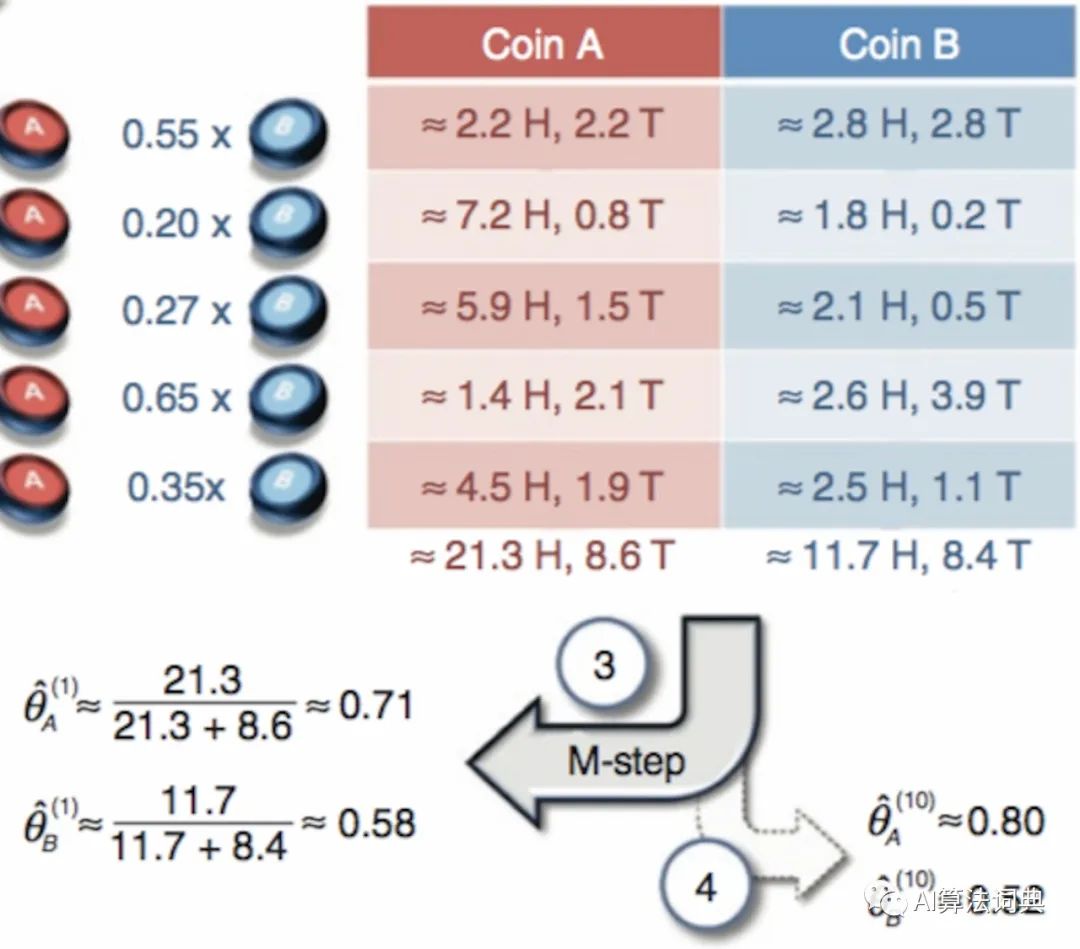
对应的计算过程如下：

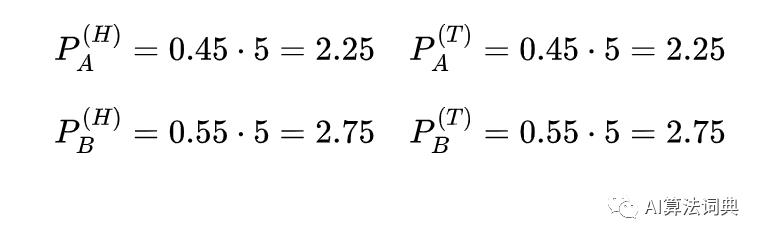
把所有观测回合的这些计算结果加总起来，我们就能得到每个硬币在不同情况下新的统计值，而这些值将能够被进一步用来计算每个硬币对应不同情况的概率。

def M_step(obs, exp):
    # 根据期望数一数新的正反面硬币 "数量"
    cnt_H = exp * np.sum(obs == 1, axis=1).reshape(-1, 1)
    cnt_T = exp * np.sum(obs == 0, axis=1).reshape(-1, 1)
    # 计算正反面的总数，作为分母
    tot_H = np.sum(cnt_H, axis=0)
    tot_T = np.sum(cnt_T, axis=0)
    return tot_H / (tot_H + tot_T)

probs_new = M_step(obs, exp)
print(probs_new)

输出:
[0.71301224 0.58133931]

经过一通计算，向量里的结果与图示中的结果一摸一样，表示我们建模过程的正确性。

细究硬币案例

虽然所有步骤表面上看起来都在正确的轨道上运行着，但别忘了能够顺利运行的背后存在着大量的前提假设：

1. 参与抛掷的硬币数量
2. 每个硬币被选中的概率

而这些假设正是让 EM 算法的结果非常不稳定的主要原因，有时候即便这两个假设产生的观测值有着比较明显的特征，求解的过程还是容易陷入到局部最优解中，导致结果离真实解还有一段明显的距离。

def EM(init=[0.3, 0.9], hidden=[0.7, 0.5]):
    tries = []

    for _ in range(10):
        obs = gen_obs(100, 10, hidden, [0.5, 0.5])

        # Initialize the probabilities
        estimated_H = np.array(init)

        for _ in range(1000):
            expectations = E_step(obs, estimated_H)
            estimated_H = M_step(obs, expectations)

        tries.append(estimated_H)

    return np.array(tries)

print(EM([0.3, 0.9], [0.7, 0.5]))

输出:
[[0.53260284 0.6668931 ]
 [0.50093282 0.6976262 ]
 [0.6        0.6       ]
 [0.6        0.6       ]
 [0.6        0.6       ]
 [0.6        0.6       ]
 [0.53018209 0.67072691]
 [0.6        0.6       ]
 [0.56819878 0.63177121]
 [0.6        0.6       ]]

在上面代码模拟的情况里，我们假设一共有两个硬币，每个硬币有同样的概率被选中用来抛掷，我们希望 EM 算法能够求解出 hidden probabilities [0.7, 0.5]，也就是每个硬币翻到正面的概率，然而根据实验结果来看，虽然偶尔 EM 算法能够估计正确，但两个 0.6 的概率看起来更像是一个好的选择，这也是合情合理的，因为根据 0.7 与 0.5 概率生成出来的随机观测结果，如果拿来跟 0.6 与 0.6 概率生成出来的随机观测结果一对比就会发现它们之间基本没什么区别，类似的情况在不同概率假设的实验中也能有所体现，因此我们没办法要求 EM 算法在如此接近的观测值中给出非常精确且一致的解，这也是解释为什么 EM 算法容易陷入局部最优的有力理由，甚至我们只要简单变一下假设：

• 假设每一个铜板被选中用来抛掷的概率不一致

那么 EM 算法基本就可以缴械投降了，因为这等于基于一个信息已丢失的状态，进一步丢失了更多的信息，每次估计出来的结果也就离真实概率天差地远，所以从多次试验表明，抛硬币问题并不能很好的被 EM 算法求解，只能说能被它估计。

print(EM([0.3, 0.9], [0.7, 0.6]))

输出:
[[0.57684374 0.72123039]
 [0.5890758  0.70904314]
 [0.58458891 0.7127802 ]
 [0.57718465 0.72154361]
 [0.649      0.649     ]
 [0.649      0.649     ]
 [0.649      0.649     ]
 [0.61382089 0.68415056]
 [0.649      0.649     ]
 [0.649      0.649     ]]

此外，如果我们调整一下铜板的隐藏概率给 EM 算法求解，同样发现结果还是会有 "对半分" 的估计在里面，不过好处是这次有更多次的估计是更成功的，主要原因就在于 0.7 与 0.6 概率生成出来的观测序列更有特征，明显正面结果在总共结果中是主要优势，并且两个铜板对正面结果都有比较多的贡献，相较于前面的 0.7 与 0.5 而言也就多了几分确定性在里面，所以预测的结果就能更好一些！

 结论

EM 算法很酷的地方在于它能够在某些信息丢失的情况下还能估计出我们想知道的概率，然而很多假设必须提前被确定下来，造成了许多 "巧合" 可能会发生在整个计算的过程当中，例如估计结果对半分的情况就是一个典型案例。从数学的角度来说这些巧合则以局部最优的结果呈现，局部最优的问题无从避免，除非我们能适当的调整一下隐变量的值，像调整 0.7, 0.5 成 0.7, 0.6 的操作稍稍缓解了一点局部最优的问题，但问题在于隐变量正是我们要求的东西，是不能拿来随意调整的，因此局部最优的问题总是无时不刻的伴随着 EM 算法在各个领域的应用。

 End

---

清华大学，数据科学与信息技术，研究生在读

#征 稿 啦#

 分享属于你的idea 

AI算法词典为大家提供一个开放的交流平台，

鼓励高校实验室或个人，

积极在我们的平台上分享各种高质量的内容，

这些内容可以是最新的论文解读、学习经验或技术干货。

以上是关于机器学习 | EM算法与你所不知道的抛硬币案例的主要内容，如果未能解决你的问题，请参考以下文章

你所不知道的文本挖掘

你所不知道的贪心算法

机器学习EM算法

机器学习EM算法

《你所不知道的：大神与一般程序猿的区别》读书笔记

机器学习 | 深入理解EM算法