十一.聚类算法

Posted 2021-04-03 AceYA

一.聚类算法简介

1.概念

        一种典型的无监督学习算法。根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

2.应用

        用户画像，广告推荐，新闻聚类，图像分割。

3.分类

        粗聚类，细聚类

4.聚类方法

• 划分式聚类方法 k-means，k-means++，bi-kmeans
• 基于密度的聚类方法 DBSCAN，OPTICS
• 层次化聚类方法 Agglomerative，Divisive
• 新方法 量子聚类，核聚类，谱聚类

二.聚类算法实现流程----k-means

1.k-means包含两层内容：

• K：初始中心点个数（计划聚类数）
• means：求中心点到其他数据点的距离的平均值

2.k-means步骤

1. 随机设置k个特征空间内的点作为初始聚类的中心
2. 计算其他每个点到k个中心的距离，距离最近的一些点标记为一类，最后分成k类
3. 对标记后的k个聚类，分别计算每个聚类的新中心点
4. 如果新中心点与原中心点一样便结束，否则重新进行第二步（新中心点和上一步中心点有一个差值阈值）

比如下图：

三.聚类算法API----k-means

sklearn.cluster.KMeans(n_clusters=8)
    '''
    参数:
     n_clusters:开始的聚类中心数量
      整型，默认为8，生成的聚类数，即要把数据集分成几类。
    方法:
     KMeans.fit(x)   # 模型训练
     KMeans.predict(x)  # 输出预测值
     KMeans.fit_predict(x) # 综合，训练模型并输出类别标签结果
    '''

示例：

    #0.导入工具库
    '''
    samples_generator生成数据
    calinski_harabasz_score评估结果，值越大分类结果越好
    '''
    import matplotlib.pyplot as plt
    from sklearn.datasets.samples_generator import make_blobs
    from sklearn.cluster import KMeans
    from sklearn.metrics import calinski_harabasz_score
    
    #1.获取数据，2.数据基本处理，3.特征工程
    X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],cluster_std=[0.4, 0.2, 0.2, 0.2],random_state=9)
    '''
    参数
     n_samples:要生成多少个数,默认100
     n_features：数据维数,x的维度，默认为2不可更改
     centers：int类型，数据有几个中心点，即数据的种类数，默认为3；也可以用二维数组自定义几个具体的点
     cluster_std：int类型，每个中心点与周围数据点的标准差，注意要与centers个数相同
     return_centers：bool,默认false，为true时返回centers
    返回值
     X：二维数组
     y:每个数据点的类别标签值,总共n_samples个
     centers:中心点的坐标，return_centers=True时返回
    '''
    
    # 数据集可视化
    plt.scatter(X[:, 0], X[:, 1], marker='o')
    plt.show()
    '''见图1'''
    
    #4.模型训练，5.模型评估
    y_pred = KMeans(n_clusters=2, random_state=9).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.show()
    # 用Calinski-Harabasz Index评估的聚类分数
    print(calinski_harabasz_score(X, y_pred))#3116.1706763322227
    '''见图2'''
    
    y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.show()
    print(calinski_harabasz_score(X, y_pred))#2931.6250301995556
    '''见图3'''
    
    y_pred = KMeans(n_clusters=4, random_state=9).fit_predict(X)
    plt.scatter(X[:, 0], X[:, 1], c=y_pred)
    plt.show()
    print(calinski_harabasz_score(X, y_pred))#5924.050613480169
    '''见图4'''

图1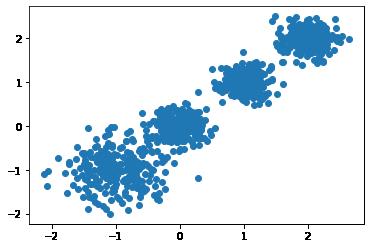

图2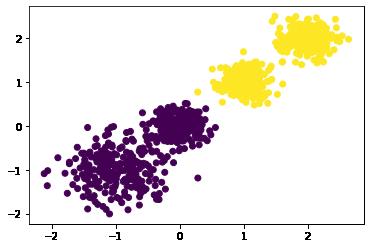

图3

图4

四.模型评估

1.误差平方和(SSE The sum of squares due to error)

        误差平方和的值越小越好

2 “肘”方法 (Elbow method) — K值确定

        下降率突然变缓时即认为是最佳的k值

3 轮廓系数法（Silhouette Coefficient）

        取值为[-1, 1]，其值越大越好

4 CH系数（Calinski-Harabasz Index）

        分数s高则聚类效果越好。类别内部数据的协方差越小越好，类别之间的协方差越大越好。

        CH需要达到的目的：用尽量少的类别聚类尽量多的样本，同时获得较好的聚类效果。

五.其他聚类算法

K-means优缺点

优点

• 原理简单（靠近中心点），实现容易
• 聚类效果中上（依赖K的选择）
• 空间复杂度o(N)，时间复杂度o(IKN)

缺点

• 对离群点，噪声敏感 （中心点易偏移）
• 很难发现大小差别很大的簇及进行增量计算
• 结果不一定是全局最优，只能保证局部最优（与K的个数及初值选取有关）

优化方法	思路
Canopy+kmeans	Canopy粗聚类配合kmeans
kmeans++	距离越远越容易成为新的质心
二分k-means	拆除SSE最大的簇
k-medoids	和kmeans选取中心点的方式不同
kernel kmeans	映射到高维空间
ISODATA	动态聚类，可以更改K值大小
Mini-batch K-Means	大数据集分批聚类

六.案例

        应用pca和K-means实现用户对物品类别的喜好细分划分