数据结构栈的操作

Posted 2021-10-14 主教主

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构栈的操作相关的知识，希望对你有一定的参考价值。

栈

定义：栈是限定仅在表尾进行插入或删除操作的线性表。

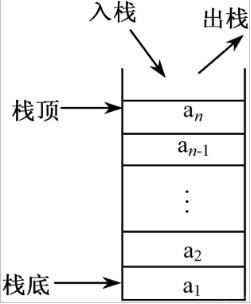
由于栈只有一边开口存取数据，称开口的那一端为“栈顶”，封死的那一端为“栈底”（类似于盛水的木桶，从哪进去的最后还得从哪出来）。

栈操作数据元素的方法

栈操作数据元素只有两种动作：

入栈：在栈顶插入一个元素的操作；
出栈：从栈顶删除一个元素的操作；

栈的“先进后出”原则（Last In First Out）

使用栈存储数据元素，对数据元素的“存”和“取”有严格的规定：数据按一定的顺序存储到栈中，当需要调取栈中某数据元素时，需要将在该数据元素之后进栈的先出栈，该数据元素才能从栈中提取出来。

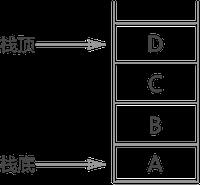
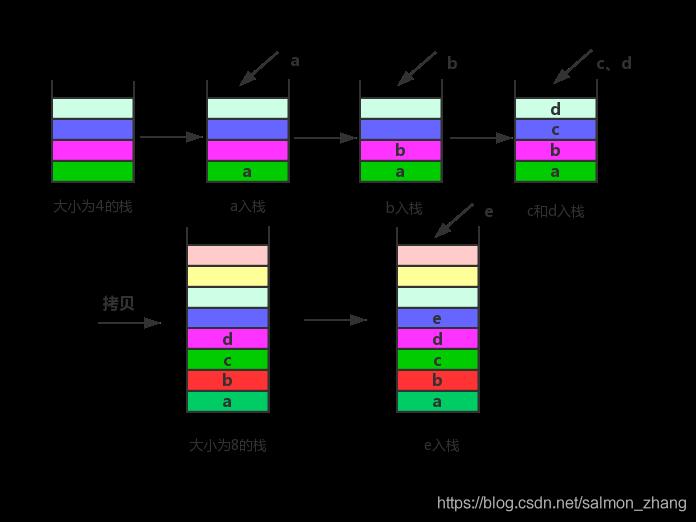
如图 1 ，栈中存放了 4 个数据元素，进栈的顺序是 A 先进栈，然后 B 进，然后 C 进，最后 D 进栈；当需要调取 A 时，首先 D 出栈，然后 C 出栈，然后 B 出栈，最后 A 才能出栈被调用。

就好比只有一个门的车库（每次仅允许一辆车通过），每辆车好比一个数据元素，只有离门最近的车先开出来，里边的车才能出来；最里边的车是最先开进去的，注定要最后出来。

栈的表示和实现

既然栈也是线性表，那么它就同样有线性表的两种表示形式：顺序栈和链式栈（简称“链栈”）。

栈的顺序存储结构（顺序栈）

顺序栈：是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。

#define MAXSIZE 100    /*  栈的最大容量 */
typedef int ElemType;     /*元素类型*/
/* 顺序栈 */
typedef struct{ 
	SElemType data[MAXSIZE];
	int top; //栈顶指针 ,约定指向栈顶元素的下一个位置
} SqStack;

顺序栈的算法实现

初始化空栈

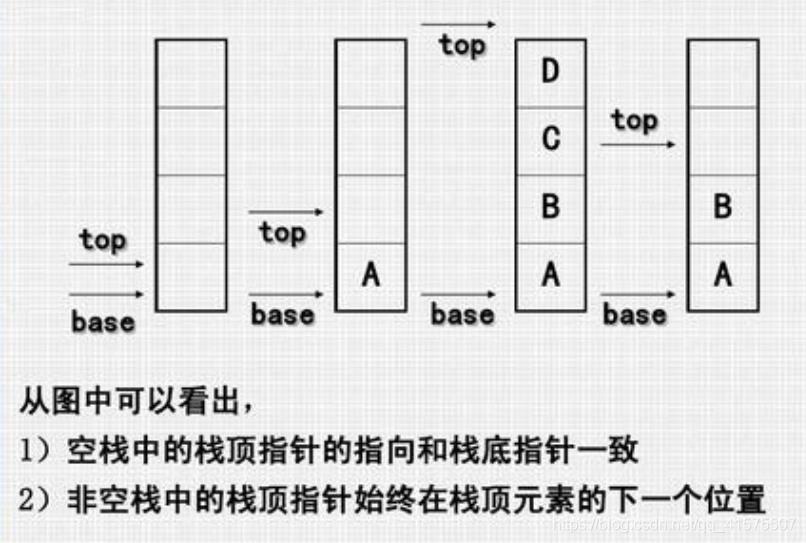
约定：非空栈的栈顶指针top始终指向栈顶元素的下一个位置.

void initSqStack(SqStack *s)
{
	s->top= 0;

}

### 判断栈空

bool isEmptyStack(SqStack s)
{
	if (s.top==0)      				//栈顶指针应该指向栈顶元素的下一个位置，否则栈空。
	return true;
	else
	return false;
}

入栈

bool push(SqStack s,SElemType e) / s指向栈的指针变量，指针作为参数，可以将变化后的栈的值传递出来 /
{
	if (s->top >=MAXSIZE)
		return false;
	else
 {
	s->data[s->top]=e; //先插入，
	s->top ++; //栈顶指针后加1
	//相当于 s->data[s->top++]
		return true;
 }
}

出栈

bool pop(SqStack *s,SElemType *e) /* 指针作为参数，可将修改后的值传递出来 */
{
  if (s->top ==0)
        return false ;
  else
  {

       --s->top;            //栈顶指针先减1
	   *e=s->data[s->top];  //再读取删除元素
       //*e=s->data[--s->top ];   //等价
      return  true;
  }

}

读栈顶

SElemType getTop(SqStack s)
{
  SElemType e;
  if (s.top ==0)
        return false ;
  else
  {
      e=s.data[s.top-1];
      return e;
  }

}

注意：上面的顺序栈是静态栈，空间一旦定下就难改而且一旦没有一段连续的内存，就会申请失败
那么，就出现了动态顺序存储栈，代码附下：

点击查看代码

#include <stdio.h>
#include <stdlib.h>
#define TURE 1
#define FALSE 0
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
typedef int SelemType;
/*---动态分配栈--*/
typedef struct
{
    SelemType *base;
    SelemType *top;
    int StackSize;
} SeqStack;
/*---初始化---*/
int InitStack(SeqStack *s)
{
    s->base = (SeqStack *)malloc(STACK_INIT_SIZE*sizeof(SeqStack));
    if(!s->base)
        printf("创建失败");
    else
    {
        s->top = s->base;
        s->StackSize = STACK_INIT_SIZE;
    }
}
/*---判断栈是否为空---*/
int IsEmpty(SeqStack *s)
{
    if(s->top==s->base)
    {
        return TURE;
    }
    else
    {
        return FALSE;
    }
}

/*---入栈操作---*/
int push(SeqStack *s,SelemType x)
{
    if((s->base)-(s->base)==s->StackSize)
    {
        s->base = (SeqStack *)realloc(s->base,(s->StackSize+STACKINCREMENT)*sizeof(SeqStack));
        if(s->base==NULL)
        {
            return FALSE;
        }
        s->top  =s->base+s->StackSize;
        s->StackSize +=STACKINCREMENT;
    }
    else
    {
        *s->top = x;
        s->top++;
        return(TURE);
    }
}
/*---出栈操作---*/
int Pop(SeqStack *s,SelemType *x)
{
    if(s->top==s->base)
    {
        return FALSE;
    }
    else
    {
        s->top--;
        *x = *s->top;
        return (TURE);

    }
}

链式存储结构（链式栈）

链栈，用线性表的链式存储结构实现。
用链表表示栈时，用链表头结点的一端作为栈的栈顶端，这样做的好处是当数据元素压栈或者弹栈时，直接使用头指针就可以完成，不需要增设额外的指针。

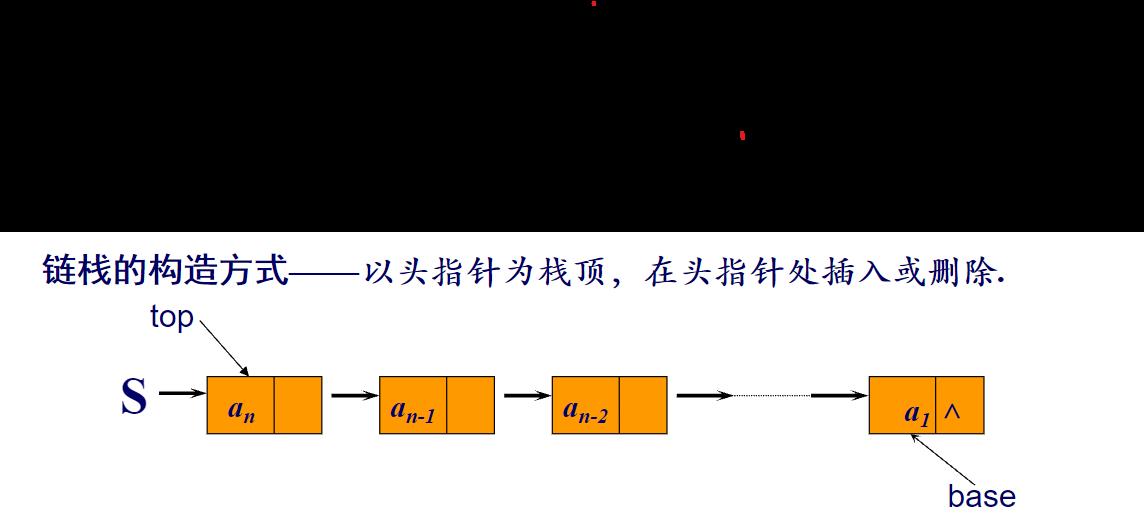
typedef Struct SNode{
    ElemType  data;
    Struct   SNode   * next;
 } SNode;

栈的应用举例

数制的转换（以8进制为例）

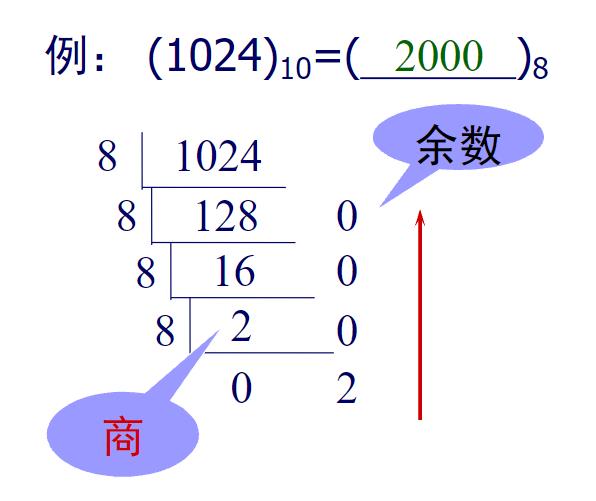
void conversion(int n)
{
   SqStack s;
   ElemType e;
   bool tmp;
   initSqStack(&s);
   while(n)
  {
     tmp=push(&s,n%8);   /* 求余数压栈 */
     n=n/8;
   }
   while(!isEmptyStack (s))
   {
       tmp=pop(&s,&e);
       printf("%3d",e);

   }
   printf("\\n");
}

算术表达式求值

一个表达式由操作数、运算符和界限符组成。

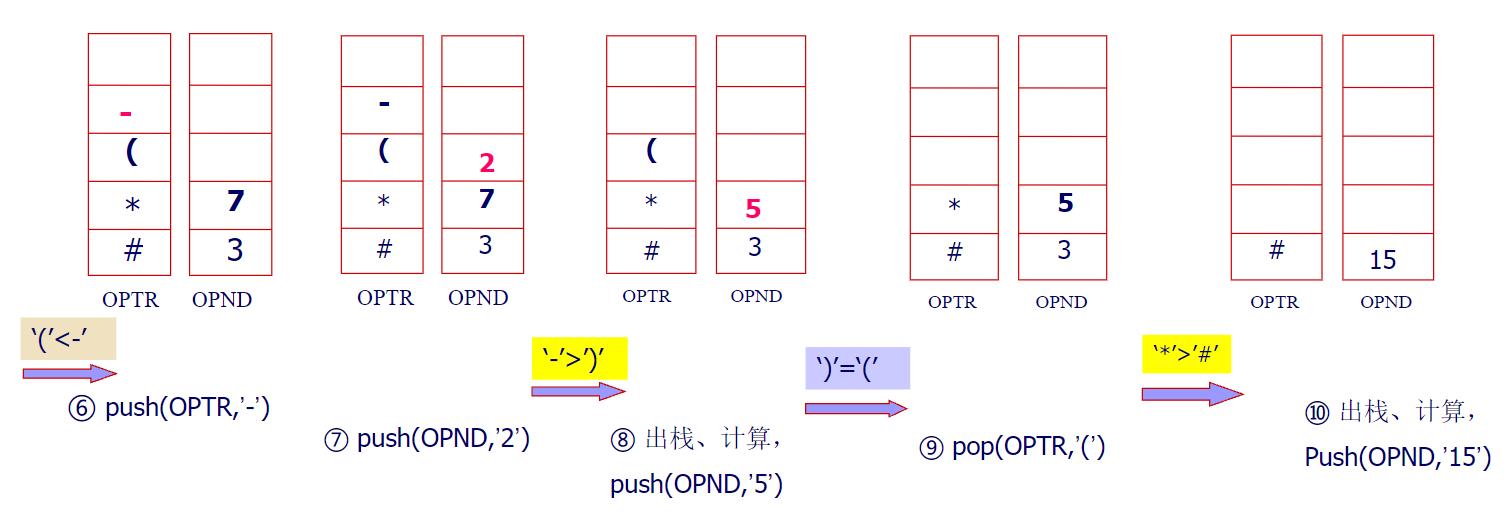
伪代码：

OprandType EvaluateExpression( ){
    InitStack(OPTR); PUSH(OPTR,’#’);
    InitStack(OPND); c=getchar();
    While(c!=‘#’||GetTop(OPTR)!=‘#’){
        If(!In(c,op)) {PUSH(OPND,c);c=getchar();}    //In(c,op)       C是运算符吗？
        Else
           switch(Precede(GetTop(OPTR) ,  c )){
              case ‘<’   PUSH(OPTR,c);c=getchar();break;
              case ‘=’   POP(OPTR,x);c=getchar();break;
              case ‘>’   POP(OPTR,theta); 
                         POP(OPND,b); POP(OPND,a);              
                         PUSH(OPND,operate(a,theta,b));
                         break;
          }//switch
     }//while
}//EvaluateExpression

括号的匹配问题（具体在博客另一篇随笔）

数据结构栈的简单理解和基本操作

前言：本章介绍的主要内容是数据结构中栈的概念和栈的基本操作，包括：栈结构的定义、初始化、容量检查、判空、入栈、出栈、读取栈顶元素、读取栈内元素个数、栈的销毁等操作的具体实现。

文章目录

1.为什么需要栈？

1.1栈的概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。**进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。**栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈，出数据也在栈顶。

2.栈项目文件搭建

程序名	功能
`Stack.h`	定义结构体,引头文件,函数的声明
`Stack.c`	各个功能函数的定义
`test.c`	测试函数功能

栈的基本操作主要有：栈的初始化、判空、判满、取栈顶元素、在栈顶进行插入和删除，后下文将逐一实现。在栈顶插入元素称为入栈，在栈顶删除元素称为出栈。

2.1 栈结构的代码实现

typedef int STDataType;  

typedef struct Stack
{
    STDataType* data; //接收动态开辟的数组地址
    int top;      //栈顶
    int capacity; //容量
}ST;

2.2 栈的初始化

就是初始化成空栈，把 data指针置为NULL, top和capacity初始化为0.

void StackInit(ST* ps)   
{
    assert(ps); //传进来的地址一定不能为空
    
    ps->data = NULL;
    ps->top = ps->capacity = 0;
}

2.3 栈的检查容量操作

当我们使一个元素入栈的之前，我们往往需要判断一下栈是否为满栈，防止发生上溢的情况。

提问：怎么判断容量满了呢?

答案:ps->top == ps->capacity.

void StackCheckCapacity(ST* ps)
{
    assert(ps);  //ps不可为空
    
    if(ps->top == ps->capacity)
    {
        //注意细节，如果此时容量为0,就给4个,否则就翻倍
        int newcapacity = (ps->capacity == 0 ? 4 : 2 * ps->capacity ); 
        
        STDataType* newdata = (STDataType*)realloc(ps->data,newcapacity*sizeof(STDataType));
        
        if(newdata == NULL)
        {
            perror("错误原因:");
            exit(-1);
        }
        ps->data = newdata; //重新交接给ps->data
        
        ps->capacity = newcapacity;
    }
}

2.4 栈的判空操作

当我们弹出栈顶元素时，往往需要判断一下栈是否为空来防止发生下溢。

void StackPush(ST* ps,STDataType elem)
{
    assert(ps); //ps不能为空
    
    return ps->top == 0; //等于0就返回1,
}

2.5 栈的入栈操作

入栈时我们首先要判断栈是否为满栈，如果为满栈我们要首先追加存储空间，然后才能将元素入栈。

void StackPush(ST* ps,STDataType elem)
{
    assert(ps); 
    
    StackCheckCapacity(ps); //检查容量是否满了
    
    ps->data[ps->top++] = elem;
}

2.6 栈的出栈操作

出栈时我们首先要判断栈是否为空栈,然后只需要ps->top减去1就行。

void StackPop(ST* ps)
{
    assert(ps);
    
    assert(!StackEmpty(ps));
    
    ps->top--;
}

2.7 栈的读取元素数量操作

直接把ps->top的值返回

size_t StackSize(ST* ps)
{
    assert(ps);
    
    return ps->top;
}

2.8 栈的读取栈顶操作

直接通过ps->top-1把值返回

STDataType StackTop(ST* ps)
{    
	assert(ps);        
	assert(!StackEmpty(ps));        
	return ps->data[ps->top - 1];
}

2.9 栈的销毁操作

直接free

void StackDestroy(ST* ps)
{    
	assert(ps);    
	free(ps->data);
	//当ps->data是NULL时候,free什么都不会做    
	ps->data = NULL;    
	ps->top = ps->capacity = 0;
}

3.源码链接

栈的代码实现

数据结构的栈内容到此设计结束了，感谢您的阅读！！！如果内容对你有帮助的话，记得给我三连（点赞、收藏、关注）——做个手有余香的人。

以上是关于数据结构栈的操作的主要内容，如果未能解决你的问题，请参考以下文章

Android Studio - 带回栈的导航抽屉

数据结构&算法08-栈概念&源码